فصل ۷ بنگاه اقتصادی و مشتریان آن
فهرستها و موضوعات فصلها
یک بنگاه اقتصادی با سود حداکثری که یک محصول متمایز را تولید میکند، چگونه با مشتریان خود تعامل میکند؟
- بنگاههای اقتصادیی که کالاهای متمایز تولید میکنند، با در نظر گرفتن منحنی تقاضای محصول و تابع قیمت، قیمت و کمیت را طوری تعیین میکنند که سودشان را به حداکثر برساند.
- مزیت فناورانه و مزیت قیمتیای که تولیدکنندگان کلان مقیاس از آنها برخوردارند، به نفع بنگاههای اقتصادی بزرگ است.
- پاسخ مشتریان به یک تغییر قیمتی، براساس خاصیت کشسانی تقاضا اندازهگیری میشود که حاشیه قیمتی و سود بنگاه اقتصادی را تحت الشعاع قرار میدهد.
- عواید حاصل از دادوستد و تجارت میان مصرفکنندگان و مالکان بنگاههای اقتصادی تقسیم میشود، اما قیمتهای بالاتر از هزینه نهایی موجب شکست بازار و خسارت سنگین میشوند.
- بنگاههای اقتصادی میتوانند با انتخاب و تبلیغات سودشان را بالاتر ببرند، آنهایی که رقبای کمتری دارند میتوانند حاشیه سود بالاتر و بهره انحصاری بدست بیاورند.
- سیاست گذاران اقتصادی با استفاده از کشسانیهای تقاضا، خط مشیهای مالیاتی را طراحی میکنند و قدرت بازاری بنگاه اقتصادی را با خط مشی رقابتی کاهش میدهند.
کتاب کوچک زیباست ارنست اف.شوماخر در سال ۱۹۷۳ منتشر شد و از تولید خرد-مقیاس توسط افراد و گروهها دربطن یک نظام اقتصادی دفاع میکرد که به جای تأکید بر سود برای تأکید بر خوشبختی طراحی شده بود.1 در سالی که کتاب منتشر شد، شرکتهای اینتِل (Intel) و فِداِکس (FedEx) هر کدام تنها چند هزار نفر کارمند در آمریکا داشتند، اما چهل سال بعد اینتل حدود ۱۰۸۰۰۰ نفر و فداکس بیش از ۳۰۰۰۰۰ نفر را را استخدام کردند. کمپانی والمارت هم که در سال ۱۹۷۳ تنها ۴۵۰۰ کارمند داشت در سال ۲۰۱۴ تعداد ۲.۳ میلیون نفر را به استخدام خود در آورد.
غالب بنگاههای اقتصادی بسیار کوچک تر از این هستند اما تقریباً در همه اقتصادهای ثروتمند، بیشتر مردم برای بنگاههای اقتصادی بزرگ کار میکنند. در ایالات متحده نیمی از کارکنان بخش خصوصی در بنگاههای اقتصادیی کار میکنند که حداقل ۱۰۰۰ کارمند دارند. بنگاه اقتصادی ها بهاین دلیل رشد میکنند که مالکان بنگاههای اقتصادی از بزرگ شدن آنها سود میبرند و افرادی که پول برای سرمایه گذاری دارند هم با تملک اجناس بنگاههای اقتصادی بزرگ بازگشت بیشتری از پولشان بدست میآورند. کارکنان هم در بنگاههای اقتصادی بزرگ بیشتر حقوق میگیرند. شکل ۷.۱ رشد برخی از بنگاههای اقتصادی بسیار موفق آمریکایی را نشان میدهد:
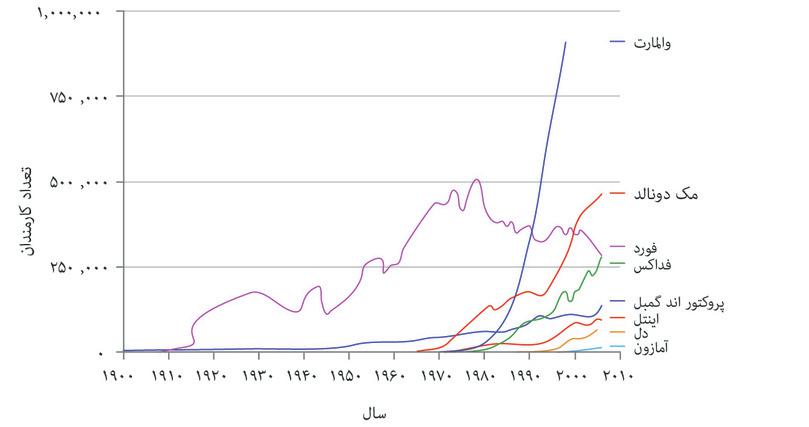
اندازه بنگاههای اقتصادی در ایالات متحده: تعداد کارکنان (۱۹۰۰ تا ۲۰۰۶)
شکل ۷.۱ اندازه بنگاههای اقتصادی در ایالات متحده: تعداد کارکنان (۱۹۰۰ تا ۲۰۰۶)
Erzo G. J. Luttmer. 2011. ‘On the Mechanics of Firm Growth’. The Review of Economic Studies 78 (3): pp. 1042–68.
بنگاههای اقتصادی برای اینکه مثل بنگاههای اقتصادی شکل ۷.۱ رشد کنند، چه راهبردهایی را باید اتخاذ کنند؟ داستان خرده فروشی تِسکو (Tesco) که تقریباً یک قرن پیش توسط جک کوهن تأسیس شد، پاسخی را به ما پیشنهاد میکند.
جک کوهن بنیانگذار تسکو کار حرفهایاش را بعنوان یک دلال بازاری خیابانی در محلات شرقی لندن آغاز کرد. دلالها رأس طلوع آفتاب در نقطهای کنار هم جمع میشوند و با صدای سوت به طرف محل موردعلاقه شان برای کاسبی کردن که به آن بساط میگویند هجوم میبرند. کوهن برای تصاحب مطلوبترین محل بساط، پیش از سر رسیدن دیگران کلاهش را پرت میکرد و در این فن سرآمد بود. اولین فروشگاههای تسکو تقلیدی از همین بساطها بود و هیچ دری نداشت. اما در دهه ۱۹۵۰ کوهن شروع کرد به اینکه فروشگاههایی به سبک آمریکایی باز کند و به سرعت خود را با این طرز عمل جدید وفق داد. تسکو در دهه ۱۹۹۰ به سرعت رشد کرد که بخشی از آن بواسطه ادغامها و تملکها بود. در سال ۱۹۹۵ پیشتاز بازار بریتانیا شد و امروزه بیش از نیم میلیون نفر را در اروپا و آسیا در استخدام خود دارد.
تسکو راهبرد قیمت گذاری خود را از همان روزهای اول با شعار «ارزان بفروش» شکل داده بود. هدفش این است که به همه بخشهای بازار سرک بکشد، و در کنار محصولات رده استاندارد خود، برخی را با برچسب ممتاز و برخی دیگر را با برچسب خوب عرضه کند. برنامه پول (Money Programme) تلویزیون بی بی سی سه اصل تسکو را چنین خلاصه میکند: «همه جا باش»، «همه چیز بفروش» و «به همه بفروش».
شعار جک کوهن این بود که «روی هم انبار کن و ارزان بفروش». او کارش را بعنوان یک دلال خیابانی در محلههای شرقی لندن در سال ۱۹۱۹ آغاز و اولین فروشگاهش را ۱۲ سال بعد افتتاح کرد. امروزه ۱ پوند از هر ۷ پوندی که در بریتانیا در یک مغازه خرج میشود در یک مغازه تِسکو خرج میشود و کمپانی در دهه ۱۹۹۰ توسعه جهانی پیدا کرد؛ در سال ۲۰۱۴ تسکو از همه خرده فروشان جهان بهجز والمارت سود بیشتری داشته است. همانطور که کوهن پیشنهاد کرده بود، پایین نگه داشتن قیمتها یکی از راهبردهای ممکن برای بنگاه اقتصادیی است که میخواهد سودش را به حداکثر برساند: با اینکه سود حاصل از هر قلم سود کمی است، اما قیمت پایین میتواند آنقدر مشتریان زیادی را جلب کند که سود نهایی بسیار زیاد باشد.
بنگاههای اقتصادی دیگر راهبردهای کاملاً متفاوتی در پیش میگیرند. اپل قیمتهای بالایی برای آیفون و آیپدهایش اعلام میکند و سودش را با تعیین یک قیمت اضافی تأمین بالا میبرد و نه با پایین آوردن قیمتها برای جلب مشتریان بیشتر. برای مثال، از فاصله آوریل ۲۰۱۰ تا مارس ۲۰۱۲ سود هر قلم یا واحد در مورد ایفون اپل بین ۴۹ تا ۵۸ درصد قیمت بوده است. درطی همین دوره، سود عملی تِسکو در هر قلم بین ۶ تا ۶.۵ درصد بود.
اما سود یک بنگاه اقتصادی به مسائلی بیش از تعیین قیمت صحیح بستگی دارد. انتخاب محصول و توانایی جلب مشتری، تولید با هزینه کمتر و کیفیت بیشتر نسبت به رقبا همه و همه اهمیت دارند. همچنین باید بتوانند کارکنانی استخدام کرده و حفظ کنند که بتوانند زمینه تحقق همه این مسائل را فراهم کنند.
شکل ۷.۲ تصمیمات کلیدیای که یک بنگاه اقتصادی میگیرد را نشان میدهد. در این فصل ما بطور خاص تمرکز خود را بر نحوه انتخاب قیمت محصول و کیفیت تولید از سوی بنگاه اقتصادی خواهیم گذاشت. این مسأله به تقاضایی که بنگاه اقتصادی باآن روبرو است – یعنی تمایل مشتریان بالقوه به خرید محصولات آن – و همچنین هزینه تولید آن بستگی خواهد داشت.
تقاضا برای یک محصول، به قیمت آن بستگی دارد، و هزینههای تولید میتواند به تعداد اقلام تولیدی بستگی داشته باشد. اما یک بنگاه اقتصادی میتواند بهشکل فعالانه بر تقاضای محصول و بر هزینهها، به اشکالی غیر از قیمت و کمیت هم تأثیر بگذارد. همانطور که در فصل ۲ دیدیم، نوآوری و خلاقیت میتواند به محصولات جدید و جذاب، و یا به هزینه تولید پایینتر منجر شود. اگر بنگاه اقتصادی بتواند بهشکل موفقیت آمیزی نوآوری کند میتواند از بهره برخوردار شود – دست کم برای مدتی کوتاه تا زمانی که دیگران خود را به او برسانند. اگر بخواهد که باز هم پیشتاز بماند احتمالاً به نوآوری بازهم بیشتری نیاز خواهد داشت. تبلیغات میتواند تقاضا را افزایش دهد. و همانطور که در فصل ۶ دیدیم، بنگاه اقتصادی تعیین دستمزد را که یکی از بخشهای مهم هزینههایش را تشکیل میدهد، در اختیار دارد. و در فصلهای بعدی خواهیم دید که بنگاه اقتصادی برای تحت الشعاع قرار دادن مالیاتها و قوانین زیست محیطی هم در جهت کاستن از هزینههای تولید خود، هزینه میکند.
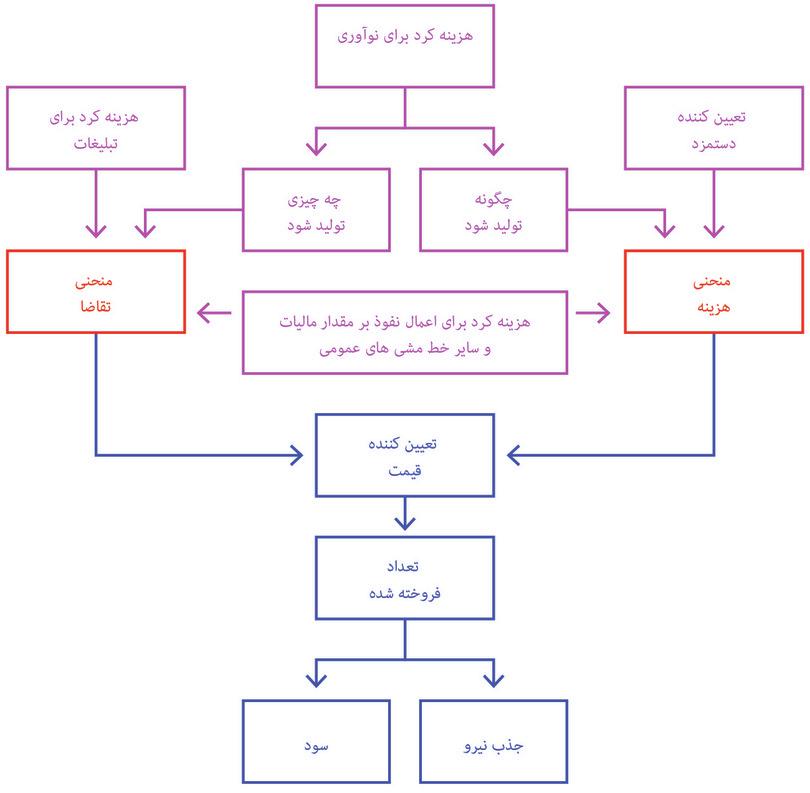
تصمیمات بنگاه اقتصادی
شکل ۷.۲ تصمیمات بنگاه اقتصادی
۷.۱ غلات صبحانه: انتخاب قیمت
- منحنی تقاضا
- منحنی تقاضا به ما میگوید که مصرفکنندگان در هر قیمتِ ممکن، چه تعداد خرید خواهند داشت.
بنگاه اقتصادی برای تصمیم درباره قیمت اعلامی به اطلاعاتی در مورد تقاضا نیاز دارد: اینکه مشتریان بالقوه تمایل دارند. شکل ۷.۳ منحنی تقاضای شرکت اپل-سینامون چیروز، یک صبحانه غلات آماده که در سال ۱۹۸۹ توسط شرکت جنرال میلز معرفی شد را نشان میدهد. جری هاسمن اقتصاددان در سال ۱۹۹۶ تلاش کرد تا براساس دادههای مربوط به فروش هفتگی غلات صبحانه خانوادهها در شهرهای آمریکا، تخمین بزند که مقدار هفتگی غلهای که مشتریان در یک شهر نوعی تمایل به خرید آن دارند، چگونه برحسب قیمت آن در هر پوند (هر کیلوگرم ۲.۲ پوند است) تغییر میکند. برای مثال از روی شکل ۷.۳ میتوانید ببینید که اگر قیمتها ۳ دلار باشند، تقاضای مشتریان برای چیروز ۲۵۰۰۰ پوند خواهد بود. در مورد اغلب محصولات، هرچه قیمت پایینتر باشد، تمایل مشتریان به خرید بیشتر است.
چگونه اقتصاددانان از دادهها میآموزند برآورد منحنی تقاضا با استفاده از پیمایش
جری هاسمن برای برآورد منحنی تقاضای اپل-سینامون چیروز از دادههای خرید استفاده کرد. روش دیگر که خصوصاً برای بنگاههای اقتصادیی که محصولات جدید عرضه میکنند مناسب است، استفاده از پیمایش مشتریان است. فرض کنید که در مورد تقاضای بالقوه برای گردشگری فضایی تحقیق میکنید. میتوانستید از مشتریان بالقوه بپرسید:
«برای یک پرواز ۱۰ دقیقهای به فضا چقدر حاضرید پرداخت کنید؟»
اما ممکن است تصمیمگیری برای آنها سخت باشد، یا بدتر، ممکن است اگر فکر کنند که پاسخشان برای قیمتی که نهایتاً اعلام خواهد شد تأثیر میگذارد، دروغ بگویند. راه بهتر برای پیداکردن تمایل حقیقی آنها به پرداخت این است که بپرسیم:
«آیا تمایل دارید که ۱۰۰۰ دلار برای یک پرواز ۱۰ دقیقهای به فضا پرداخت کنید؟»
در سال ۲۰۱۱ یک نفر این کار را انجام داده است و بنابراین ما امروز تقاضای مصرفی برای پرواز فضایی را میدانیم:2
چه محصول مورد نظر غله صبحانه باشد و چه سفر به فضا، روش یکسان است: اگر قیمتهای مورد نظر را جابجا کنید و نظر تعداد زیادی از مشتریان را جویا شوید خواهید توانست برآوردی از اینکه چه سهمی از مردم تمایل پرداخت هر یک از قیمتها دارند بدست بیاورید. بهاین ترتیب خواهید توانست منحنی کل تقاضا را برآورد کنید:
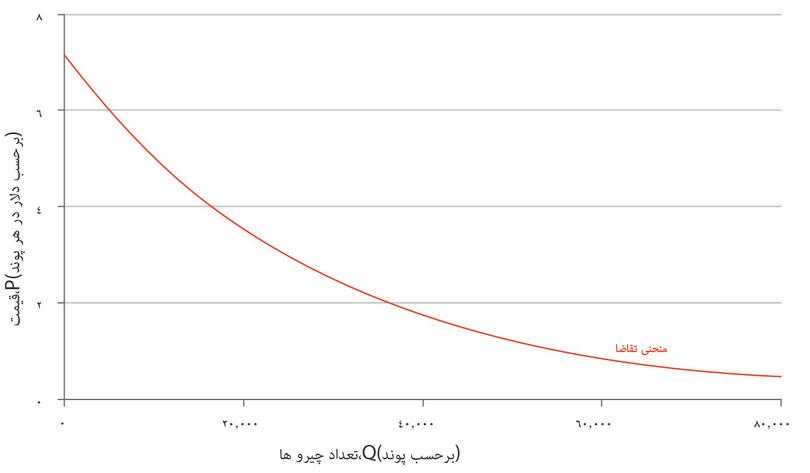
تقاضای برآورد شده برای اپل-سینامون چیروز
شکل ۷.۳ تقاضای برآورد شده برای اپل-سینامون چیروز
Adapted from Figure 5.2 in Jerry A. Hausman. 1996. ‘Valuation of New Goods under Perfect and Imperfect Competition’. In The Economics of New Goods, pp. 207–248. Chicago, IL: University of Chicago Press.
اگر شما مدیری در شرکت جنرال میلز بودید، قیمت اپل-سینامون چیروز را در این شهر چقدر تعیین میکردید و چند پوند غله تولید میکردید؟
لازم است توجه داشته باشید که این تصمیم چگونه بر سود شما (یعنی بر تفاوت میان درآمدهای حاصل از فروش و هزینههای تولید) تأثیر خواهد گذاشت. فرض کنید که هزینه هر قلم (هزینه تولید هر پوند) از اپل-سینامون چیروز ۲ دلار است. برای اینکه سود حداکثری داشته باشید، باید بتوانید دقیقاً همان مقداری تولید کنید که انتظار فروشش را دارید، و نه بیشتر. در این صورت، درآمد، هزینهها، و سود عبارت خواهند بود از:
بنابراین ما یک فرمول سود داریم:
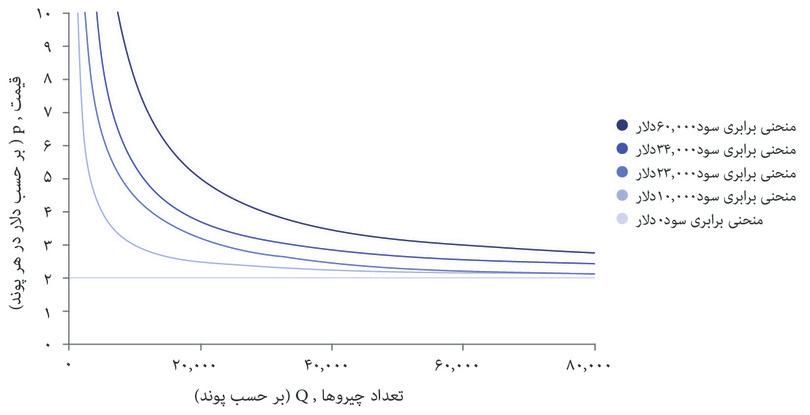
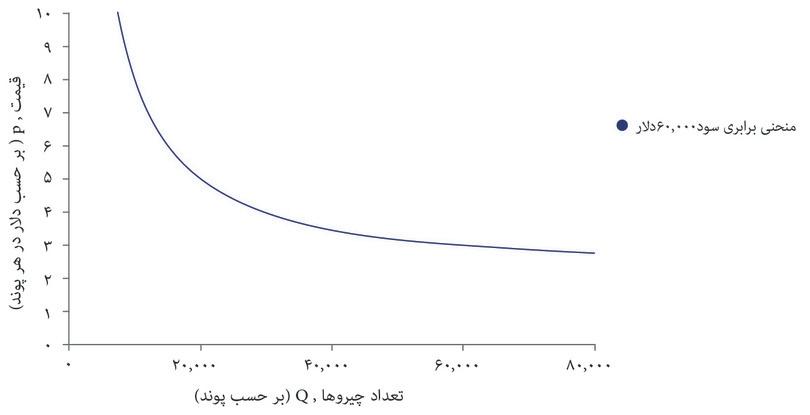
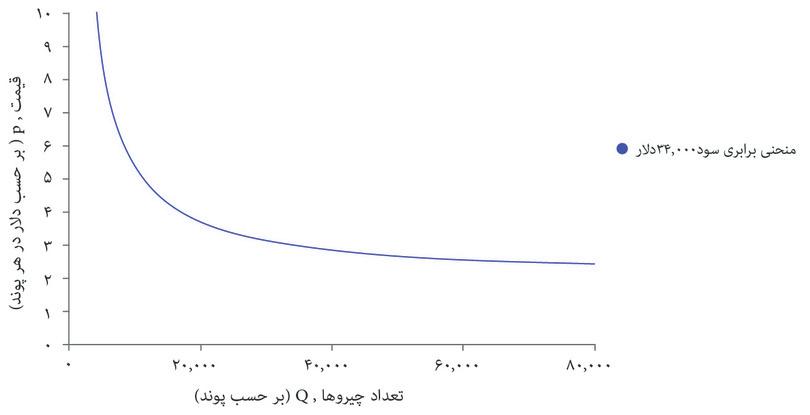
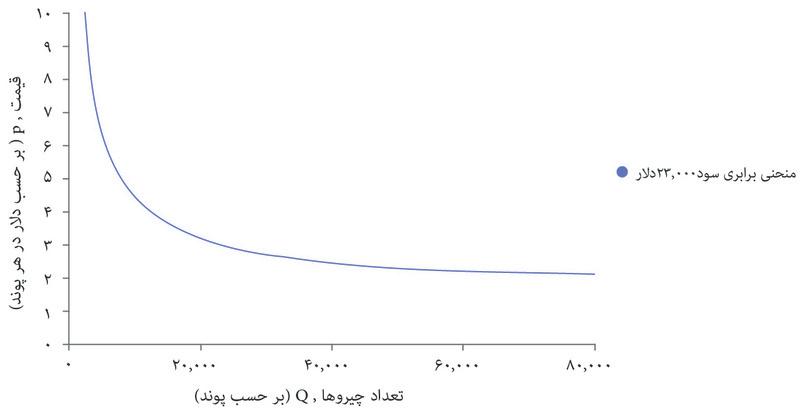
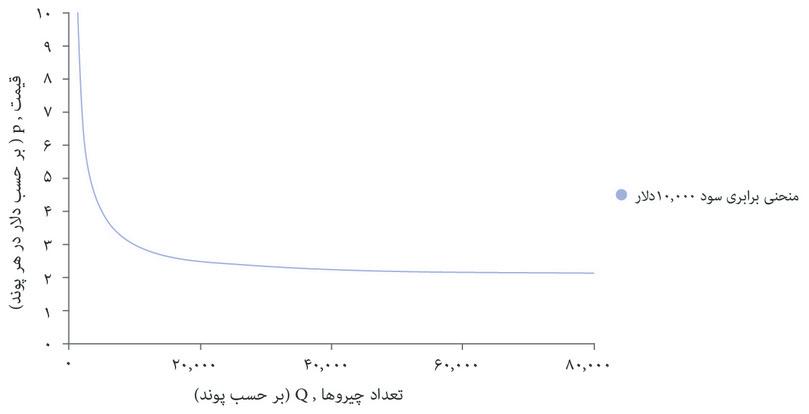
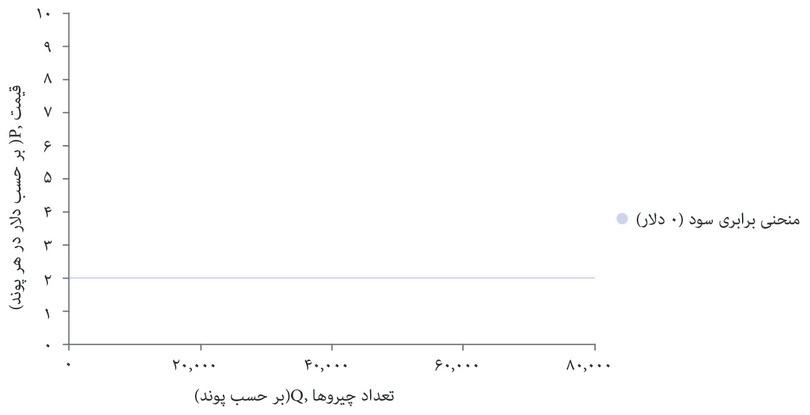
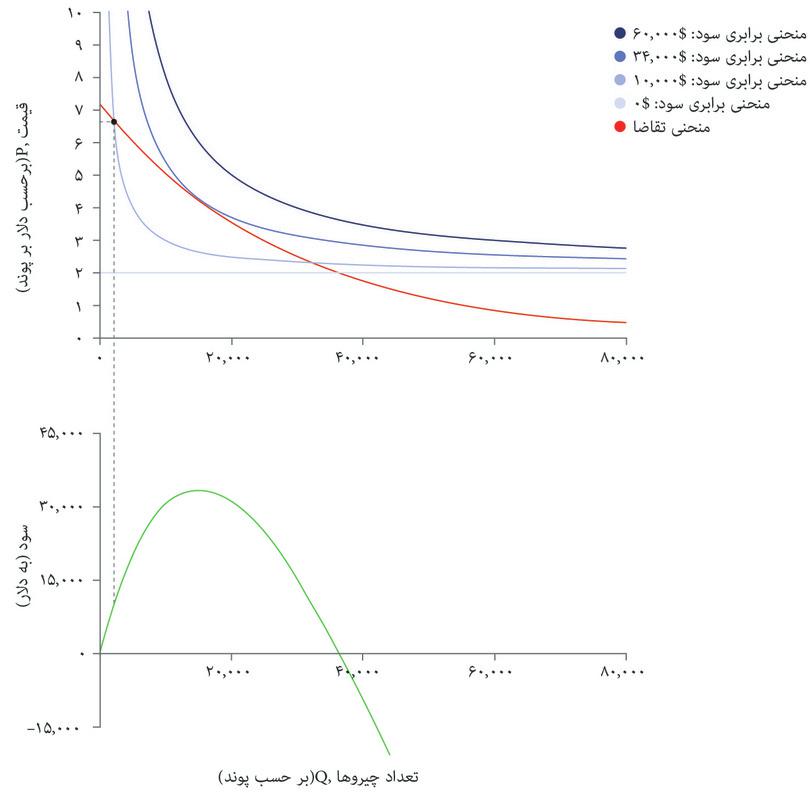
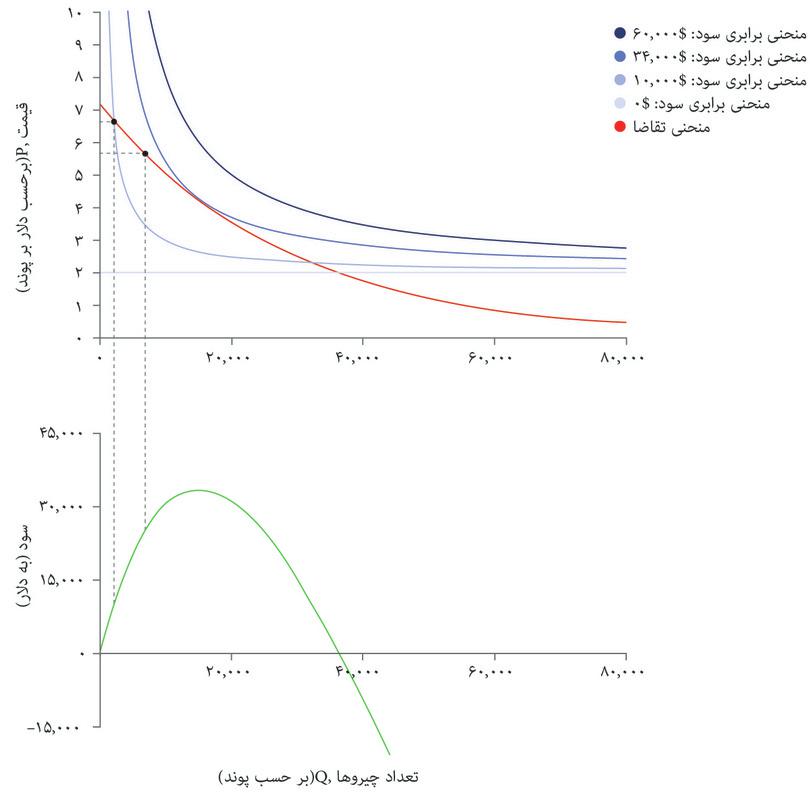
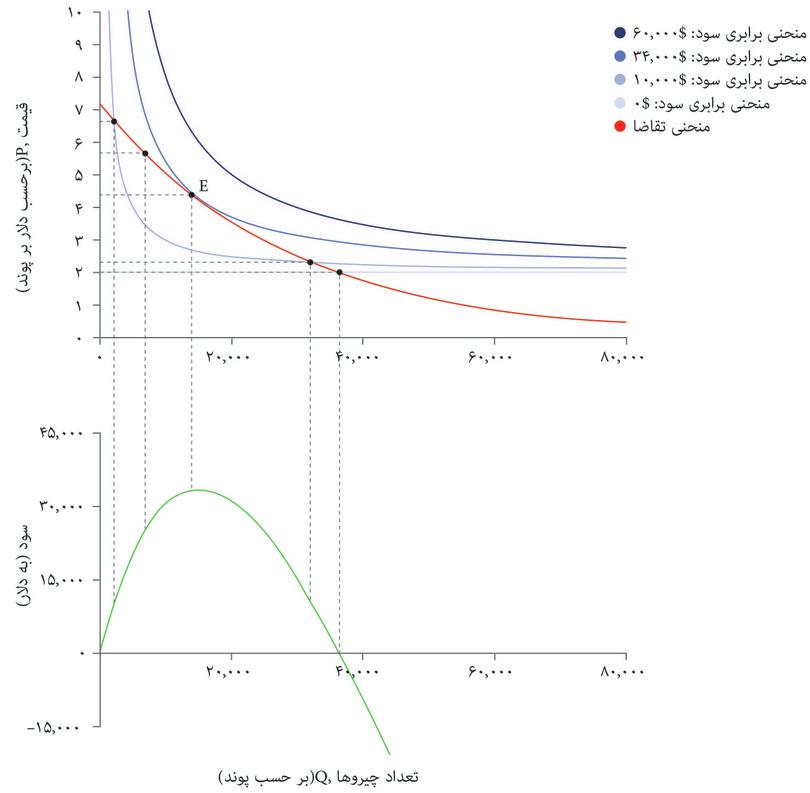
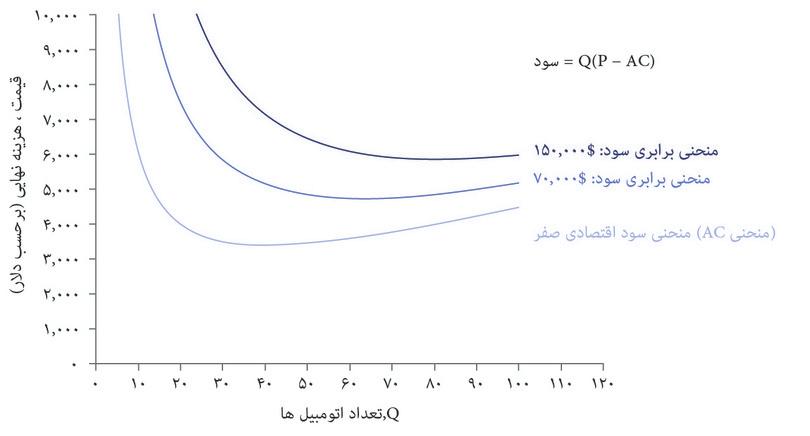
با استفاده از این فرمول میتوانید سود حاصل از هر انتخاب قیمت و تعداد را محاسبه کنید و منحنیهای برابری سود را مثل شکل ۷.۴ ترسیم کنید. درست همانطور که منحنیهای بیتفاوتی نقاطی در نمودار را قطع میکنند که سطح مطلوبیتِ یکسانی را نشان میدهند، منحنیهای برابری سود هم نقاطی را قطع میکنند که سطح سود یکسانی را نشان میدهند. منحنیهای برابری سود را میتوان همان منحنیهای بیتفاوتی بنگاه اقتصادی محسوب کرد: ترکیبات مختلفی از قیمت و تعداد که درنهایت سود یکسانی میدهند برای بنگاه اقتصادی تفاوتی با هم ندارند.
پرسش ۷.۱ (همه پاسخ های صحیح را انتخاب کنید)
هزینه تولید یک شرکت ۱۲پوند در هر قلم خروجی است. اگر P قیمت کالای خروجی و Q تعداد اقلام تولیدشده باشد، کدامیک از گزینه های زیر صحیح است؟
- (الف) در نقطه (Q، P) = (۲۰۰۰، ۲۰), سود = (۲۰ – ۱۲) × ۲۰۰۰ = £۱۶۰۰۰.
- (ب) در نقطه (Q، P) = (۱۲۰۰، ۲۴), سود= (۲۴ – ۱۲) × ۱۲۰۰۰ = £۱۴۴۰۰. در نقطه(Q، P) = (۲۰۰۰، ۲۰)، سود = (۲۰ – ۱۲) × ۲۰۰۰ = £۱۶,۰۰۰است. بنابراین نقطه (۲۰۰۰، ۲۰) روی منحنی برابری سود بالاتری قرار دارد.
- (ج) در نقطه (Q، P) = (۲۰۰۰، ۲۰), سود = (۲۰ – ۱۲) × ۲۰۰۰ = £۱۶۰۰۰است. در نقطه (Q, P) = (۴۰۰۰، ۱۶)، سود = (۱۶ – ۱۲) × ۴۰۰۰ = £۱۶۰۰۰است. بنابراین، این دو نقطه روی منحنی برابری سود واحدی قرار دارند.
- (د) در قیمت ۱۲ دلار، شرکت سودی نمی کند. بنابراین نقطه (۵۰۰۰، ۱۲) روی منحنی برابری سودِ افقی ای قرار دارد که سودِ صفر را نشان می دهد.
پرسش ۷.۲ (همه پاسخ های صحیح را انتخاب کنید).
شرکتی را در نظر بگیرید که قیمت واحدِ آن (هزینه تولید یک قلم یا واحد از خروجی) در همه سطوحِ خروجی یکسان باشد. کدامیک از گزاره های زیر صحیح است؟
- (الف) منحنی برابری هزینه همه ترکیباتی از قیمت و تعداد را به هم وصل می کند که سود یکسانی برای شرکت دارند.
- (ب) اگر سود بالا باشد، قیمت باید بالاتر از هزینه هر واحد باشد. پس اگر خروجی افزایش پیدا کرده باشد، قیمت را باید آنقدر کم کرد که سطح سود را ثابت نگه داشت. بنابراین منحنی برابری سود باید شیب رو به پائین داشته باشد.
- (ج) می توانید به ازای هر ترکیبی از قیمت و تعداد، سود را محاسبه کنید و سپس سایر نقاطی را که سود یکسانی دارند پیدا کنید و خط برابری سود را ترسیم کنید.
- (د) اگر قیمت از هزینه هر واحد بالاتر باشد، آنوقت در صورت افزایش خروجی، قیمت را باید جهت ثابت نگه داشتنِ سود پائین آورد و بنابراین خط برابری هزینه شیب روبه پائین خواهد داشت.
ممکن است برای بدست آوردن یک سود بالا بخواهید که هم قیمت و هم تعداد را تا حد ممکن بالا نگه دارید، اما منحنی تقاضا شما را محدود میکند: اگر قیمت بالا را انتخاب کنید، تنها خواهید توانست تعداد کمی بفروشید؛ و اگر بخواهید که تعداد زیادی بفروشید، باید قیمت پایینتری انتخاب کنید.
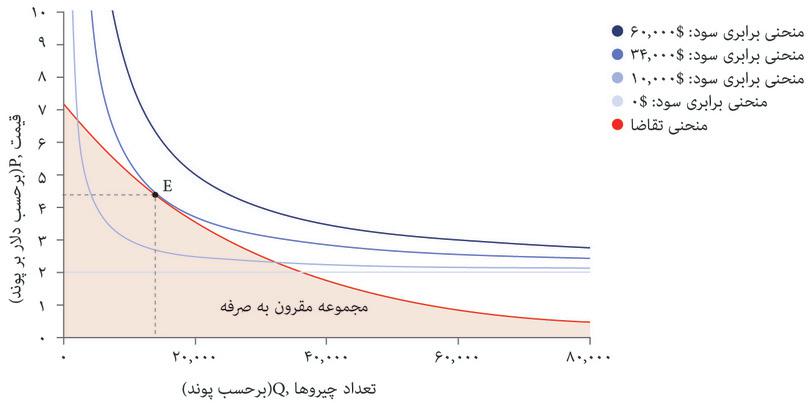
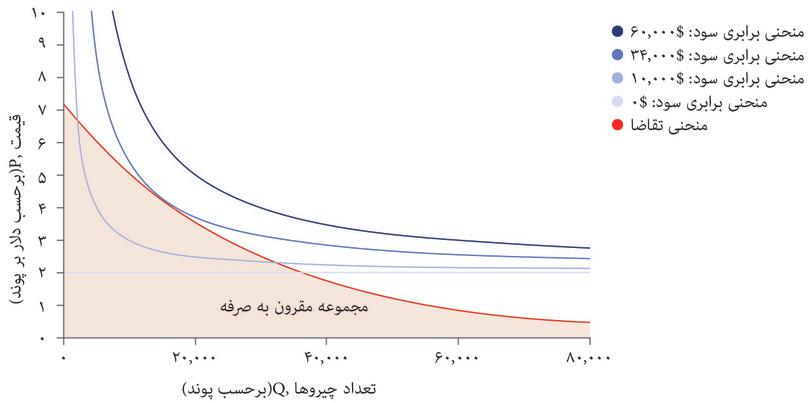
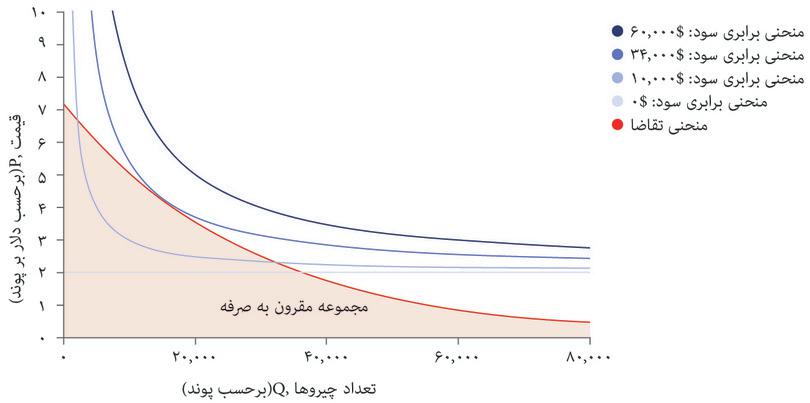
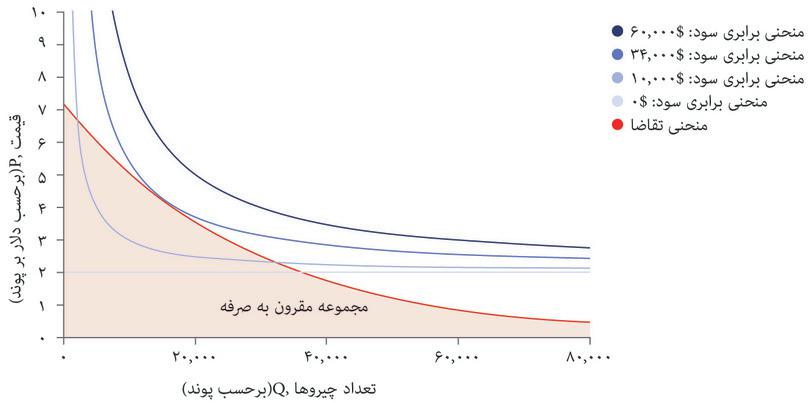
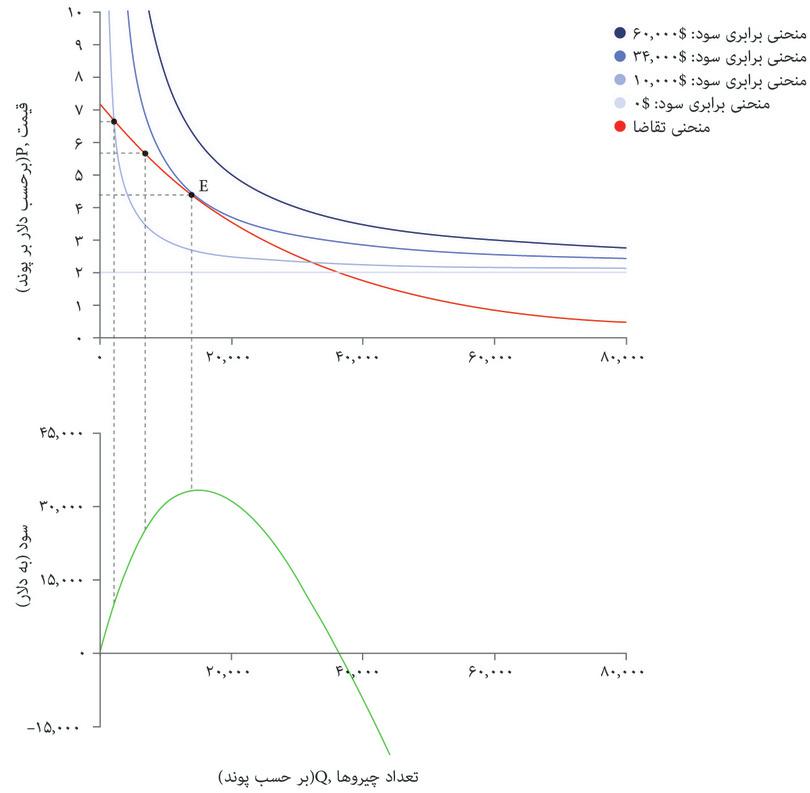
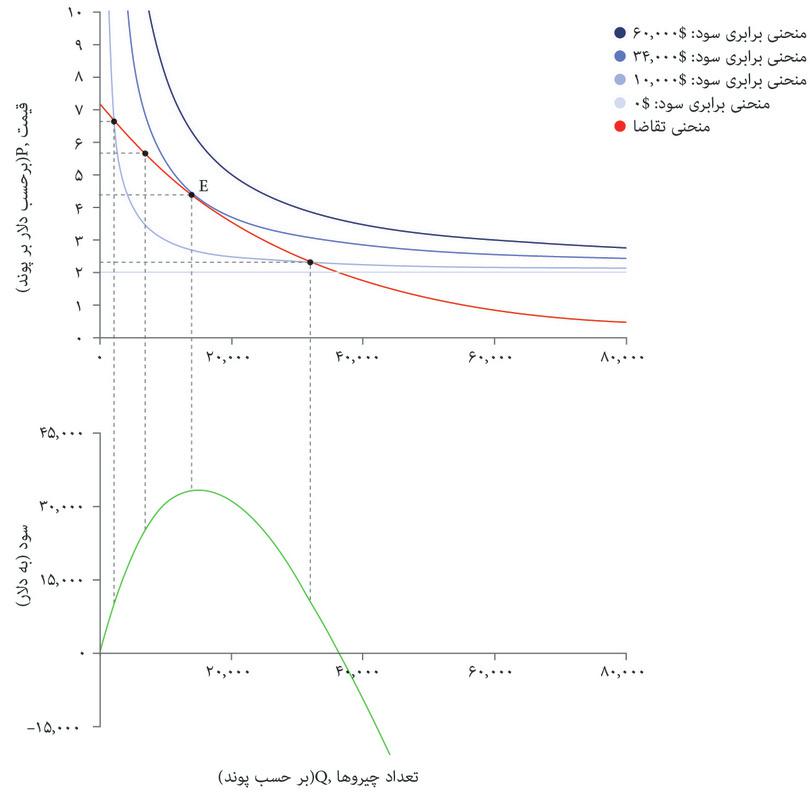
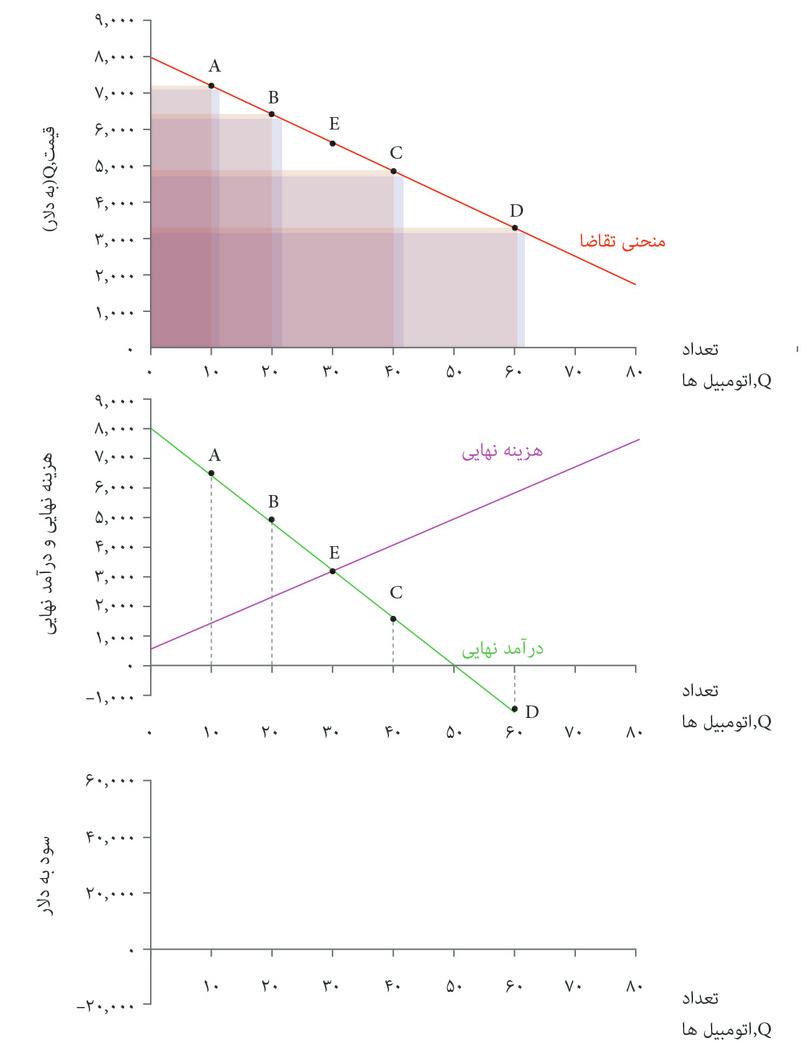
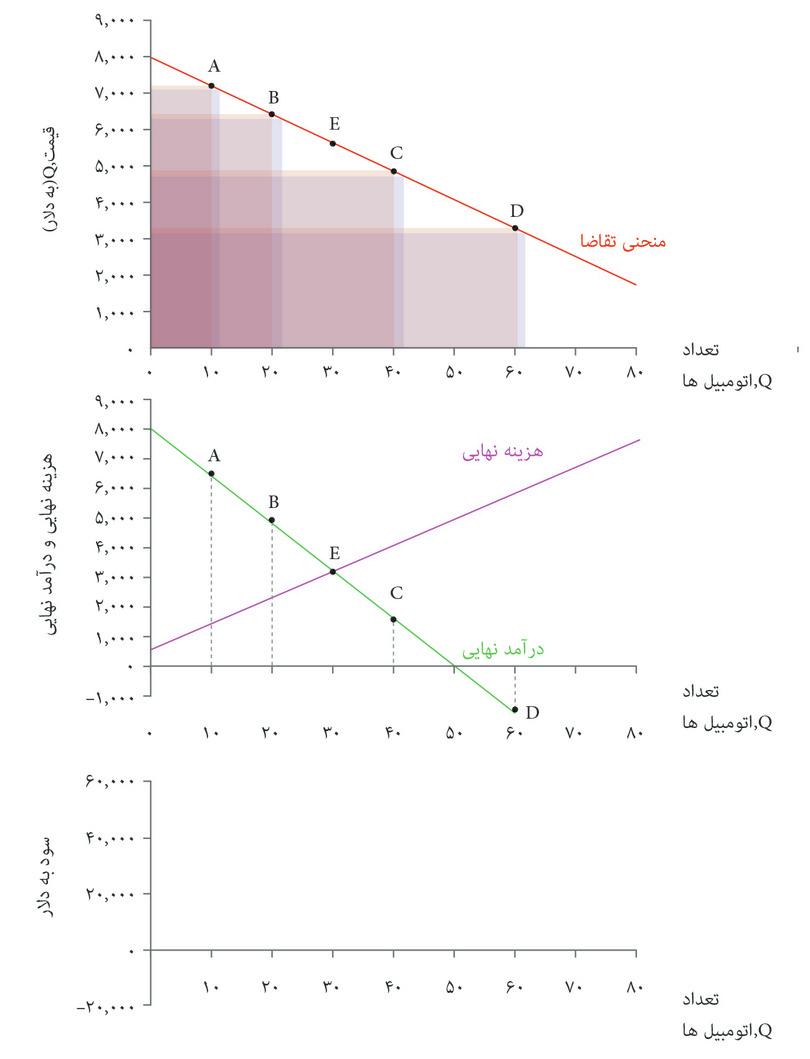
منحنی تقاضا است که تعیین میکند چه چیزی مقرون بهصرفه است. شکل ۵.۷ الف منحنیهای برابری سود و منحنیهای تقاضا را با هم نشان میدهد. شما با مشکلی مشابه مشکل الکسی در فصل ۳ روبهرو هستید؛ دانشجویی که میخواست نقطهای در مجموعه مقرون بهصرفهگی خود را انتخاب کند که در آن مطلوبیت او به حداکثر برسد. شما هم میخواهید ترکیب مقروت بهصرفهای از قیمت و تعداد را انتخاب کنید که سود شما را به حداکثر برساند.
بهترین راهبرد شما این است که نقطه E در شکل ۷.۵ الف را انتخاب کنید: یعنی ۱۴۰۰۰ پوند غله تولید کنید، و با قیمت ۴.۴ دلار در هر پوند بفروشید و ۳۴۰۰۰ دلار سود بدست بیاورید. درست همانطور که در مورد الکسی در فصل ۳ دیدیم، ترکیب بهینه از قیمت و تعداد، مستلزم موازنه دو بده-بستان است. ما فرض کردیم که بعنوان مدیر تنها سود برای شما مهم است و نه هیچ ترکیب خاصی از قیمت و تعداد.
- نرخ نهایی جانشینی (MRS)
- بده-بستانی که فرد مایل است بین دو کالا انجام دهد. در هر نقطه، این عبارت است از شیبِ منحنی بیتفاوتی. همچنین نگاه کنید به نرخ نهایی تبدیل.
- نرخ نهایی تبدیل(MRT)
- تعداد کالایی که باید برای دستیابی به یک واحد اضافی از کالایی دیگر قربانی شود. در هر نقطه، این عبارت است از شیبِ مرزِ مقرونبهصرفگی. همچنین نگاه کنید به نرخ نهایی جانشینی.
- منحنی برابری سود، منحنی بیتفاوتی شما است، و شیب آن در هر نقطه نمایانگر بده-بستانی است که مایلید میان قیمت و تعداد برقرار کنید – یعنی نرخ نهایی جانشینی MRSشما. یعنی مایل خواهید بود که اگر سود یکسان باشد، قیمت بالاتری را جایگزین تعداد کم کنید.
- شیب منحنی تقاضا، بده-بستانی است که شما ملزم و محدود به انتخاب آن هستید – یعنی نرخ نهایی تبدیل MRTشما، یا نرخی که منحنی تقاضا به شما اجازه میدهد تعداد را به قیمت «تبدیل» کنید. نمیتوانید بدون پایین آوردن تعداد، قیمت را بالا ببرید، زیرا مشتریان کمی هستند که حاضر باشند محصول گرانتری خریداری کنند.
این دو بده-بستان، در انتخابی از قیمت و تعداد که سود را به حداکثر میرساند، موازنه میشوند.
مدیر جنرال میلز احتمالاً در مورد این تصمیم به این شکل فکر نمیکرد.
شاید قیمت بیشتر براساس آزمون و خطا انتخاب شده و از تجارب گذشته و پیماپیشهای بازاریابی هم استفاده کرده است. اما انتظار میرود که به هر حال بنگاه اقتصادی راه خود در دستیابی به قیمت و تعدادی که حداکثر سود را داشته باشد بهنحوی پیدا کند. هدف تحلیل اقتصادی ما نه الگوسازی از فرآیند اندیشیدن مدیر، که فهمِ نتیجه، و رابطه آن با هزینه بنگاه اقتصادی و تقاضای مصرف کننده است.
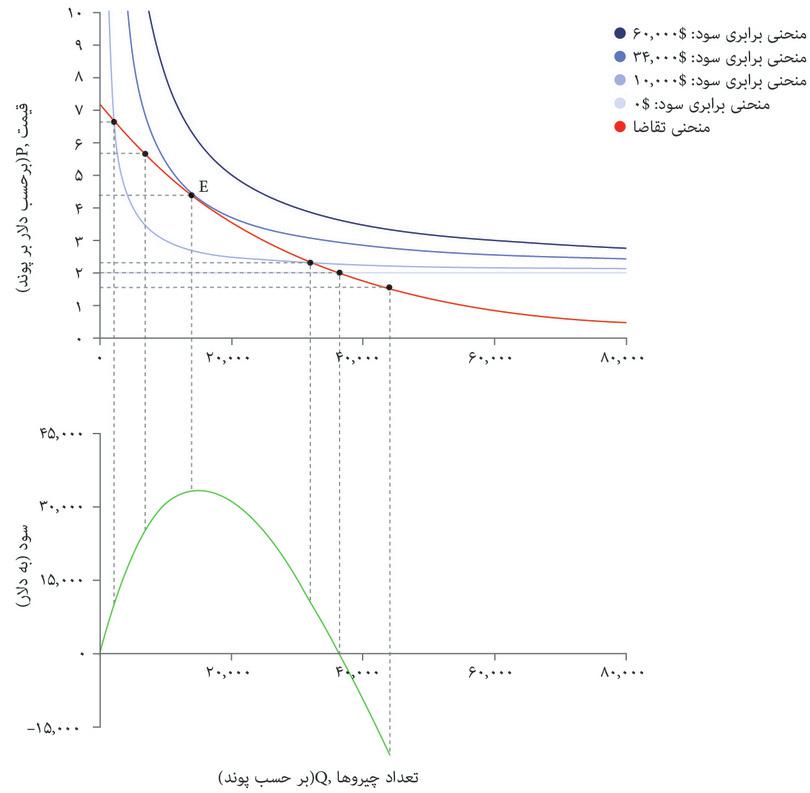
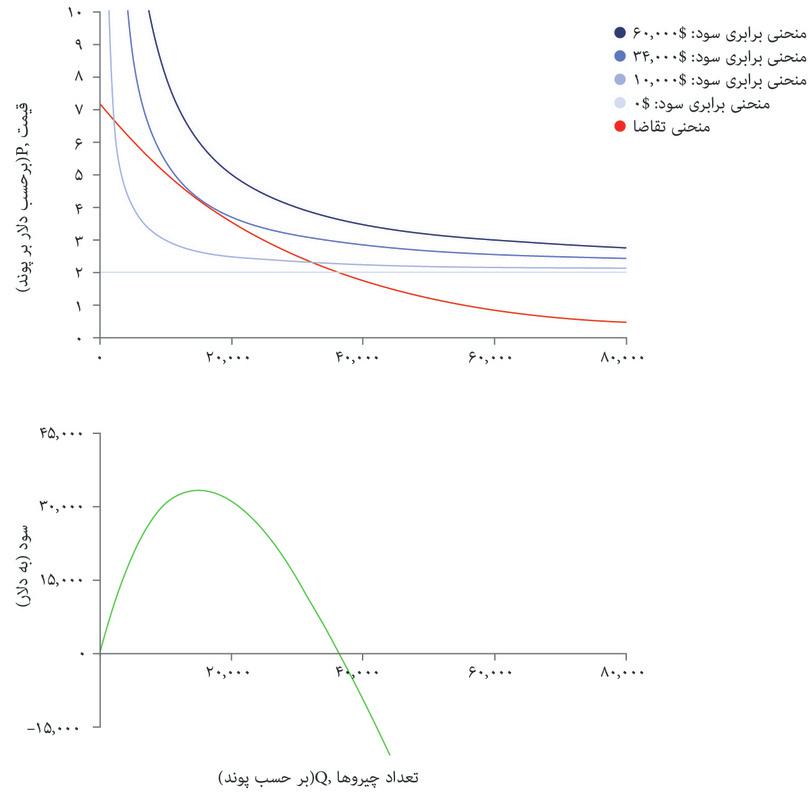
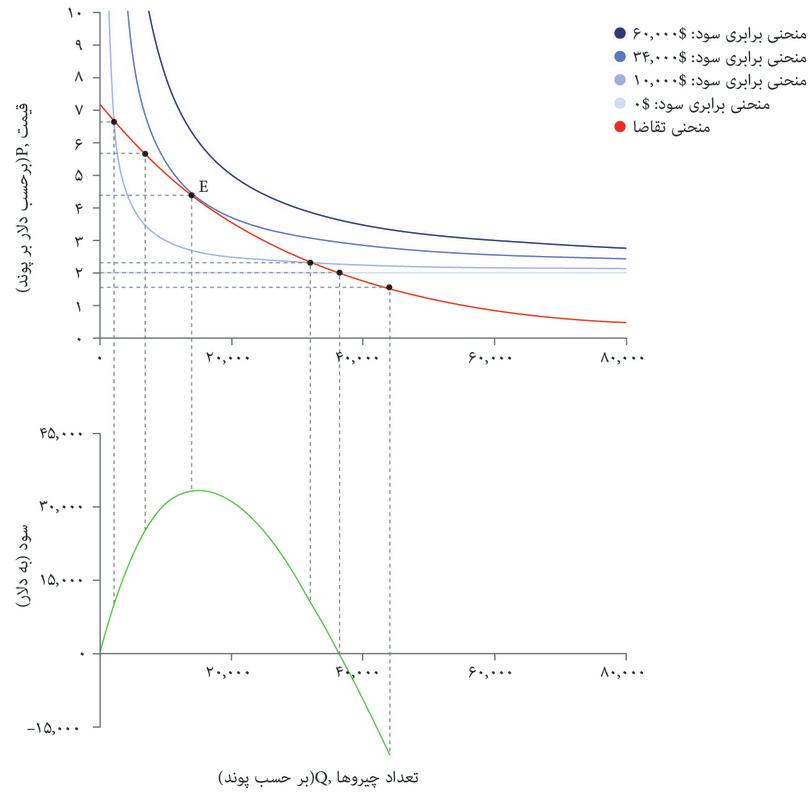
حتی از نقطه نظر یک اقتصاددان هم، راههای دیگری برای اندیشیدن به حداکثرسازی سود وجود دارد. قسمت پایینی شکل ۷.۵ ب نشان میدهد که در هر نقطه روی منحنی تقاضا چقدر سود ایجاد خواهد شد.
نموداری که در پایین قاب قرار دارد تابع سود است: نشان میدهد که اگر تصمیم بگیرید تعدادی تولید کنید، و بالاترین قیمتی را که برحسب تابع تقاضا به شما اجازه فروش آن تعداد را میدهد انتخاب کنید، چه مقدار سود خواهید داشت. و به ما نشان میدهد که شما سود حداکثری ۳۴۰۰۰ دلار را با تولید ۱۴۰۰۰ پوند غله بدست خواهید آورد.
پرسش ۷.۳ (یک پاسخ را انتخاب کنید).
جدول زیر تقاضای بازار Q تعداد از کالایی با قیمت های مختلف Pرا نشان می دهد.
| Q | ۱۰۰ | ۲۰۰ | ۳۰۰ | ۴۰۰ | ۵۰۰ | ۶۰۰ | ۷۰۰ | ۸۰۰ | ۹۰۰ | ۱۰۰۰ |
| P | £۲۷۰ | £۲۴۰ | £۲۱۰ | £۱۸۰ | £۱۵۰ | £۱۲۰ | £۹۰ | £۶۰ | £۳۰ | £۰ |
هزینه تولید هر واحد برای شرکت ۶۰ پوند است. براساس این اطلاعات، کدامیک از گزاره های زیر صحیح است؟
- (الف) اگر Q = ۱۰۰ باشد، سود = (۲۷۰ – ۶۰) × ۱۰۰ = £۲۱۰۰۰است.
- (ب) اگر Q = ۴۰۰ سود = (۱۸۰ – ۶۰) × ۴۰۰ = £۴۸۰۰۰است. اگر سود را برای هر نقطه روی منحنی تقاضا محاسبه کنید، خواهید دید که سود در نقاط دیگر پائین تر است.
- (ج) حداکثر سود وقتی بدست می آید که Q = ۴۰۰، باشد، یعنی نقطه ای که سود = (۱۸۰ – ۶۰) × ۴۰۰ = £۴۸۰۰۰.
- (د) در همه خروجی های بالای ۸۰۰، شرکت ضرر خواهد داد (یعنی سود منفی خواهد داشت). روی خود نقط ۸۰۰، سود برابر با صفر است.
تمرین ۷.۱ تغییرات در بازار
نمودارهایی رسم کنید که نشان دهد منحنیهای شکل ۷.۵الف در هر کدام از موارد زیر چه تغییراتی خواهد داشت:
- یک کمپانی رقیب که برند مشابهی را تولید میکند، قیمتها را میشکند.
- هزینه تولید اپل-سینامون چیروز به ۳ دلار برای هر پوند افزایش پیدا میکند.
- شرکت جنرال میلز کارزاری تبلیغاتی براه میاندازد که ۱۰۰۰۰ دلار در هفته هزینه دارد.
می توانید بگویید که در هر کدام از این موارد چه اتفاقی برای قیمت و سود میافتد؟
۷.۲ صرفه جویی-ناشی-از مقیاس و مزایای هزینهای تولید کلان مقیاس
چرا شرکتهایی مثل والمارت و اینتل و فداِکس تا این حد بزرگ شده اند؟ یک دلیل مهمِ اینکه چرا یک بنگاه اقتصادی بزرگ ممکن است سودآورتر از یک بنگاه اقتصادی کوچک باشد، این است که بنگاه اقتصادی بزرگ خروجی خود را با هزینه-در-واحد کمتری تولید میکند. به دو دلیل این احتمال وجود دارد:
-
مزایای ناشی از فناوری: تولید کلان-مقیاس اغلب ورودی کمتری بهازای هر واحد خروجی استفاده میکند.
-
مزایای ناشی از هزینه: در بنگاههای اقتصادی بزرگتر هزینههای ثابتی چون تبلیغات تأثیر کمتری بر هزینه هر واحد دارند. و ممکن است بدلیل قدرت چانهزنیای که دارند بتوانند ورودیهای خود را با قیمت کمتری بخرند.
- صرفهجویی ناشی از مقیاس
- صرفهجوییهای ناشی از مقیاس زمانی رخ میدهند که دوبرابرکردن کل ورودیهای یک فرآیند تولیدی، باعث افزایش خروجی به میزانی بیش از دو برابر میشود. شکل منحنی میانگین هزینه درازمدتِ یک شرکت، هم تابعِ بازگشت به مقیاس در تولید است و هم تابع تاثیرِ مقیاس بر قیمتهایی که برای ورودیهای خود میپردازد.. همچنین تحت عنوان روندِ کاهشیِ بازگشت به مقیاس هم شناخته میشود. و همچنین نگاه کنید به: صرفهجویی ناشی از مقیاس.
اقتصاددانان از برای توصیف مزایای فناورانه تولید کلان-مقیاس، از اصطلاحِ صرفه جویی ناشی از مقیاس یا بازگشتهای تصاعدی استفاده میکنند. برای مثال اگر دوبرابر کردن مقدار هر ورودیای که بنگاه اقتصادی استفاده میکند، سود بنگاه اقتصادی را سه برابر میکند، آنگاه بنگاه اقتصادی با بازگشتهای تصاعدی روبهرو است.
- عدمصرفهجویی ناشی از مقیاس
- این حالت وقتی اتفاق میافتد که دوبرابرکردنِ کلیه ورودیها به یک فرآیند تولید، خروجی را به میزانی بیش از دوبرابر افزایش دهد. شکلِ منحنی میانگینِ هزینهی یک شرکت در درازمدت هم به میزانِ بازگشت به مقیاس در تولید بستگی دارد و هم به اثرِ مقیاس بر قیمتهایی که برای ورودیهای خود میپردازد. همچنین تحت عنوانِ روندِ افزایشیِ بازگشت به مقیاس هم شناخته میشود. همچین به عنوان کاهش بازده به مقیاس شناخته میشود. همچنین نگاه کنید به: صرفهجویی ناشی از مقیاس.
- روندِ ثابتِ بازگشت به مقیاس
- این حالت وقتی اتفاق میافتد که دوبرابرکردنِ همه ورودیها به فرایند تولید، خروجی را دوبرابر میکند. شکلِ منحنی میانگین هزینه درازمدتِ یک شرکت هم به بازگشت به مقیاس در تولید و هم به اثرِ مقیاس بر قیمتهایی که برای ورودیهای خود میپردازد بستگی دارد. همچنین نگاه کنید به: روندِ افزایشیِ بازگشت به مقیاس، و روندِ کاهشی بازگشتِ به مقیاس.
صرفه جوییها و اتلافهای ناشی از مقیاس
اگر همه ورودیها را به یک نسبت تغییر دهیم، و اینکار:
*خروجی را بیش از آن نسبت افزایش دهد، آنگاه میگوییم که فناوری، بازگشتهای تصاعدی برای مقیاس تولید یا صرفه جویی ناشی از مقیاس به همراه دارد.
- خروجی را کمتر از آن نسبت افرایش دهد، آنگاه میگوییم فناوری، بازگشتهای تنازلی برای مقیاس تولید یا اتلاف ناشی از مقیاسبه همراه دارد.
- خروجی را به همان نسبت افزایش دهد، آنگاه میگوییم که فناوری، بازگشتهای ثابت برای مقیاس تولید بهدنبال دارد.
صرفه جویی ناشی از مقیاس میتواند نتیجه تخصصی شدن مناسبات درون بنگاه اقتصادی باشد، که اجازه میدهد کارکنان بهترین کاری را که از عهدهاش بر میآیند انجام دهند و با محدودکردن دایره مهارتی موردنیاز برای هر کارگر زمان آموزش را کاهش میدهد. صرفه جویی ناشی از مقیاس همچنین میتواند از دلایل صرفاً مهندسی ناشی شود: مثلاً انتقال حجم بیشتری از یک مایع مستلزم لولههای بزرگتری است، اما دو برابر شدن ظرفیت لوله، قطر لوله (و مواد لازم برای ساخت آن) را به مقداری کمتر از مضرب دو افزایش میدهد. برای اثبات این قضیه به بخش اندازه و هزینه لوله در قسمت انیشتین رجوع کنید.
اما عدم صرفه جویی (یا اتلاف) ناشی از مقیاسهم وجود دارد. مالکان، مدیران، ناظران کار و کارگران خط تولید را در نظر آورید. تصور کنید که هر ناظری میتواند ۱۰ کارگر خط تولید را و هر مدیری ۱۰ ناظر را سرپرستی کند. اگر بنگاه اقتصادی ۱۰ کارگر خط تولید استخدام کند آنوقت مالک میتواند مدیریت و نظارت را خودش انجام دهد. اگر ۱۰۰ کارگر استخدام کند باید بتواند یک لایه ۱۰ نفری از ناظران داشته باشد. و اگر تا حد ۱۰۰۰ کارگر رشد کند، باید بتواند یک لایه مدیریتی دیگر برای نظارت بر ناظران داشته باشد. بهاین ترتیب، افزایش تعداد کارگران خط تولید مستلزم آن است که نظارت و مدیریت با نسبتی بیش از آن افزایش پیدا کنند. تنها راه بنگاه اقتصادی برای اینکه افزایش ورودیها را به یک نسبت یکسان حفظ کند این است که از شدت نظارت خود بکاهد که این هم بهنوبه خود بهره وری را کاهش خواهد داد. ما این عدم صرفه جویی ناشی از مقیاس را (به پیروی از این کمیک استریپ قانون سلسله مراتب شرکتی دیلبِرت, کمیک استریپ دیلبرت)مینامیم. در قسمت انیشتین پایان این فصل خواهید دید که عدم صرفه جویی ناشی از مقیاسی که قانون دیلبرت بدنبال دارد را چگونه باید محاسبه کرد.
مزایای ناشی از هزینه
- تحقیق و توسعه
- هزینهکردهایی که توسط یک نهادِ خصوصی یا عمومی برای ایجاد روشهایی تولیدِ تازه، محصولات یا هرگونه دانشِ به لحاظِ اقتصادی مرتبط انجام میشود.
هرچه بنگاه اقتصادی تولید بیشتر داشته باشد، هزینه هر واحد کاهش پیدا میکند، حتی اگر بازگشت به مقیاس ثابت و یا کاهشی باشد. این اتفاق زمانی میافتد که هزینه ثابتی در میان باشد که مستقل از تعداد واحدها است – یعنی چه بنگاه اقتصادی یک واحد تولید کند چه چند واحد، این هزینه یکسان خواهد بود. یک نمونه هزینههای مربوط به تحقیق و توسعه (R&D) و طراحی محصول است که برای اخذ مجوز تولید یا دریافت حق انحصاری ثبت یک تکنیک خاص لازم است. هزینههای بازاریابی از قبیل تبلیغات نمونه دیگری از هزینههای ثابت هستند. هزینه یک تبلیغ ۳۰ ثانیهای در حین پوشش تلویزیونی مسابقات فوتبال سوپر بول آمریکا در سال ۲۰۱۴ برابر با ۴ میلیون دلار بوده است؛ این هزینه زمانی توجیه خواهد داشت که فروشی با تعداد بسیار بالا را در پی داشته باشد.
هزینه تلاش بنگاه اقتصادی و لابیگری برای اینکه از سوی بدنههای دولتی برخورد مناسبی دریافت کند، یا مشارکت در کارزارهای انتخاباتی، و یا هزینههای مربوط به روابط عمومی نیز از جمله هزینههای ثابت محسوب میشوند. اینها هزینههایی هستند که کم و بیش مستقل از سطح خروجی بنگاه اقتصادی باید تأمین شوند.
دوم اینکه بنگاههای اقتصادی بزرگ میتوانند ورودیهای موردنیاز خود را با شرایط مطلوبتری خریداری کنند، چرا که در مذاکره با تأمینکنندگان، نسبت به بنگاههای اقتصادی کوچکتر، از قدرت چانهزنی بالاتری برخوردارند.
مزایای ناشی از تقاضا
- صرفهجوییِ شبکهای ناشی از مقیاس
- این حالت وقتی اتفاق میافتد که افزایشِ شمار کاربرانِ خروجیِ یک شرکت، به دلیلِ اینکه این کاربران با یکدیگر پیوند دارند، افزایش ارزشِ خروجی برای هریک از آنها را در پی دارد.
حجم زیاد نه تنها در فرآیند تولید، بلکه در فروش محصول هم میتواند به بنگاه اقتصادی سود برساند. این اتفاق زمانی میافتد که یک محصول یا خدمات، بهدلیل اینکه از قبل کاربران زیادی دارد، احتمال فروش بیشتری دارد. برای مثال یک اپلیکیشن نرم افزاری وقتی که همه از یک نسخه انطباق پذیر آن استفاده میکنند کاربرد بیشتری دارد. این مزایای ناشی از مقیاس برخاسته از نیمه ی تقاضا را صرفه جویی شبکهای ناشی از مقیاس مینامیم و نمونههای بسیاری از آن در بازارهای مربوط به فناوری دیده میشود.
ازآنجا که تولید در حجم بالا صرفه جویی ناشی از مقیاس ایجاد میکند، هزینهها را کاهش و تقاضا را بالا میبرد، تولید کلان-مقیاس تأثیر نیرومندی بر اندازه بنگاه اقتصادی دارد. تولید با تعداد اندکی از افراد، غالباً بسیار پرهزینهتر از آن است که بتواند با بنگاههای اقتصادی بزرگتر رقابت کند.
بنگاههای اقتصادی کوچک عموماً میمیرند یا رشد میکنند، اما رشد بنگاههای اقتصادی هم حد و اندازهای دارد. پیش از این در فصل ۶ دیدهایم که بنگاههای اقتصادی میتوانند تولید قطعاتشان را برون سپاری کنند. رشد بنگاه اقتصادی حدی دارد و این تا حدی بدین دلیل است که گاهی بنگاه اقتصادی میتواند بخشی از محصولی را که خود باید تولید کند به قیمت ارزانتری بخرد. اپل اگر تصمیم میگرفت بهجای اینکه صفحات لمسی و چیبست و دیگر قطعات تشکیلدهنده آیفون و آیپد را که از توشیبا، سامسونگ و دیگر شرکت های تولیدکننده قطعات اپل میخرد، توسط کارمندان خودش تولید کند، احتمالاً اندازه غول آسایی پیدا میکرد. راهبرد برون سپاری اپل اندازه بنگاه اقتصادی را محدود میکند، و بر اندازه شرکتهایی چون توشیبا و سامسونگ و دیگر تولیدکنندههای قطعات اپل میافزاید.
در قسمت بعدی الگویی بدست خواهیم داد از اینکه چگونه هزینههای بنگاه اقتصادی تابع مقیاس تولید آن است.
پرسش ۷.۴ (همه پاسخهای صحیح را انتخاب کنید).
کدامیک از گزاره های زیر صحیح است؟
- (الف) وقتی بازگشتِ ثابت داریم، هر افزایش ورودی، به افزایشی به همان میزان در خروجی میانجامد.
- (ب) وقتی بازگشتِ کاهشی داریم، دو برابر کردن سطحِ ورودی، به کمتر از دو برابر شدن سطحِ خروجی میانجامد.
- (ج) از آنجا که شرکت میتواند افزایشی در خروجی داشته باشد که با افزایشی کمتر از آن در ورودی بدست میآید، هزینه شرکت برای هر قطعه یا واحد هم کاهش پیدا میکند.
- (د) وقتی بازگشتِ کاهشی داریم، افزایشِ ورودی به افزایشی کمتر از آن در خروجی میانجامد.
انیشتین اندازه و هزینه یک لوله
با استفاده از یک ریاضیات بسیار ساده میتوانیم پیدا کنیم که هزینه ساخت یک لوله وقتی که مساحت سطح مقطع آن دو برابر میشود. فرمول محیط دایره به قرار زیر است:
فرض کنیم که مساحت لوله در ابتدا ۱۰ cm2 بوده است، و سپس اندازه آن دو برابر شد یعنی ۲۰ cm2. میتوانیم از معادله فوق برای پیدا کردن شعاع لوله در هر مورد استفاده کنیم.
وقتی که مساحت لوله ۱۰ است:
وقتی که مساحت لوله ۲۰ است:
هزینه مواد اولیه لازم برای ساخت لولهای با طول مشخص، تابع محیط آن است. فرمول محیط دایره بهقرار زیر است:
وقتی که مساحت دایره ۱۰ است:
وقتی که مساحت دایره ۲۰ است:
ظرفیت لوله دو برابر شده است، اما محیط و بنابراین هزینه آن، تنها به صورت ضریبی رشد کرده است.
از همین جا میتوان دید که بنگاه اقتصادی از صرفه جویی ناشی از مقیاس برخوردار شده است.
عدم صرفه جویی ناشی از مقیاس: قانون دیلبرتیِ CORE درباب سلسله مراتب شرکتی
اگر هر ده کارمند رده پایین بایستی یک ناظر در یک سطح بالاتر داشته باشند، آنگاه بنگاه اقتصادیی که ۱۰x کارگر تولید (پایین نردبام) داشته باشد، x سطح مدیریت، ۱۰x-۱ ناظر در پایینترین سطح، ۱۰x−۲ ناظر در یک سطح پیش از آخرین سطح، و الی آخر خواهد داشت.
بنابراین بنگاه اقتصادیی با یک میلیون (۱۰۶) کارگر تولیدی۱۰۰۰۰۰ (۱۰۵ = ۱۰۶-۱) ناظرِ پایینترین سطح خواهد داشت. دیلبرتی این قانون را اختراع نکرد؛ کارفرمایش بیش از اینها او را زیر نظر داشت که وقتی برای اینکار پیدا کند. تیم CORE اختراع کرد.
۷.۳ تولید: تابع هزینه برای اتومبیلهای زیبا
برای تعیین قیمت و تعداد تولید اپل-سینامون چیروز، مدیر بنگاه اقتصادی نیاز داشت که تابع تقاضا و هزینههای تولید را بداند. ازآنجا که ما فرض میکنیم هزینه تولید هر پوند چیروز یکسان بوده است، پس مقیاس تولید تابع تقاضا برای این کالا است. در این فصل و فصل بعدی، مثالهای متفاوتی را بررسی خواهیم کرد که در آن هزینهها به موازات سطح تولید تغییر میکنند.
بنگاه اقتصادیی را در نظر بگیرید که اتومبیل تولید میکند. در مقایسه با شرکت فورد که سالانه ۶.۳ میلیون اتومبیل تولید میکند، این بنگاه اقتصادی اتومبیلهای خاص و سفارشی تولید میکند و همانطور که خواهیم دید نسبتاً کوچک است و ما آن را شرکت اتومبیلهای زیبا خواهیم نامید.
هزینههای تولید و فروش اتومبیل را در نظر بگیرید. بنگاه اقتصادی به تأسیساتی نیاز دارد (یعنی یک کارخانه) که به ماشین آلات لازم برای قالب ریزی، آهنگری، مونتاژ و جوشکاری قطعات اتومبیل مجهز باشد. حالا یا ممکن است این تأسیسات را از کارخانه ی دیگری قرض بگیرد یا اینکه سرمایه مالی خود را برای سرمایه گذاری در تأسیسات و تجهیزات بالا ببرد. سپس باید مواد و قطعات خام را خریداری کند، و برای راه اندازی و راه بردن تجهیزات کارگران تولیدی استخدام کند. کارگران دیگری هم برای مدیریت فرایند تولید، بازاریابی و فروش اتومبیلهای نهایی موردنیاز خواهند بود.
- هزینه فرصت
- ازآنجاکه انجام هر اقدامی به معنای پشتسرگذاشتنِ بهترین گزینه بعدی است، هزینه فرصت عبارت است از سودِ خالصِ ناشی از جایگزینِ پشتسرگذاشته شده.
- هزینهی فرصتِ سرمایه
- میزانِ درآمدی که یک سرمایهگذار میتوانسته با سرمایهگذاری یک واحدِ سرمایه در جایی دیگر بدست بیاورد.
مالکان بنگاه اقتصادی –سهامداران – اگر این امکان را داشته باشند که با سرمایه گذاری در جای دیگر استفاده بهتری از پولشان بکنند، تبعاً تمایلی به سرمایه گذاری در این بنگاه اقتصادی نخواهند داشت. آنچه بهواسطه هر یک دلار سرمایه گذاری در جای دیگر میتوانند کسب کنند، نمونه ی دیگری از هزینه فرصت (که در فصل ۳ بحث شد) است، که در این مورد آن را هزینه فرصت سرمایهگذاریمینامیم. بخشی از هزینه تولید اتومبیل، پولی است که باید به سهامداران پرداخت شود تا هزینه فرصت سرمایه گذاری شان جبران شود – یعنی ترغیب شوند که بازهم همچنان پول خود را در داراییهایی که بنگاه اقتصادی برای تولید اتومبیل نیاز دارد سرمایه گذاری کنند.
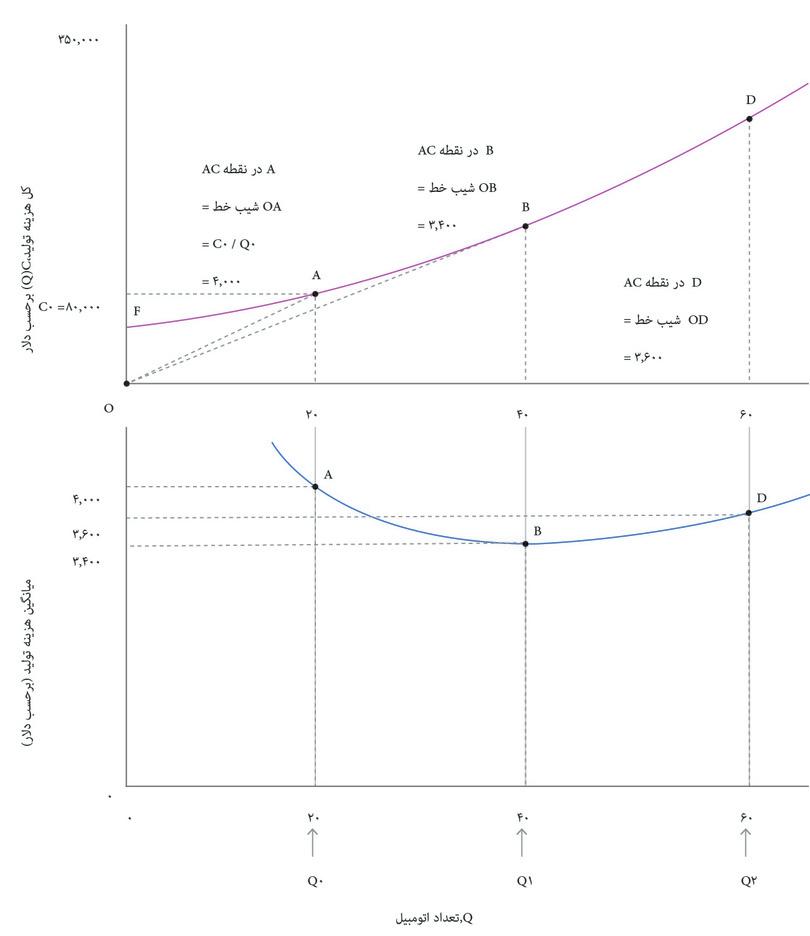
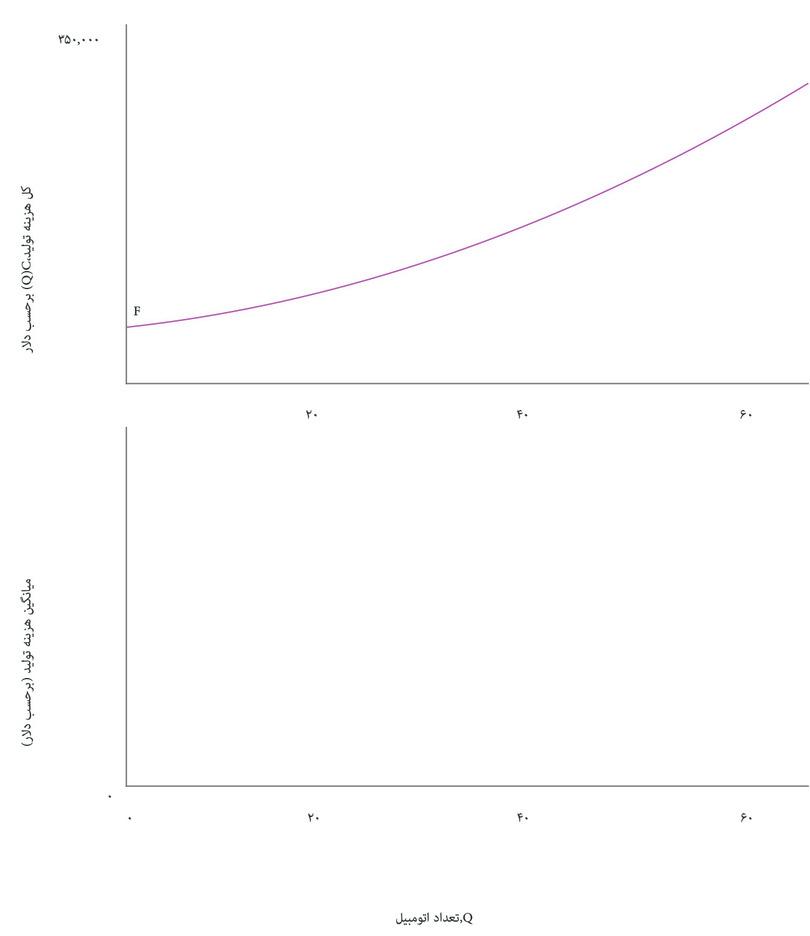
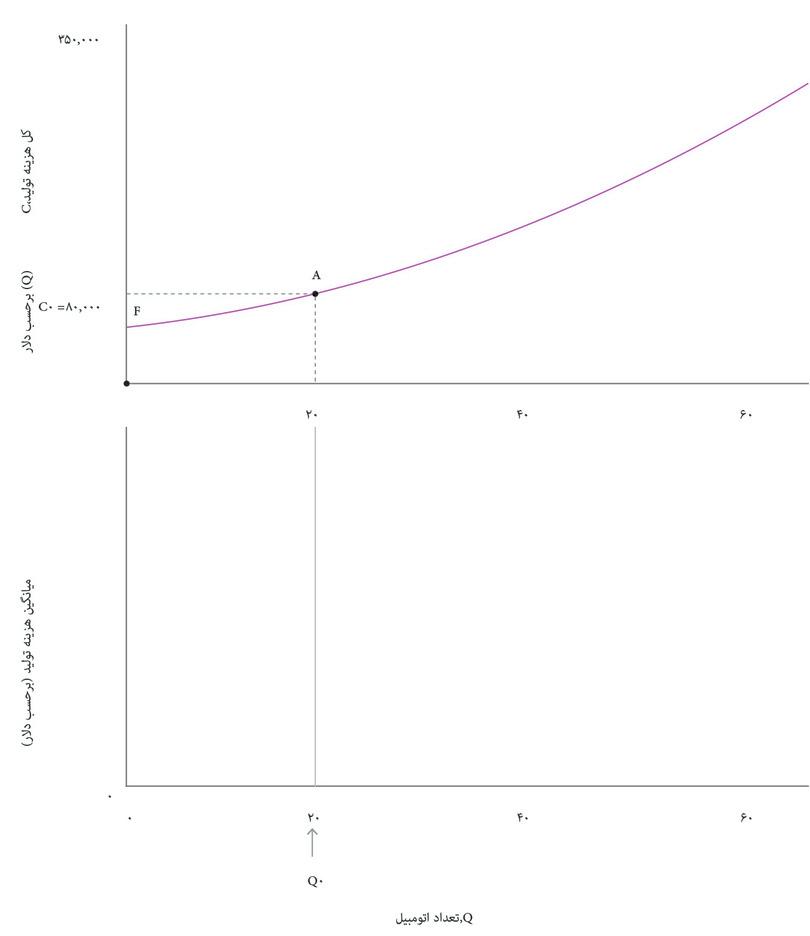
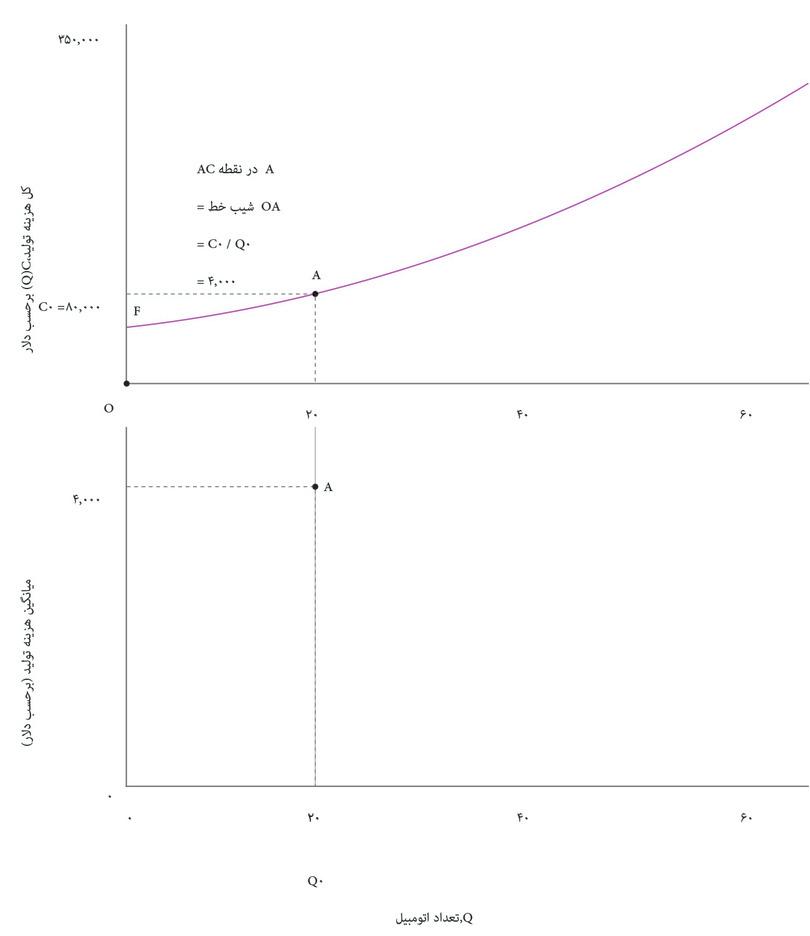
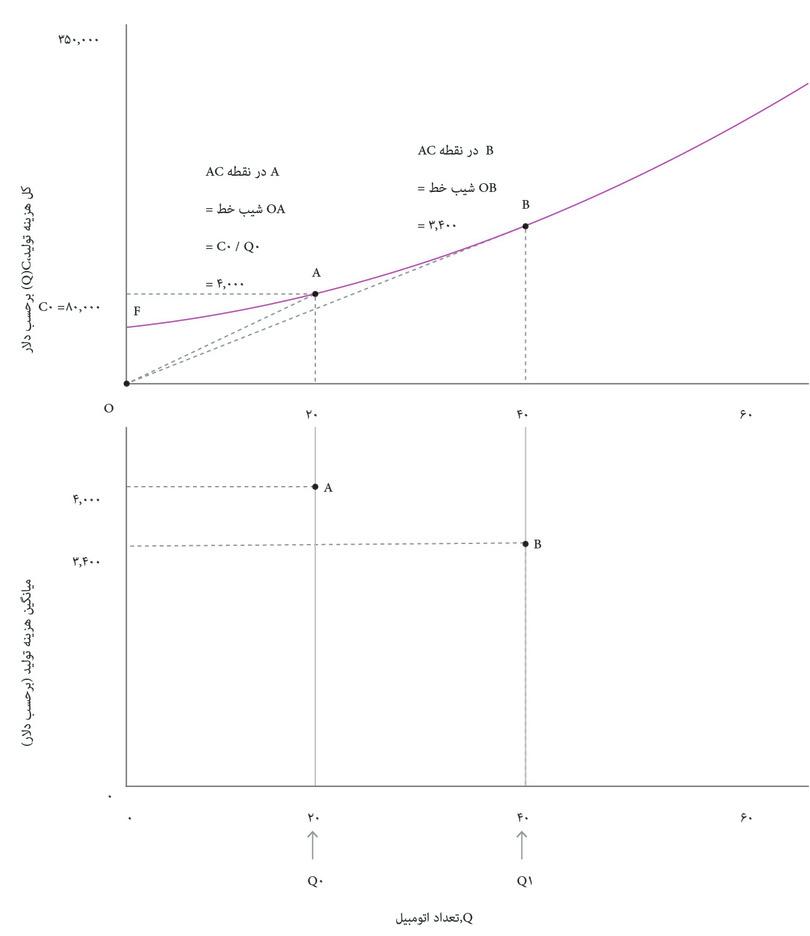
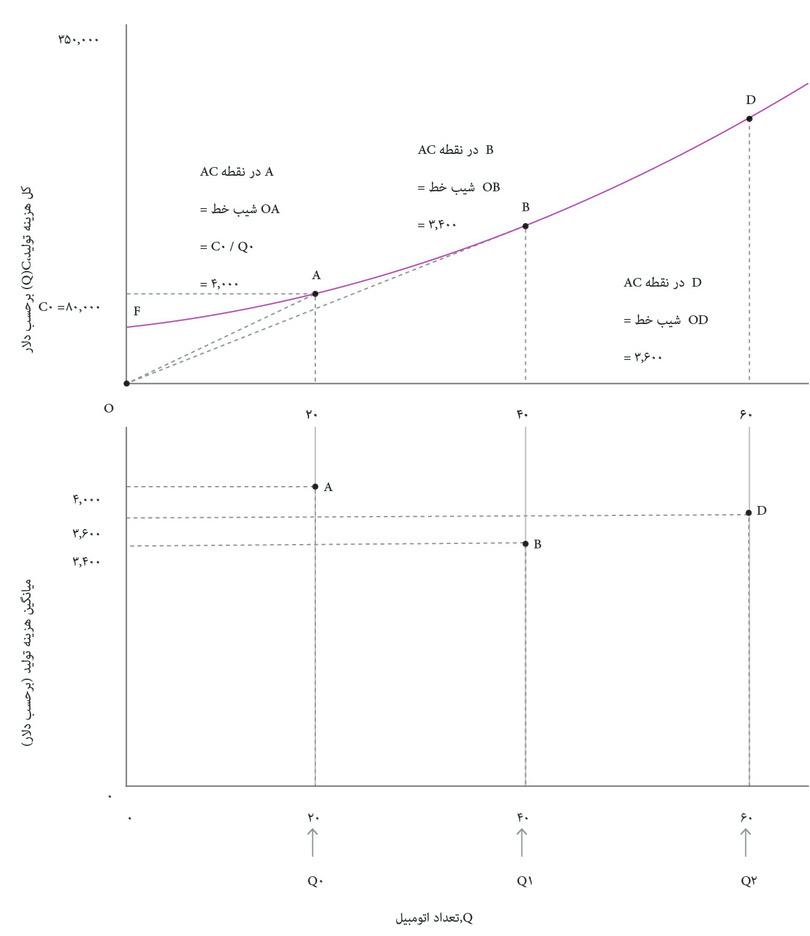
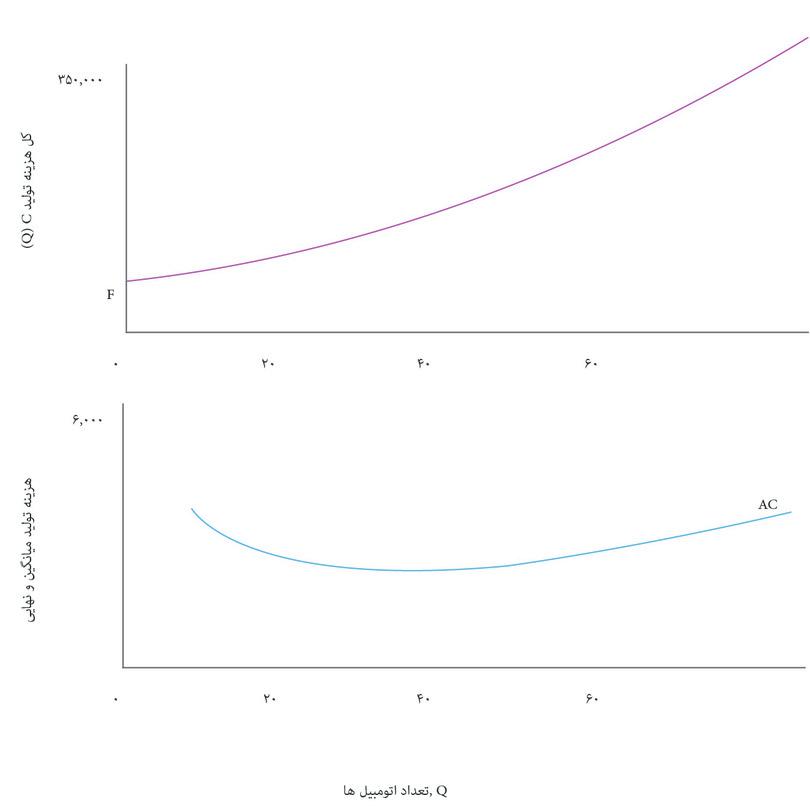
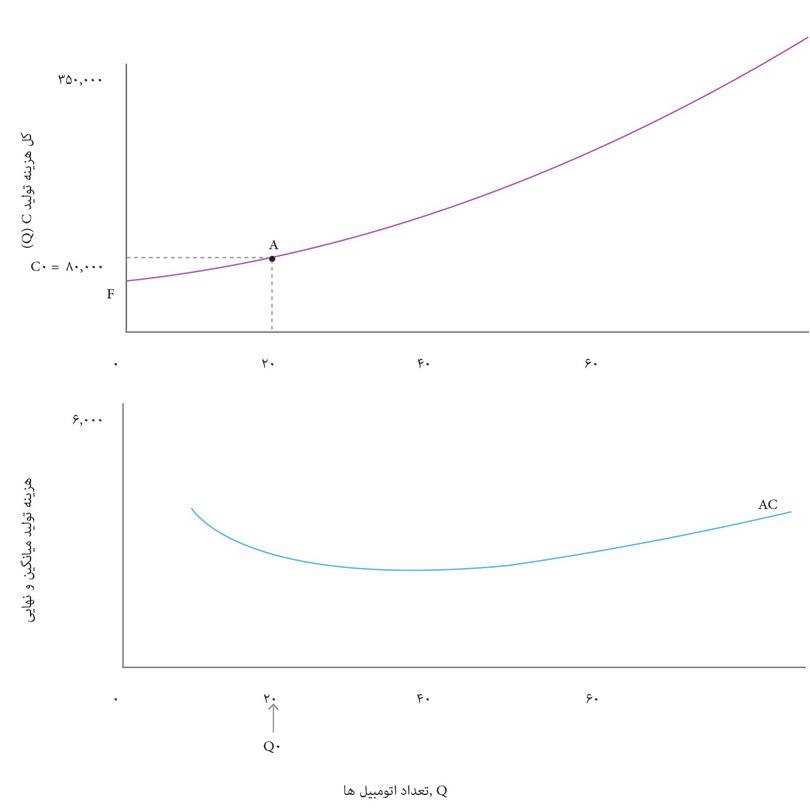
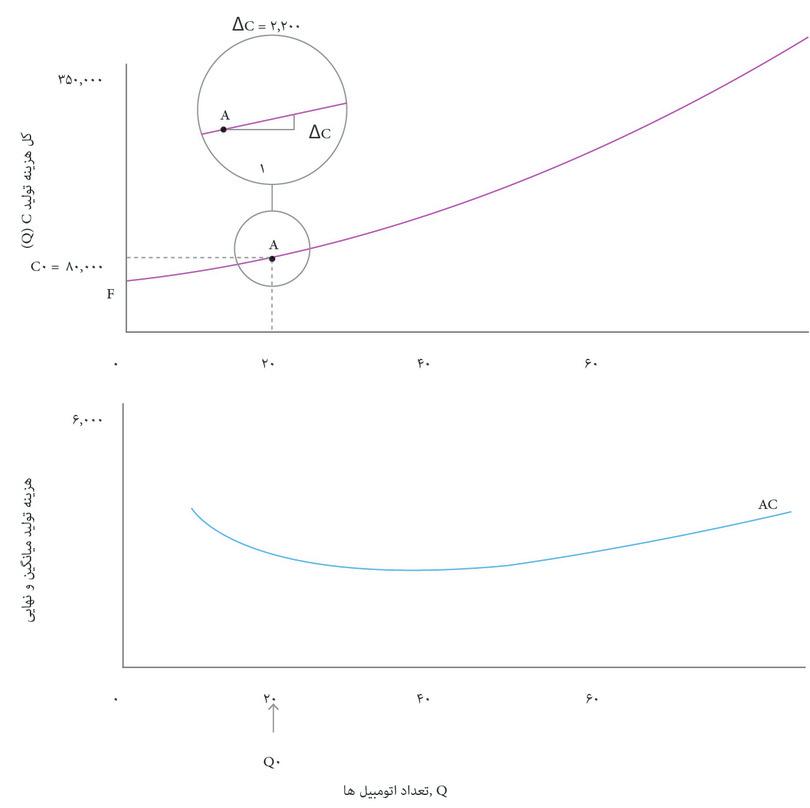
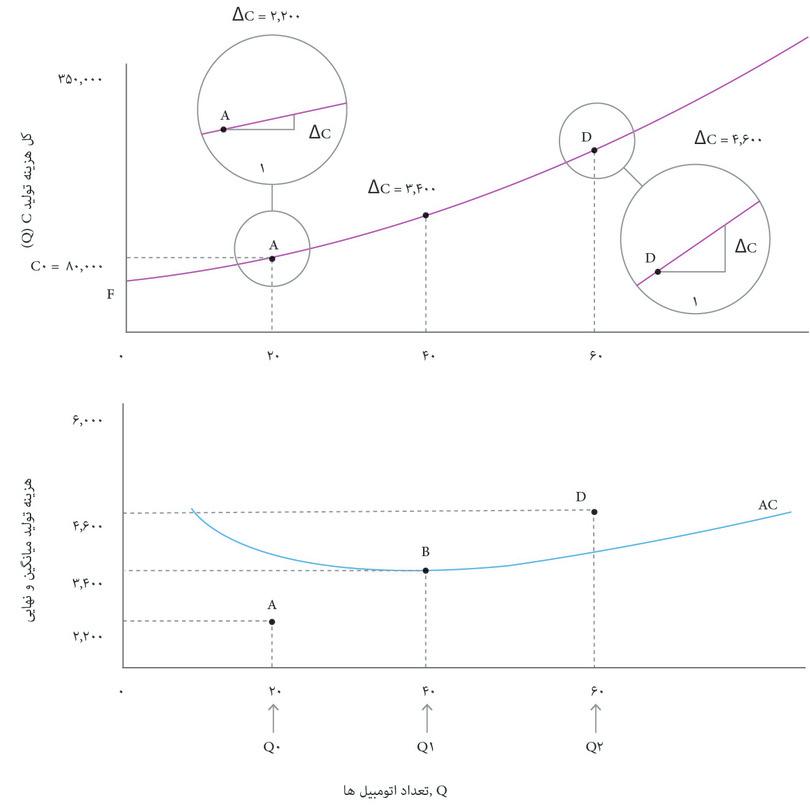
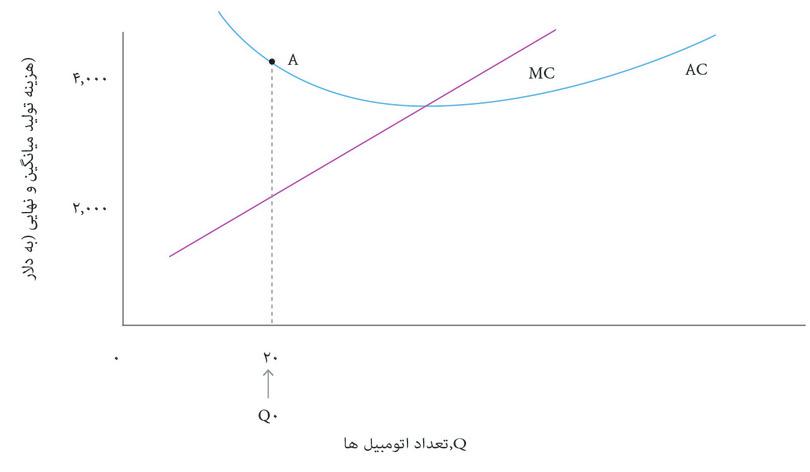
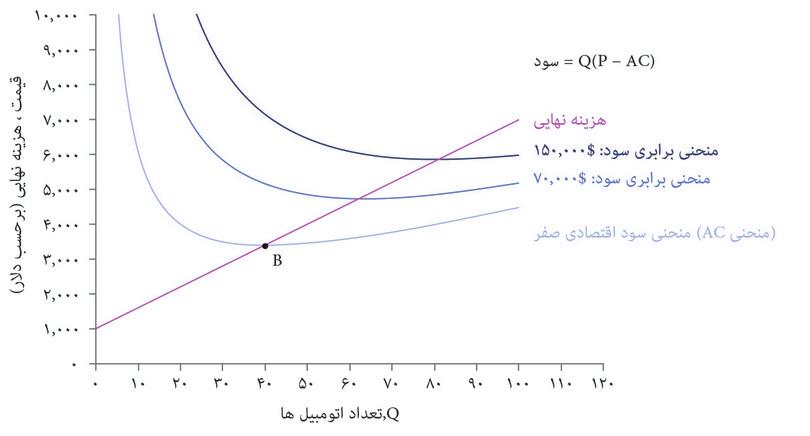
هرچه ماشین بیشتری تولید شود، کل هزینهها هم بالاتر خواهد بود. قاب بالایی شکل ۷.۶ نشان میدهد که چگونه کل هزینه به تعداد اتومبیل تولید شده، Q, در روز بستگی دارد. این تابع هزینه بنگاه اقتصادی یا C(Q).است. از روی تابع هزینه، میانگین هزینه یک اتومبیل، و اینکه چگونه این هزینه برحسب تعداد، Q تغییر میکند را استخراج کردهایم؛ منحنی میانگین هزینه (AC) در قاب پایینی ترسیم شده است.
- هزینههای ثابت
- هزینههای تولیدی که به موازاتِ تعداد واحدهای تولیدشده تغییر نمیکنند.
در شکل ۷.۶ میبینیم که در سطح تولید پایین، میانگین هزینه کاهشی دارد: منحنی AC شیب رو به پایین دارد. اما در سطح تولید بالا، میانگین هزینه افزایش مییابد بطوری که شیب منحنی AC رو به بالا میشود. دلیل این مسأله ممکن است این باشد که بنگاه اقتصادی باید تعداد شیفهای کاری روزانه در خط تولید را افزایش دهد. شاید مجبور است اضافه کار پرداخت کند یا خرابی تجهیزات وقتی خط تولید زمان طولانیتری کار میکند بالاتر رفته است.
هزینه نهایی
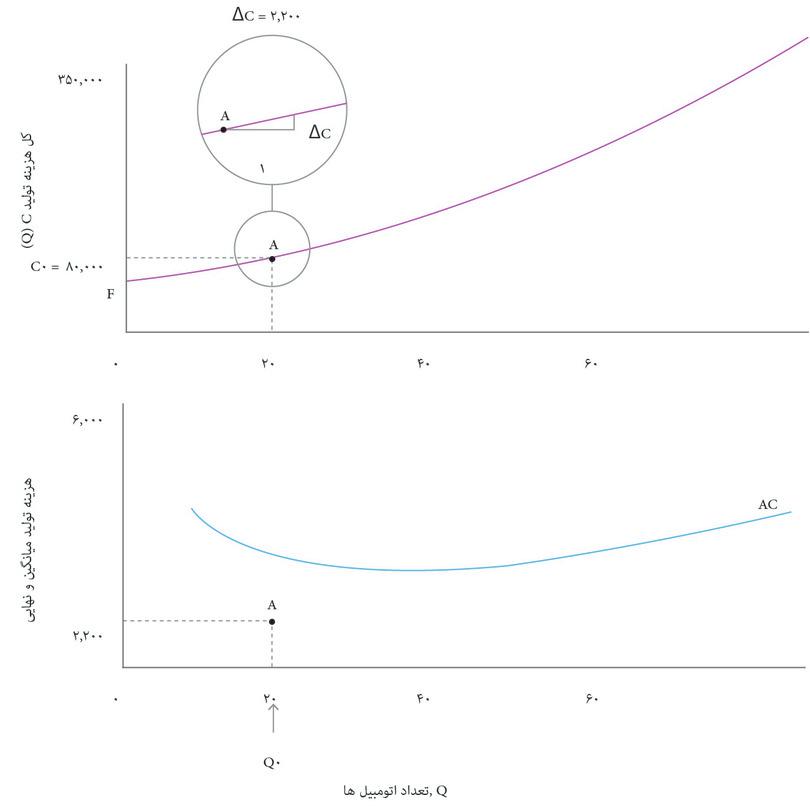
در هر نقطه روی تابع هزینه، هزینه نهایی (MC) همان هزینه اضافی تولید یک واحد خروجی بیشتر است، که متناظر با شیب تابع هزینه است. اگر هزینه به اندازه ∆C تغییر کند، در حالی که تعداد به اندازه ∆Q, تغییر کرده است، آنگاه هزینه نهایی را میتوان بهاین شیوه محاسبه کرد:
- هزینه نهایی
- تأثیرِ ناشی از کلِ هزینه تولیدِ یک واحدِ اضافی از خروجی. که برابر است با شیبِ تابعِ کلِ هزینه در هر نقطه.
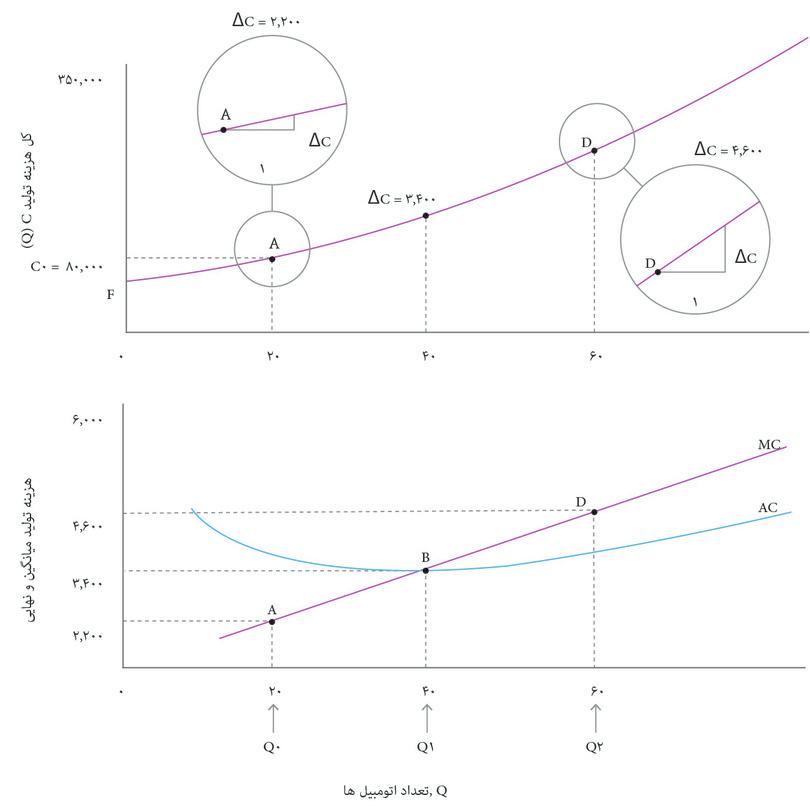
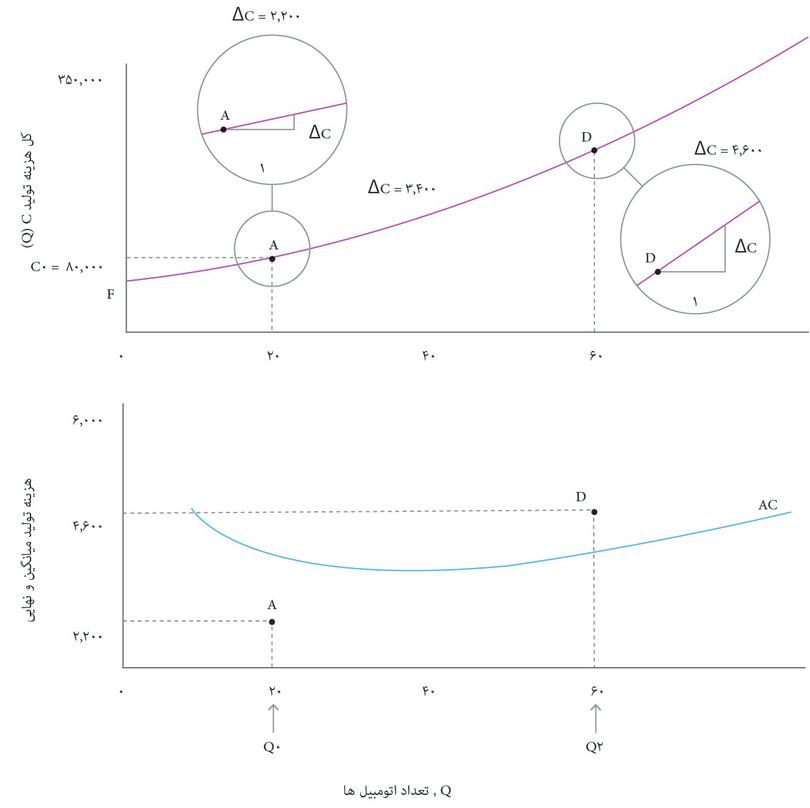
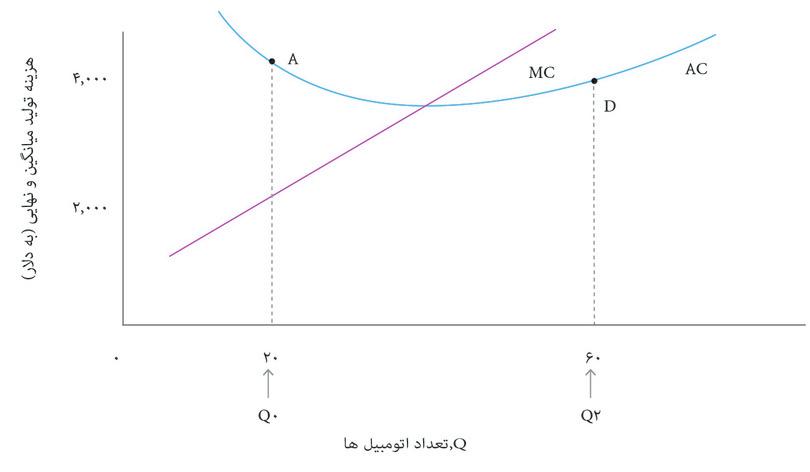
شکل ۷.۷ نشان میدهد که چگونه هزینه نهایی یک اتومبیل را پیدا کنیم: یعنی هزینه تولید یک اتومبیل بیشتر. در فصل ۳ دیدیم که تولید نهایی برای یک تابع تولید معلوم، عبارت است از خروجی اضافیای که با افزایش یک واحدی به ورودی تولید میشود که به شیب تابع تولید بستگی دارد. شکل ۷.۷ نیز بههمین شیوه، نشان میدهد که هزینه نهایی (MC) متناظر با شیب تابع تولید است.
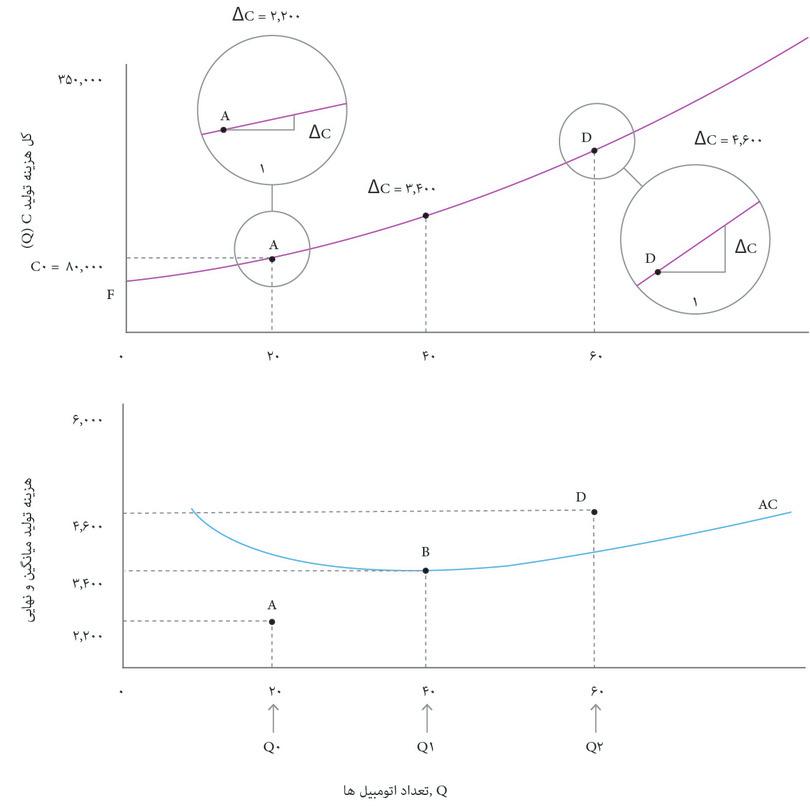
ازآنجا که هزینه نهایی همان شیب تابع هزینه است و منحنی هزینه با بالارفتن تعداد، Q, تختتر میشود، نمودار هزینه نهایی خطی با شیب رو به بالا خواهد بود. بهعبارت دیگر، شرکت اتومبیلهای زیبا با روند افزایشی هزینه نهایی تولید اتومبیل روبهرو است. همین هزینه نهایی افزایشی است که به یکباره باعث افزایش میانگین هزینه میشود.
توجه داشته باشید که در شکل ۷.۷ هزینه نهایی را بهاین شکل پیدا کردیم: تغییر هزینه ∆C, ناشی از تولید یک اتومبیل بیشتر. گاهی راحتتر است که تغییر متفاوتی در تعداد را در نظر بگیریم. اگر بدانیم که با تولید ۵ اتومبیل بیشتر، هزینهها بهاندازه ∆C = $۱۲۰۰۰ افزایش پیدا میکنند، آنگاه میتوانیم ∆C/∆Q, را در شرایطی که ∆Q = ۵، باشد محاسبه کنیم تا به برآوردی از هزینه نهایی ۲۴۰۰ دلاری بهازای هر اتومبیل برسیم. بطورکلی وقتی تابع هزینه از انحنا برخوردار است، ∆Q کوچکتر، برآورد دقیقتری را به ما میدهد.
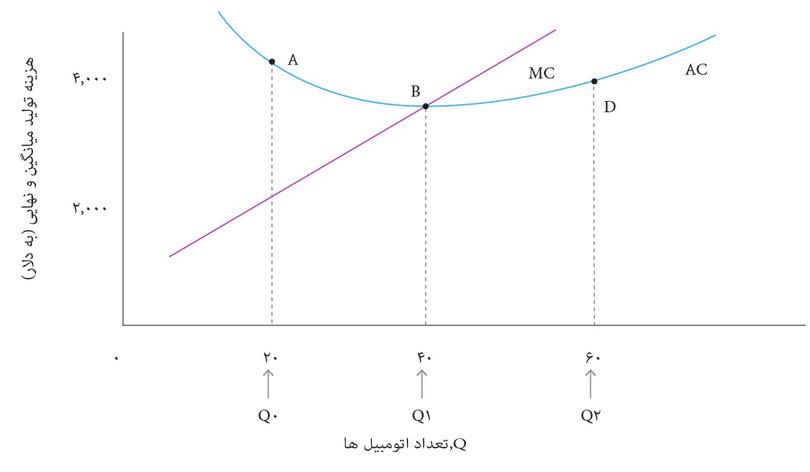
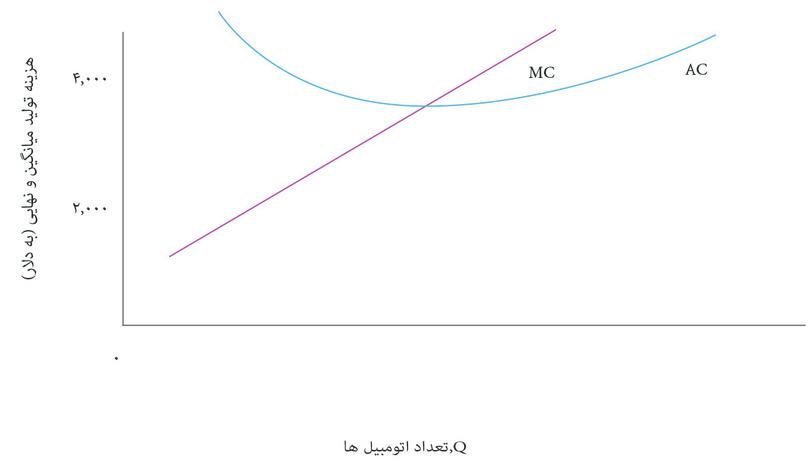
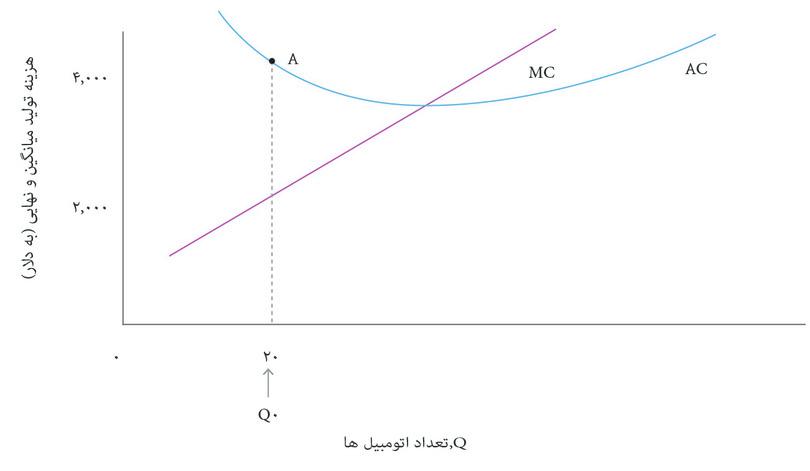
حالا بهشکل منحنیهای AC و MC که دوباره در شکل ۷.۸ نشان داده شده اند نگاه کنید. ملاحظه میکنید که در ارزشهایی از AC که بزرگتر از MC است، شکل AC شیب رو به پایین نشان و آنجاکه AC کمتر از MC است شیب رو به بالا دارد. این صرفاً یک تصادف نیست: شکل تابع هزینه کل هر چه باشد بازهم این اتفاق خواهد افتاد. با رجوع به خطوط کناره ببینید که چرا چنین اتفاقی میافتد.
لایبنتیز: توابع هزینه میانگین و نهایی
پرسش ۷.۵ (یک پاسخ را انتخاب کنید)
شرکتی با هزینههای تولید ثابت را در نظر بگیرید. کدامیک از گزارههای زیر درباب هزینه میانگین (AC) و هزینه نهایی (MC) آن درست است؟
- وقتی AC = MC است، هزینه یک واحد اضافی برابر است با هزینه میانگین همه واحدهای موجود. بنابراین، AC جدید یکسان و شیب تغییری نخواهد کرد.
- منحنی MC می تواند، فارغ از اندازه نسبی AC و MC، شیب رو به بالا داشته باشد، افقی باشد یا شیب رو به پائین داشته باشد.
- وقتی AC < MC است، هزینه یک واحد اضافی بزرگتر از میانگین هزینه خروجیهای موجود است. بنابراین AC جدید بزرگتر خواهد بود، یعنی منحنی AC شیب رو به بالا خواهد داشت.
- اگر MC ثابت باشد، منحنی MC افقی خواهد بود.
پرسش ۷.۶ (یک پاسخ را انتخاب کنید).
فرض کنید که هزینه تولیدِ یک پوند غله، صرفنظر از سطح خروجی، 2 دلار است. کدامیک از گزارههای زیر صحیح است.
- کل هزینه عبارت است از ۲ Q در حالی که Q خروجی است. این یک خط مستقیم رو به بالا است که از نقطه مبدأ میگذرد.
- هزینه میانگین = ۲ برای هر خروجیای. این یک خط مستقیم افقی است.
- هزینه نهایی = ۲ برای هر خروجیای. این یک خط مستقیم افقی است.
- هم هزینه میانگین و و هم هزینه نهایی برای همه خروجیها برابر با 2 است، بنابراین منحنی هایی که آنها را نشان میدهند، هم را قطع میکنند.
تمرین ۷.۲ تابع هزینه برای اپل-سینامون چیروز
البته توابع هزینه اشکال متفاوتی نسبت به چیزی که برای اتومبیلهای زیبا استخراج کردهایم، خواهند داشت. برای اپل-سینامون چیروز، فرض کردیم که هزینهای دانهای هر پوند غله، صرفنظر از کمیت تولید، برابر با ۲ دلار است. این بدان معناست که میانگین هزینه ثابت بوده است.
- سعی کنید تابع هزینه برای این مورد را رسم کنید.
- توابع هزینه نهایی و میانگین چه شکلی دارند؟
- حالا فرض کنید که هزینه نهایی تولید یک پوند چیروز، صرفنظر از تعداد تولید، ۲ دلار است، اما هزینههای تولیدی ثابت هم وجود دارند. سعی کنید که توابع هزینه کل، نهایی و میانگین را در این مورد رسم کنید.
- صرفهجویی ناشی از دامنه
- صرفهجویی در هزینهای که وقتی دو یا چند کالا بجای اینکه در چند شرکت جداگانه تولید شوند توسط یک شرکت تولید میشوند، ایجاد میشود.
دو اقتصاددان بنامهای راجیندَر و منجولیکا کوشَل، توابع هزینه دانشگاههای ایالات متحده را محاسبه کردند.3آنها هزینه نهایی و میانگین آموزش دانشجویان تحصیلات تکمیلی و پایینتر را در ۱۷۱ دانشگاه دولتی در سال تحصیلی ۹۱-۱۹۹۰را برآورد کردند. همانطور که در تمرین ۷.۳ خواهید دید، آنها با میانگین هزینه کاهشی روبهرو شدند. همچنین متوجه شدند که دانشگاهها از چیزی که میتوان آن را صرفه جویی ناشی از دامنه: نامید بهره مند میشوند: یعنی صرفهجوییهایی در هزینه وجود دارند که از تولید همزمان چند محصول – در این مورد تحصیلات تکمیلی، تحصیلات پایه، و تحقیقات - ناشی میشوند.4
اگر میخواهید در مورد هزینهها بیشتر بدانید، جرج استیگلر اقتصاددان، بحث جذابی در همین مورد را در فصل ۷ همین کتاب نوشته است که بصورت آنلاین هم در دسترس است.5
تمرین ۷.۳ توابع هزینه برای تحصیل دانشگاهی
در زیر میتوانید هزینه نهایی و میانگین هر دانشجو برای سال ۹۱-۱۹۹۰ که کوشل و کوشل براساس پژوهش خود محاسبه کرده اند را ببینید.
دانشجویان MC ($) AC ($) کل هزینه($) کارشناسی ارضد ۲۷۵۰ ۷۲۵۹ ۷۶۵۹ ۲۱، ۰۶۲،۲۵۰ ۵۵۰۰ ۶۵۴۸ ۷۳۴۸ ۴۰، ۴۱۴، ۰۰۰ ۸۲۵۰ ۵۸۳۸ ۷۰۳۸ ۱۱۰۰۰ ۵۱۲۵ ۶۷۲۷ ۷۳، ۹۹۷،۰۰۰ ۱۳۷۵۰ ۴۴۱۷ ۶۴۱۷ ۸۸، ۲۳۳، ۷۵۰ ۱۶۵۰۰ ۳۷۰۶ ۶۱۰۶ ۱۰۰،۷۴۹،۰۰۰ دانشجویان MC ($) AC ($) کل هزینه ($) فارغ التحصیلان ۵۵۰ ۶۵۴۱ ۱۲۱۴۰ ۶،۶۷۷،۰۰۰ ۱۱۰۰ ۶۸۲۱ ۹۴۵۴ ۱۰،۳۳۹،۴۰۰ ۱۶۵۰ ۷۱۰۲ ۸۶۷۲ ۲۲۰۰ ۷۳۸۳ ۸۳۶۵ ۱۸،۴۰۳،۰۰۰ ۲۷۵۰ ۷۶۶۴ ۸۲۴۹ ۲۲،۶۸۴،۷۵۰ ۳۳۰۰ ۷۹۴۵ ۸۲۲۸ ۲۷،۱۵۲،۴۰۰
- هزینههای میانگین با افزایش شمار دانشجویان چه تغییری میکند؟
- با استفاده از دادههای مربوط به میانگین هزینه، خانههای خالی در ستون هزینه کل را پر کنید.
- منحنیهای هزینه نهایی و هزینه میانگین برای آموزش پایه را روی یک نمودار رسم کنید: هزینهها را روی محور عمودی و تعداد دانشجویان را روی محور افقی نمایش دهید. نمودارهای متناظر با آن برای دانشجویان تحصیلات تکمیلی را روی یک نمودار جداگانه رسم کنید.
- شکل توابع کل هزینه برای دانشجویان پایه و تکمیلی چه شکلی از خود نشان میدهند؟ (میتوانید اینکار را با استفاده از دانستههای خود درباره هزینههای نهایی و میانگین انجام دهید، یا اینکه بطور دقیقتر براساس ستونهای هزینه کل رسم کنید. نکته: این توابع خط مستقیم نیستند).
- مهمترین تفاوتهای میان ساختار هزینهای دانشگاهها برای دانشجویان پایه و تکمیلی کدامند؟
- آیا تبیینی برای شکل نمودارهایی که رسم کرده اید به ذهنتان میرسد؟
۷.۴ منحنیهای تقاضا و برابری سود ماشینهای زیبا
- محصول متمایز
- محصولی که تنها توسط یک شرکت تولید میشود و در مقایسه با محصولات مشابه سایر شرکتها از خصوصیاتِ یگانهای برخوردار است.
همه اتومبیلها یکسان نیستند. اتومبیلها محصولات متمایزو خاصی هستند. هر سازه و الگو تنها توسط یک بنگاه اقتصادی تولید میشود و بهلحاظ طراحی و عملکرد ویژگیهای خاصی دارد که آن را از اتومبیلهای دیگر بنگاههای اقتصادی متمایز میکند.
انتظار داریم بنگاه اقتصادیی که محصول متمایزی را میفروشد، منحنی تقاضایی با شیب کاهشی داشته باشد. پیش از این یک مثال تجربی آن را در مورد اپل-سینامون چیروز (که آن هم یک محصول متمایز است) دیدهایم. اگر قیمت یک اتومبیل زیبا بالا باشد، تقاضا برای آن پایین خواهد بود، زیرا تنها مشتریانی که آن را خواهند خرید کسانی هستند که اتومبیلهای زیبا را شدیداً به همه سازههای دیگر ترجیح میدهند. اما با افت قیمت، مشتریان بیشتری، یعنی کسانی که در غیر این صورت ممکن بود فورد یا ولوو بخرند، جذب اتومبیل زیبا خواهند شد.
منحنی تقاضا
بهازای هر محصولی که مشتریان ممکن است تمایل به خرید آن داشته باشند، منحنی تقاضای محصول رابطهای است که تعداد اقلام (یا کمیتی) را که آنها با هر قیمت ممکن خواهند خرید به شما میگوید. برای اینکه الگوی سادهای از تقاضا برای اتومبیلهای زیبا بسازیم، فرض کنید که ۱۰۰ مصرف کننده بالقوه وجود دارند که درصورتی که قیمت بهاندازه کافی پایین باشد، هر کدام یک اتومبیل زیبا را امروز خواهند خرید.
- تمایل به پرداخت
- شاخصی از اینکه یک فرد چه مقدار برای یک کالا ارزش قائل است، و سنجه آن حداکثر مبلغی است که او حاضر است برای دستیابی به یک واحد از آن کالا بپردازد. همچنین نگاه کنید به: تمایل به قبول.
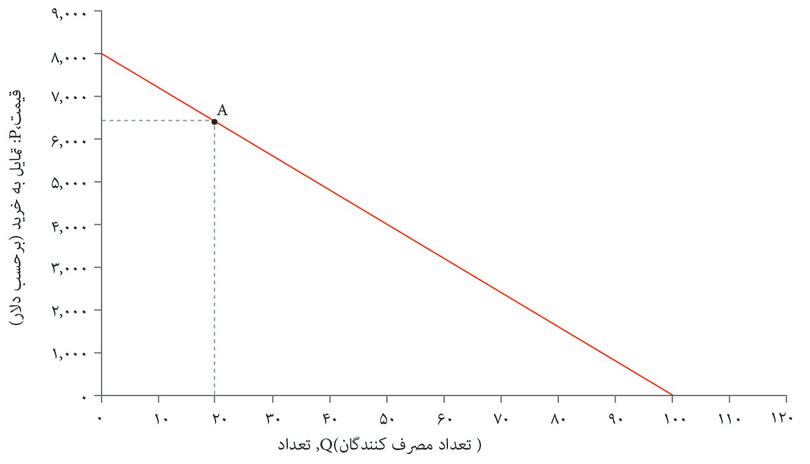
هر مصرف کنندهای یک تمایل به خرید (WTP) در مورد اتومبیلهای زیبا دارد که بستگی دارد به اینکه آن مصرف کننده شخصاً (و البته با توجه به منابعی که برای خرید دارد) چقدر برای آن ارزش قائل است. یک مصرف کننده وقتی ماشینی را میخرد که قیمت آن کمتر یا برابر با تمایل به خرید (WTP) او باشد. فرض کنید که مصرف کنندهها را بر اساس تمایل به خریدشان، از زیاد به کم، مرتب کنیم، و نموداری رسم کنیم که نشان دهد تمایل به خرید چگونه به موازات خط تغییر میکند (شکل ۷.۹). آنگاه، هر قیمتی را که انتخاب کنیم، مثلاً P = $۳۲۰۰نمودار تعداد مصرفکنندگانی را که تمایل به خریدشان بالاتر یا برابر با Pاست را نشان خواهد داد. در این مورد ۶۰ مصرف کننده تمایل دارند ۳۲۰۰ دلار یا بیشتر پرداخت کنند، پس تقاضا برای اتومبیل با قیمت ۳۲۰۰ دلار، برابر با ۶۰ است.
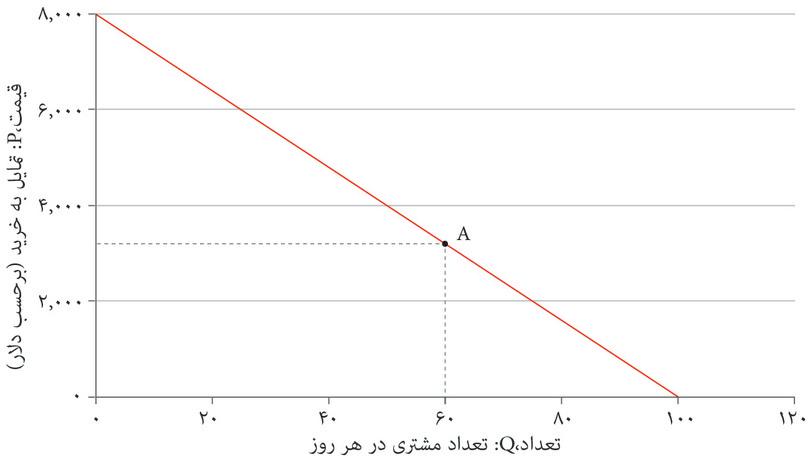
شکل ۷.۹ تقاضا برای اتومبیل (در روز)
اگر قیمت یا P پایینتر باشد، تعداد بیشتری از مصرفکنندگان تمایل به خرید دارند و بنابراین تقاضا بالاتر است. منحنیهای تقاضا را عموماً به شکل خطوط مستقیم رسم میکنند، اگرچه هیچ دلیلی وجود ندارد که انتظار داشته باشیم در عمل هم مستقیم باشند: دیدیم که منحنی تقاضا برای اپل-سینامون چیروز مستقیم نبود. اما انتظار داریم که منحنیهای تقاضا شیب کاهشی داشته باشند: یعنی با بالا رفتن قیمت، تعداد اتومبیلهایی که مشتریان سفارش میدهند کاهش پیدا میکند. بهعبارت دیگر، وقتی تعداد یا کمیت موجود پایین است، میتواند با قیمت بالایی فروخته شود. این رابطه میان قیمت و تعداد را گاهی تحت عنوان قانون تقاضا میشناسیم.
پیشینه قانون تقاضا به قرن هفدهم بر میگردد و به گریگوری کینگ (۱۶۴۸-۱۷۱۲) و شارل دِوِنان (۱۶۵۶- ۱۷۱۴) نسبت داده میشود. کینگ در کالجِ نظامی لندن یک مخبر بود و برآوردهای مبسوطی از جمعیت و ثروت انگلستان به عمل میآورد. دونان سیاستمداری بود که قانون تقاضای کینگ-دونان را با استفاده از دادههای کینگ در سال ۱۶۹۹ منتشر کرد. نوشته او توصیف میکرد که چگونه قیمت غله براساس حجم برداشت تغییر میکند. یک “کسری” دهدهی (یک دهم) قیمت را ۳۰ درصد افزایش میدهد و همینطور الی آخر:
پرسش ۷.۷ (همه پاسخهای صحیح را انتخاب کنید).
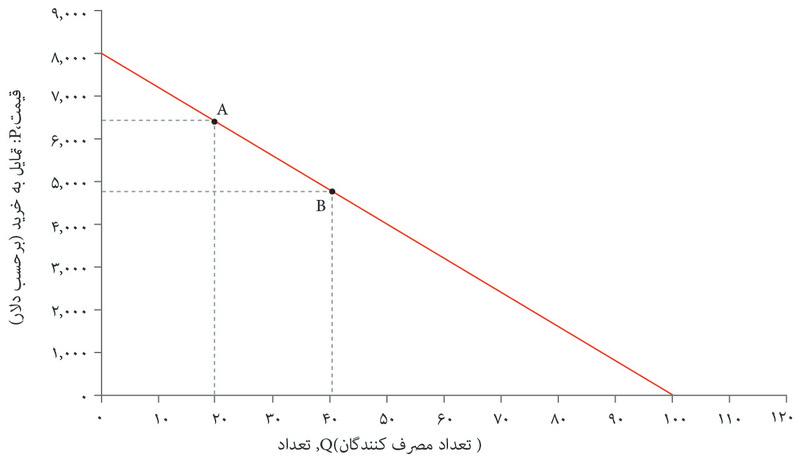
نمودار دو منحنی تقاضای جایگزین، یعنی D و D’ را برای یک محصول نشان می دهد. براساس نمودار کدامیک از گزاره های زیر صحیح است؟
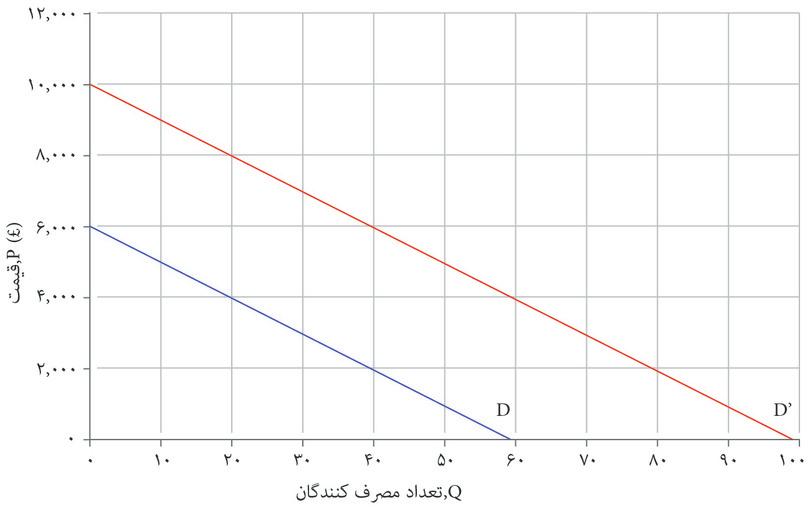
- (الف) روی منحنی تقاضای D، وقتی قیمت ۵۰۰۰ پوند است، شرکت می تواند ۱۰ واحد بفروشد.
- (ب) وقتی Q = ۷۰باشد، قیمت متناظر با آن روی D’، برابر با ۳۰۰۰ پوند است.
- (ج) منحنی D’ را می توان صرفاً نتیجه جابجایی منحنی به سمت راست به اندازه ۴۰ واحد درنظر گرفت.بنابراین بهازای هر قیمتی، شرکت میتواند روی D’، نسبت به D، ۴۰ واحد بیشتر بفروشد.
- (د) با خروجی ۳۰ واحد، شرکت می تواند روی D’، درمقایسه با D، ۴۰۰۰ پوند بیشتر قیمت بگذارد.
اتومبیلهای زیبا هم مثل تولیدکننده اپل-سینامون چیروز قیمت P, و تعداد Qرا با توجه به منحنی تقاضا و هزینههای تولید، انتخاب خواهد کرد. منحنی تقاضا، مجموعه مقرون بهصرفه ترکیبات قیمت و تعداد را مشخص میکند. برای پیداکردن نقطه حداکثر سود، منحنیهای برابری سود رسم میکنیم و طبق روال قبل به دنبال نقطه مماس میگردیم.
منحنیهای برابری هزینه:
سود بنگاه اقتصادی عبارت است از تفاوت درآمدهای آن (قیمت ضربدر تعداد فروش) و کل هزینههای آن یاC(Q):است:
- سود اقتصادی
- عوایدِ یک شرکت منهای کلِ هزینههای آن (منجمله هزینهی فرصتِ سرمایه).
- سودِ نرمال
- معادلِ سودِ اقتصادیِ صفر است و به این معنا است که نرخِ سود با هزینه فرصتِ سرمایه برابر است. همچنین نگاه کنید به: سودِ اقتصادی، و هزینه فرصتِ سرمایه.
این محاسبه چیزی را به ما میدهد که به آن سود اقتصادی میگوییم. فراموش نکنید که تابع هزینه، هزینه فرصت سرمایه (یعنی پرداختهایی که باید به مالکان انجام شود تا آنها را به حفظ سهامشان ترغیب کند) و به آن سودهای نرمال میگوییم را نیز در بردارد. سود اقتصادی عبارت است از سود اضافیای که علاوه بر حداقل بازگشت لازم برای سهامداران بدست میآید.
بهعبارت دیگر، سود عبارت است از تعداد واحدهای خروجی ضربدر سود هر واحد که تفاوت میان قیمت و میانگین هزینه است:
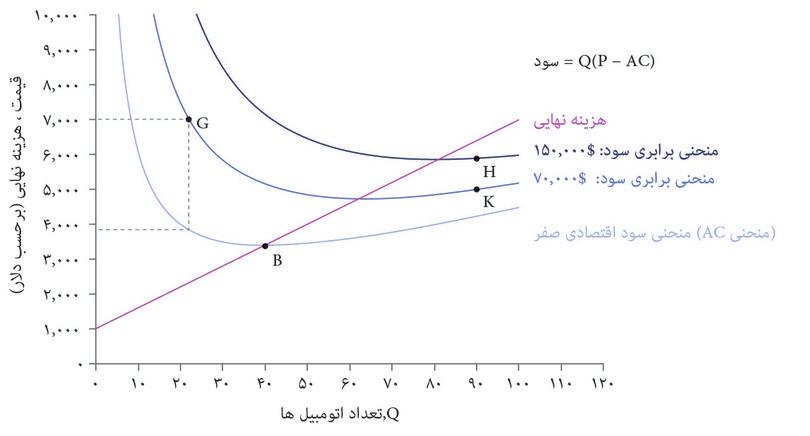
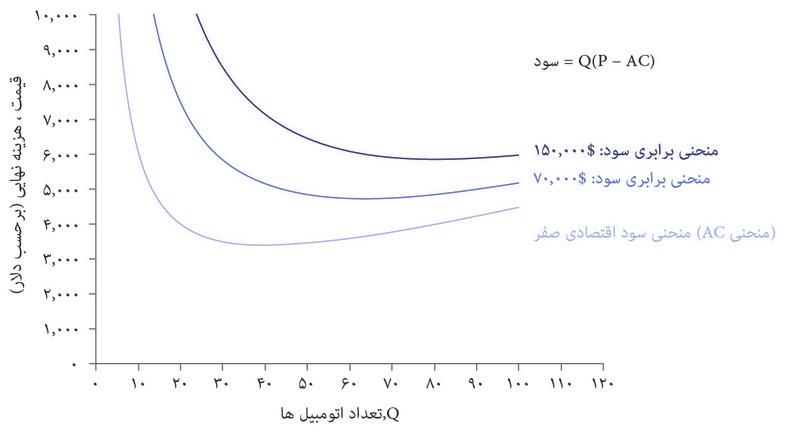
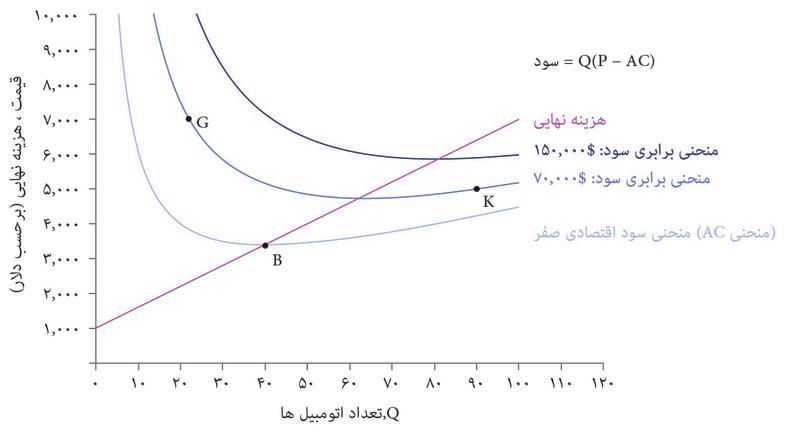
از روی این معادله میتوانید ببینید که شکل منحنیهای برابری سود بهشکل منحنی میانگین هزینه بستگی خواهد داشت. بیاد داریم که برای شرکت اتومبیلهای زیبا، منحنی میانگین هزینه تا نقطه Q = ۴۰, شیب رو به پایین و پس از آن شیب رو به بالا دارد. شکل ۷.۱۰ منحنیهای برابری سود متناظر با آن را نشان میدهد. میبینیم که مشابه منحنیهای مربوط به چیروز بهنظر میرسند اما تفاوتهایی هم وجود دارد چراکه تابع میانگین هزینه شکل متفاوتی دارد. پایینترین منحنی (کمرنگترین آبی) منحنی سود-اقتصادیِ-صفر را نشان میدهد: یعنی ترکیباتی از قیمت و تعداد که در ازای آن سود اقتصادی برابر با صفر است، چراکه قیمت دقیقاً برابر با میانگین هزینه در هر تعداد است.
توجه کنید که در شکل ۷.۱۰:
- منحنیهای برابری سود در نقاطی که در آن P > MCاست، شیب رو به پایین دارند.
- منحنیهای برابری سود در نقاطی که در آن P < MCاست، شیب رو به بالا دارند.
- حاشیه سود
- تفاوت بین قیمت و هزینه نهایی.
تفاوت میان قیمت و هزینه نهایی را سود نهاییمینامیم. در هر نقطه روی منحنی برابری سود، شیب خط عبارت است از:
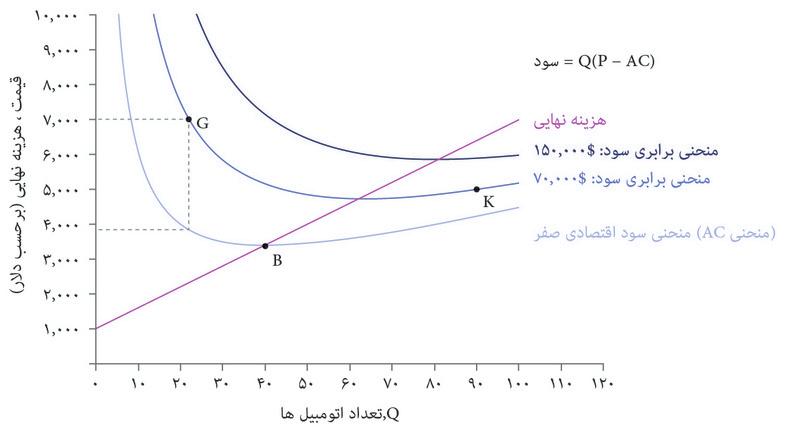
برای اینکه بفهمیم چرا، دوباره نقطه G در شکل ۷.۱۰ را بیاد بیاوریم، نقطهای که در آن Q=۲۸ است و قیمت بسیار بالاتر از هزینه نهایی است. اگر:
- تعداد یا Q را بهاندازه ۱ واحد افزایش دهیم
- و قیمت را بهاندازه (P − MC)/Qکاهش دهیم
آنگاه سود شما ثابت خواهند ماند، چرا که سود اضافی شما روی اتومبیل ۱۹ ام یعنی (P − MC) با یک کاهش درآمدی بهاندازه (P − MC) روی ۲۸ اتومبیل دیگر جبران خواهد شد.
لایبنیتز: منحنیهای برابری سود و شیب آنها
همین استدلال در مورد هر نقطه دیگری که در آن P > MCباشد نیز صدق میکند. حاشیه سود مثبت است پس شیب منفی است. و همینطور در مورد وضعیتی که P < MCاست نیز صادق است. در این مورد حاشیه سود منفی است بطوریکه برای ثابت نگه داشتن سود در شرایطی که تعداد بهاندازه 1 واحد بیشتر میشود، به یک افزایش قیمتی نیاز داریم. منحنی برابری سود شیب رو به بالا دارد.
پرسش ۷.۸ (یک پاسخ را انتخاب کنید).
نمودار زیر، منحنی هزینه نهایی (MC)، منحنی میانگین هزینه (AC)، و منحنی های برابری سودِ یک شرکت را نشان می دهد. براساس اطلاعات موجود در نمودار می توان گفت که:
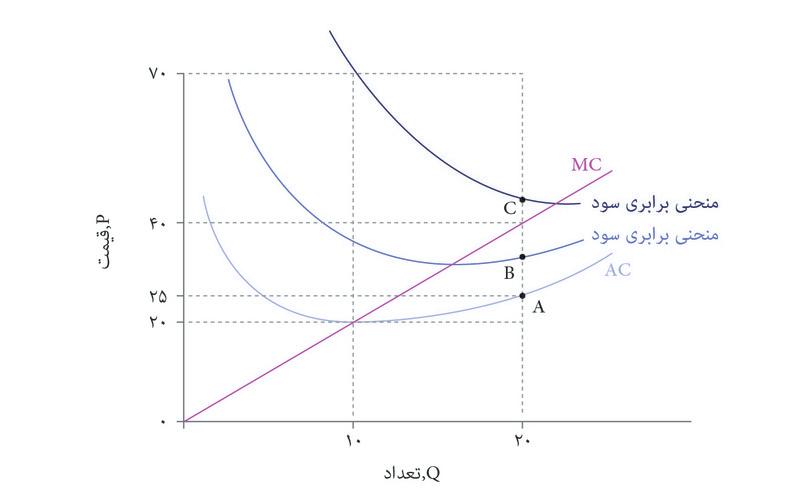
- (الف) سود در هر نقطه روی منحنی AC صفر است (زیرا قیمت با میانگین هزینه برابر است، و سود = تعداد فروخته شده × ضربدر (قیمت – میانگین هزینه)).
- (ب) سطح سود برای منحنی برابری سودی که از نقطه B می گذرد را می توان در نقطه Q = ۱۰ جایی که AC = ۲۰ و P = ۴۰است، محاسبه کرد. بنابراین سود = (۴۰ – ۲۰) ضربدر تعداد فروش × ۱۰ = ۲۰۰.
- (ج) سطح سود برای منحنی برابری سودی که از نقطه C می گذرد را می توان در نقطه Q = ۱۰یعنی جایی که AC = ۲۰، و P = ۷۰است محاسبه کرد. در نقطه C تعداد مساوی با ۲۰ است،Q = ۲۰و بنابراین سود هر واحد عبارت است از(P − AC) = ۲۵. از آنجا که AC برابر با ۲۵ است، قیمت یا P باید برابر با ۵۰ باشد.
- (د) سطح سود برای منحنی برابری سودی که از نقطه B می گذرد را می توان در نقطه ای که تعداد ۱۰ است، Q = ۱۰، یعنی جایی که AC = ۲۰ و P = ۴۰. است. بنابراین سود (۴۰ − ۲۰) × ۱۰ = ۲۰۰. در نقطه B ،Q = ۲۰, است و بنابراین سود هر واحد عبارت است از (P − AC) = ۱۰. ازآنجاکه AC برابر با ۲۵ است، قیمت یا P بایستی برابر ۳۵ باشد.
تمرین ۷.۴ چگونه منحنیهای برابری سود را نگاه کنیم؟
منحنیهای برابری سود چیروز شیب رو به پایین دارند، اما در مورد اتومبیلهای زیبا وقتی تعداد پایین باشد رو به پایین و وقتی تعداد بالا باشد رو به بالا هستند.
- در هر دو مورد، با افزایش کمیت، منحنیهای برابری سود بالاتر، به منحنی میانگین هزینه نزدیکتر میشوند. چرا؟
- دلیل تفاوت در شکل منحنی برابری بین دو بنگاه اقتصادی چیست؟
۷.۵ تعیین قیمت و تعداد برای حداکثرکردن سود
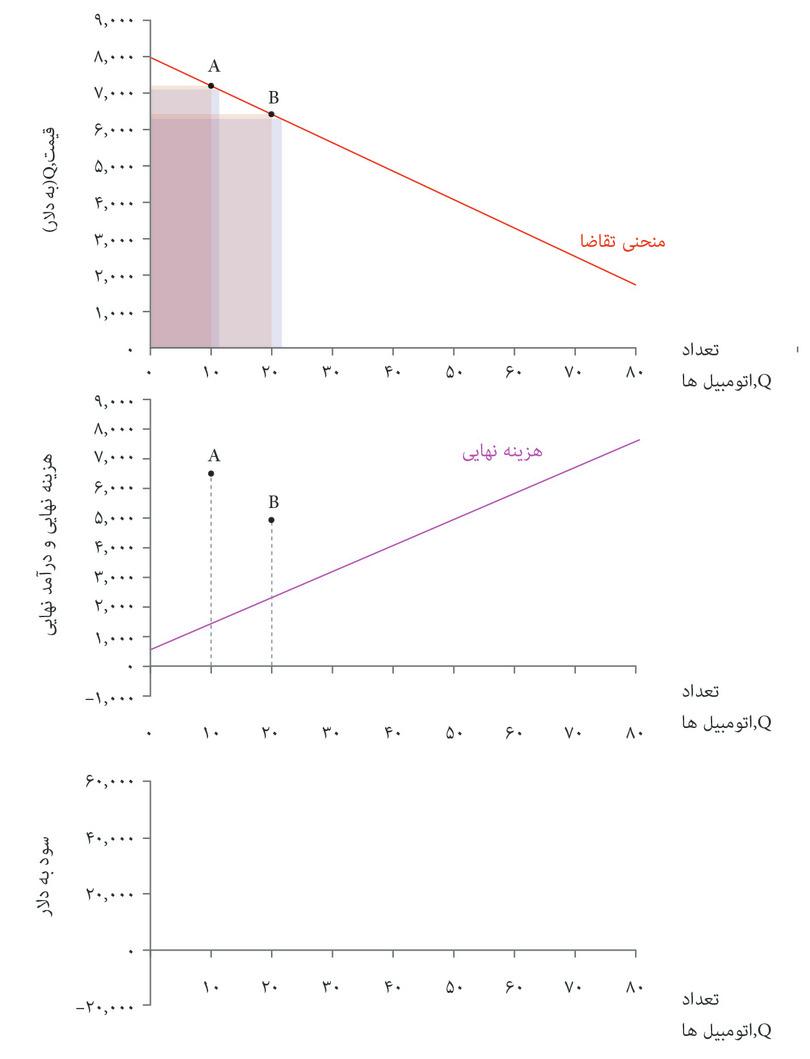
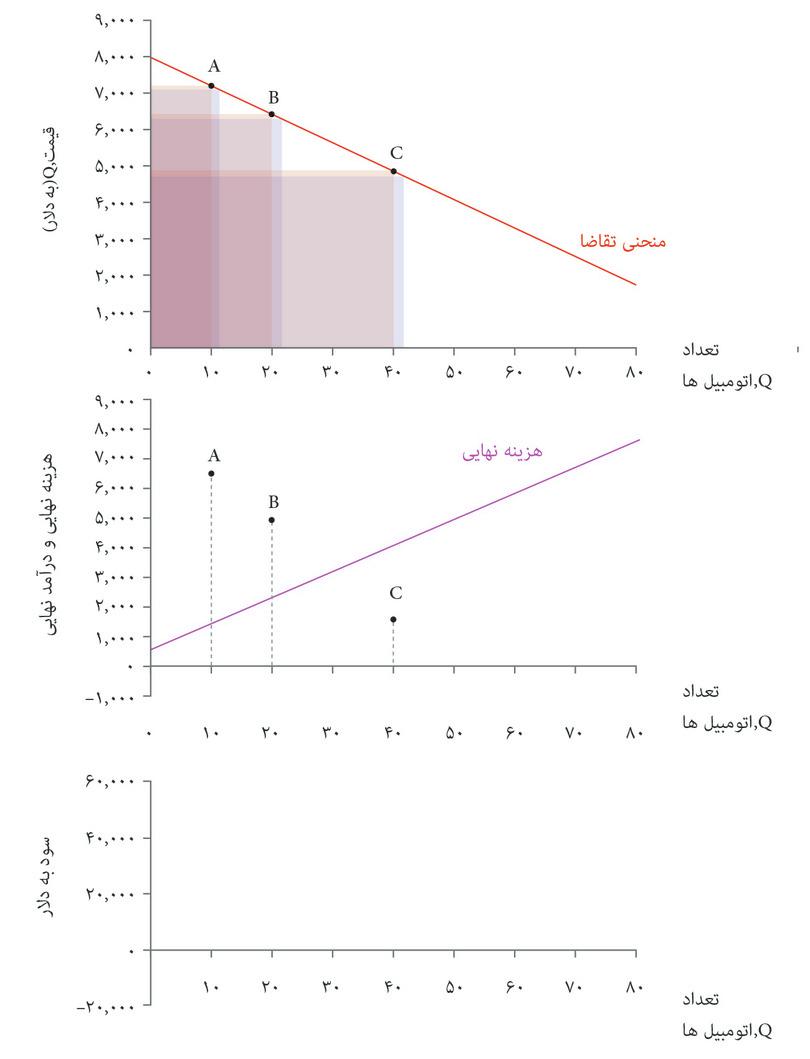
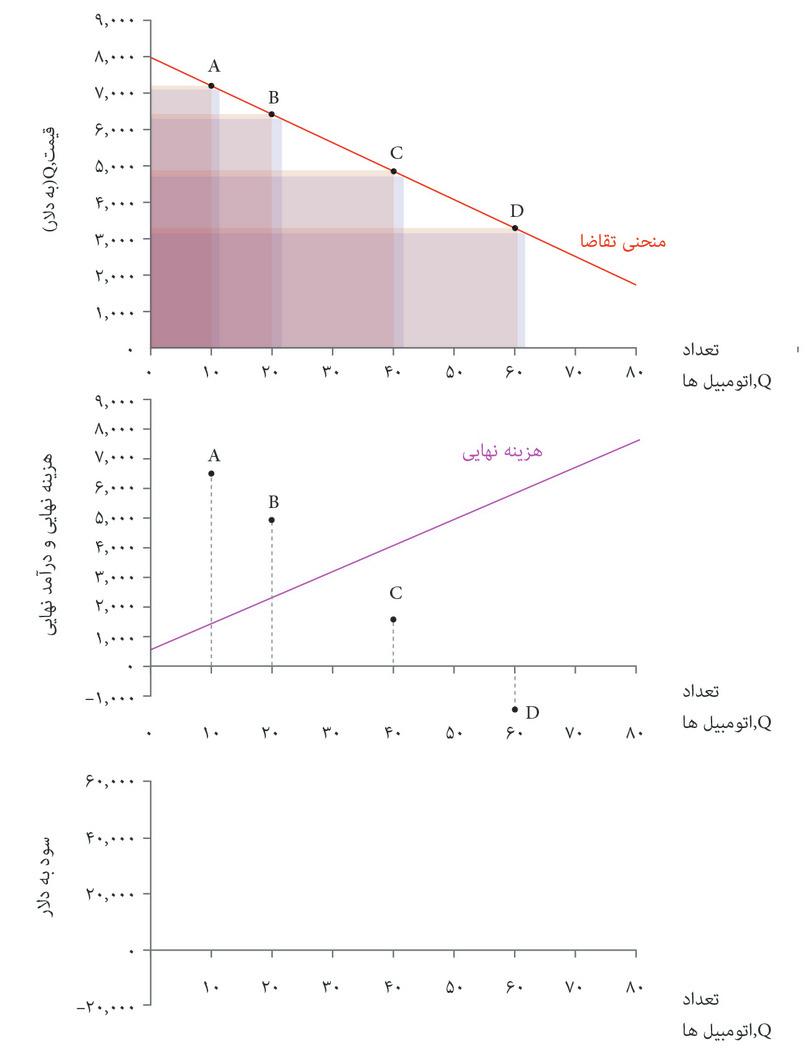
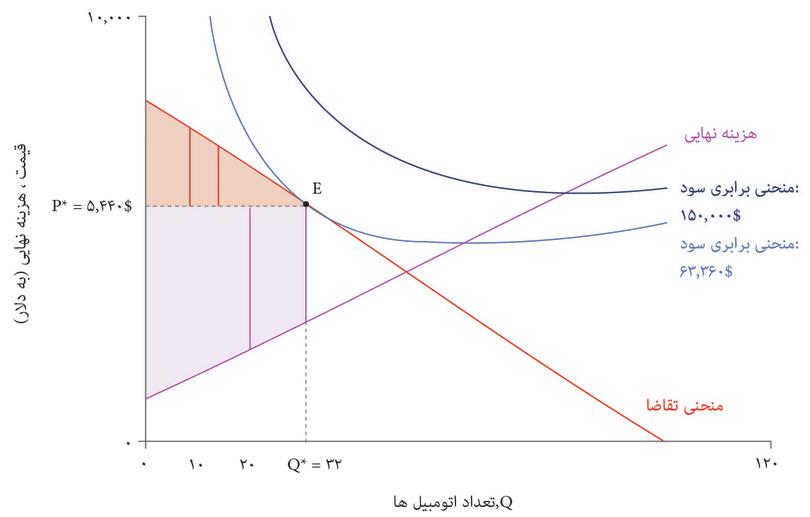
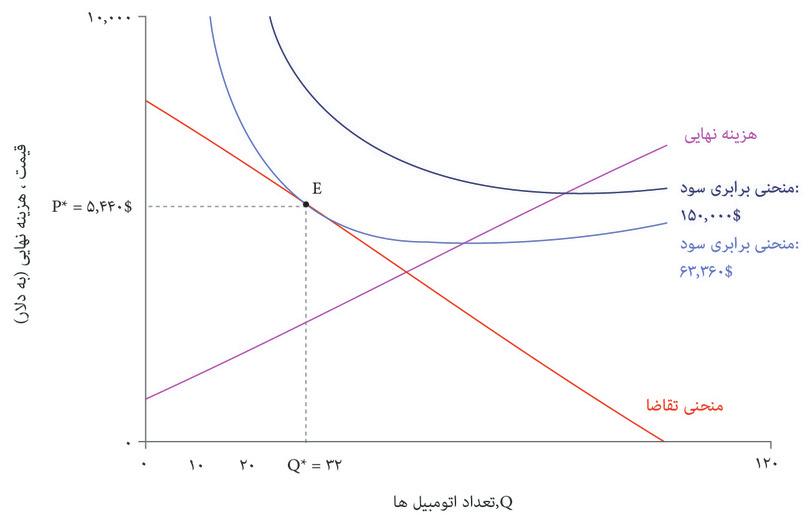
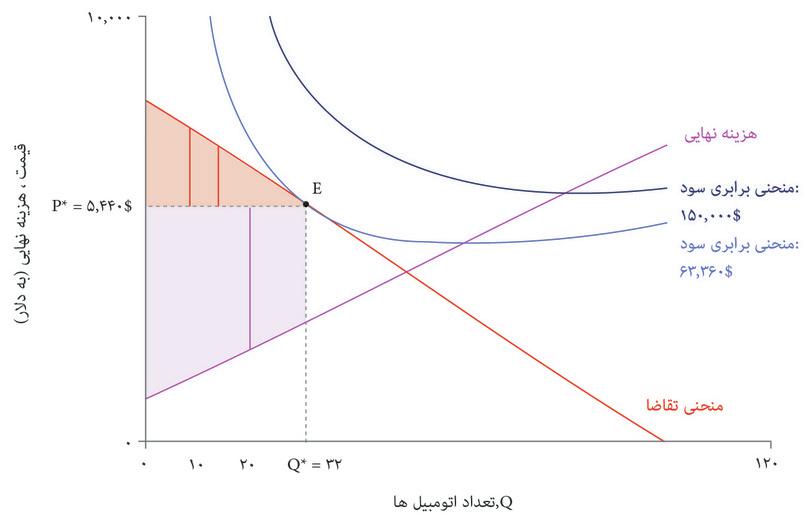
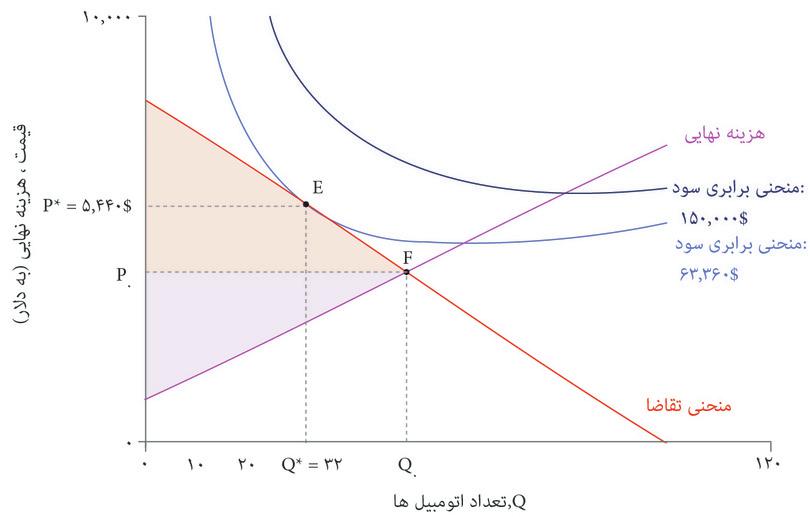
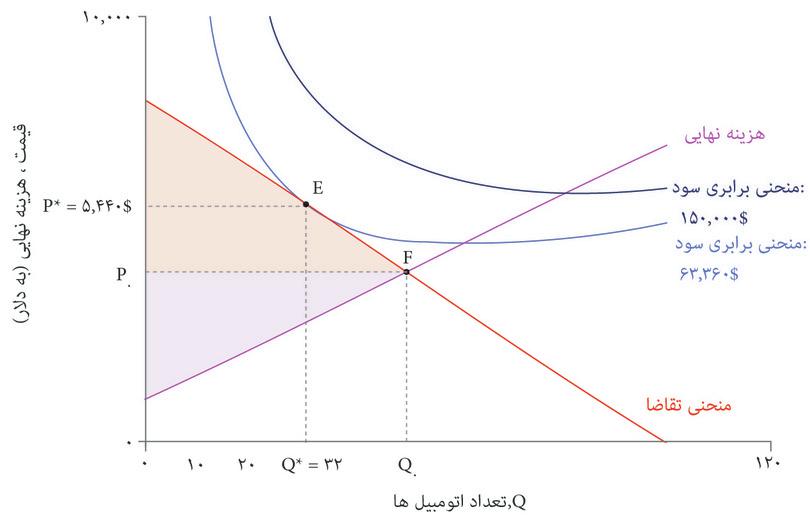
در شکل ۷.۱۱ هم منحنی تقاضا و هم منحنیهای برابری سود کمپانی اتومبیلهای زیبا را نشان دادهایم. بهترین گزینه قیمت و تعداد برای تولید کننده کدام است؟
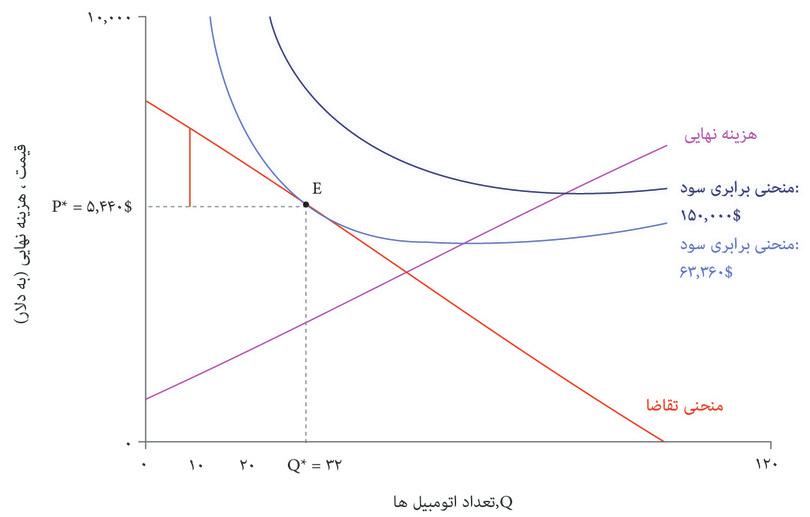
تنها انتخابهای مقرون بهصرفه نقاطی هستند که روی یا پایینتر از منحنی تقاضا قرار دارند که آن را با منطقه سایه دار روی نمودار نشان دادهایم. برای به حداکثررساندن سود، بنگاه اقتصادی باید نقطه مماس E را انتخاب کند که روی بالاترین منحنی سود ممکن قرار دارد.
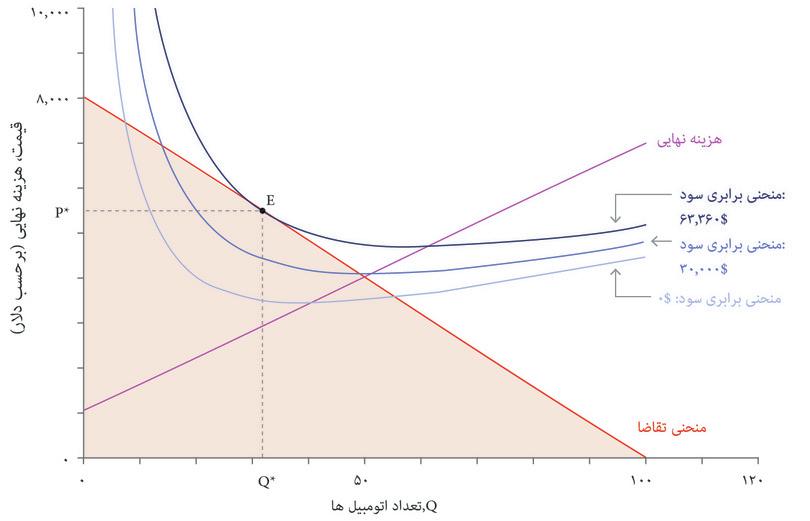
شکل ۷.۱۱ انتخاب قیمت و تعداد اتومبیلهای زیبا برای به حداکثررساندن سود.
قیمت و تعداد به حداکثررساننده سود عبارتند از P* = $۵۴۴۰ و Q* = ۳۲، و سود متناظر با آن $۶۳۳۶۰ است. در اینجا هم مثل مورد چیروز، ترکیب بهینه قیمت و تعداد، بده-بستانی را که بنگاه اقتصادی تمایل خواهد داشت میان قیمت و تعداد (بهازای یک سطح سود معلوم) برقرار کند، دربرابر بده-بستانی که منحنی تقاضا بنگاه اقتصادی را وادار و محدود به آن میکند، موازنه میکند.
در نقطه مماس سود بنگاه اقتصادی حداکثر میشود، جایی که شیب منحنی تقاضا با شیب منحنی برابری سود برابر میشود، بطوریکه دو بده-بستان در توازن قرار میگیرند:
- منحنی تقاضا همان خط مقرون بهصرفهگی است، و شیب آن، نرخ نهایی تبدیل (MRT) قیمت کمتر به تعداد فروخته شده ی بیشتر است.
- منحنی برابری سود همان منحنی بیتفاوتی است، و شیب آن، نرخ نهایی جانشینی (MRS) در ایجاد سود، میان فروش بیشتر و تعیین قیمت بیشتر است.
نقطه E، یعنی نقطه سود حداکثری، نقطهای است که در آن MRT=MRS است.
لایبنیز: قیمت به حداکثررساننده سود
اتومبیلهای زیبا، درمقایسه با غولهای چندملیتی صنعت اتومبیلسازی، بنگاه اقتصادی بسیار کوچکی محسوب میشود: میخواهد تنها ۳۲ اتومبیل در روز تولید کند. بلحاظ سطح تولید (و البته نه قیمت) بیشتر شبیه برندهای لوکسی مثل اَستون-مارتین، رولز-رویس و لامبورگینی است که هر کدامشان کمتر از ۵۰۰۰ اتومبیل در سال تولید میکنند. اندازه اتومبیلهای زیبا را تا حدی تابع تقاضای آن تعیین میکند – با هر قیمت، تنها ۱۰۰ خریدار بالقوه در روز وجود دارد. در درازمدت بنگاه اقتصادی میتواند تقاضا را بواسطه تبلیغات افزایش دهد: زیرا محصول را در میدان توجه مصرفکنندگان بیشتری قرار میدهد و آنها را نسبت به کیفیات مطلوب آن متقاعد میکند. اما اگر میخواهد تولید را گسترش دهد، باید به ساختار هزینههای خود نگاه کند. مانند شکل ۷.۷در حال حاضر، هزینههای نهایی بهسرعت بالاروندهای را نشان میدهد، بطوریکه میانگین هزینه بهمحض اینکه خروجی از ۴۰ بیشتر میشود، بالاتر میرود. برای بنگاه اقتصادی مشکل است که با تأسیسات و تجهیزات فعلی خود بیشتر از ۴۰ تولید کند. سرمایه گذاری در تجهیزات جدید ممکن است به کاهش هزینههای نهایی آن کمک کند و گسترش را ممکن کند.
بهینهسازی محدود
- مسأله انتخاب محدود
- این مسأله درباره این است که چگونه میتوانیم، با توجه به ترجیحات و محدودیتهایمان و وقتی که کالایی که برای آن ارزش قائل هستیم کمیاب است، بهترین اقدام را برای خود انجام دهیم. همچنین نکاه کنید به: مشکل بهینهسازی محدود
مسأله به حداکثررسانی سود نیز نمونه دیگری از مسائل انتخاب محدود است، مثل نمونههایی که در فصلهای قبل دیدیم: مثل انتخاب زمان مطالعه الکسی، انتخاب شما یا آنجلا در مورد ساعات کار و انتخاب دستمزد توسط کارفرمای ماریا.
هر کدام از این مسائل ساختار واحدی دارند:
- تصمیم-ساز تلاش دارد تا ارزشهای یک یا چند متغیر را بهمنظور دستیابی به یک هدف تعیین کند. در مورد اتومبیلهای زیبا، متغیرها عبارتند از قیمت و تعداد.
- هدف بهینهسازی چیزی است: به حداکثررساندن مطلوبیت، حداقلسازی هزینهها و یا حداکثرسازی سود. تصمیم-ساز با یک *مانع محدودکننده مواجه میشود، که دامنه مقرون بهصرفهگی را محدود میکند: از تابع تولید آنجلا، تا محدودیت بودجه ای، منحنی بهترین پاسخ ماریا یا منحنی تقاضا برای اتومبیلهای زیبا.
در هر مورد، ما انتخاب تصمیم-ساز را بهشکل تصویری، و با استفاده از منحنیهای بیتفاوتی که به هدف مربوط میشوند (برابری-مطلوبیت، برابری هزینه، یا برابری سود) و مجموعه مقرون بهصرفه خروجیها که بواسطه مانع یا حد تعیین میشوند، نشان دادهایم. و راهحل مسأله را در نقطه مماس پیدا کردهایم، نقطهای که در آن MRS (یا شیب منحنی بیتفاوتی) با MRT (شیب خط مانع) برابر است.
بهینهسازی محدود
،تصمیم-ساز، ارزش یک یا چند متغیر را تعیین میکند
- … در جهت دستیابی به یک هدف
- … و براساس محدودیت یا مانعی که مجموعه مقرون بهصرفهگی را معین میکند
بهینهسازی محدود کاربردهای بسیاری در علم اقتصاد دارد؛ چنین مسائلی را می توان هم بهشکل ریاضی و هم بهشکل تصویری حل کرد.
پرسش ۷.۹ (یک پاسخ را انتخاب کنید).
شکل ۷.۱۱ منحنی تقاضای اتومبیلهای زیبا را همراه با منحنی های هزینه نهایی و برابری سود نشان می دهد. ترکیب تعداد-قیمت در نقطه E عبارت است از (Q*, P*) = (۳۲، ۵، ۴۴۰).میانگین هزینه تولید ۵۰ اتومبیل با میانگین هزینه تولید ۳۲ اتومبیل یکسان است. فرض کنید که بنگاه اقتصادی قیمت را در P = $۵.۴۴۰ ثابت نگه می دارد اما حالا بجای ۳۲ اتومبیل ۵۰ اتومبیل تولید می کند. کدامیک از گزینه های زیر صحیح است؟
- (الف) از روی منحنی تقاضا میتوانیم بفهمیم که با قیمت ۵۴۴۰ دلار بنگاه اقتصادی تنها میتواند ۳۲ اتومبیل بفروشد.
- (ب) سود بنگاه اقتصادی بواسطه هزینه تولید ۱۸ اتومبیل اضافی که حالا فروش نرفته باقی ماندهاند، کاهش یافته است.
- (ج) سود بنگاه اقتصادی بواسطه هزینه تولید ۱۸ اتومبیل اضافی که حالا فروش نرفته باقی ماندهاند، کاهش یافته است.
- (د) سود بنگاه اقتصادی بواسطه هزینه تولید ۱۸ اتومبیل اضافی که حالا فروش نرفته باقی ماندهاند، کاهش یافته است.
پرسش ۷.۱۰ (یک پاسخ را انتخاب کنید).
شکل ۷.۱۱ منحنی تقاضای اتومبیل های زیبا را همراه با منحنی های هزینه نهایی و برابری سود نشان می دهد. در نقطه E ترکیب تعداد-قیمت عبارت است از (Q*, P*) = (۳۲،۵و۵.۴۴۰,) و سود برابر است با ۶۳۶۳۰ دلار.
فرض کنید که حالا بنگاه اقتصادی تصمیم می گیرد تعداد Q = ۳۲ اتومبیل تولید کند و قیمت را P = $۵و۴۰۰. دلار بگذارد. کدامیک از گزینه های زیر صحیح است؟
- (الف) ازآنجاکه تعداد همچنان ۳۲ است، هزینه تولید یکسان باقی می ماند، اما عایدی افت می کند و بنابراین سود کاهش پیدا می کند.
- (ب) ازآنجاکه تعداد همچنان ۳۲ است، هزینه تولید یکسان باقی می ماند، اما عواید به اندازه ۴۰ دلار در هر اتومبیل و بنابراین ۱۲۸۰ دلار بطورکل افت می کند. بنابراین سود عبارت خواهد بود از: $۶۳.۳۶۰ – $۱.۲۸۰ = $۶۲.۰۸۰.
- (ج) در نقطه E، یعنی جایی که تعداد ۳۲ و قیمت ۵۴۴۰ دلار است، سود برابر با ۶۳۳۶۰ دلار خواهد بود. بنابراین سود به ازای هر اتومبیل عبارت ۵۴۴۰ – AC = $۱۹۸۰ ، AC باید ۳۴۶۰ دلار باشد. صرفنظر از قیمتی که تعیین می شود AC همواره یکسان است.
- (د) با قیمت پائین تر تقاضای بازار بیشتر از ۳۲ است و بنابراین بنگاه اقتصادی میتواند همه ۳۲ اتومبیل را با قیمت جدید به فروش برساند.
پرسش ۷.۱۱ (یک پاسخ را انتخاب کنید)
شکل ۷.۱۱ منحنی تقاضا برای اتومبیل های زیبا را به همراه منحنی های هزینه نهایی و برابری سود نشان می دهد.
فرض کنید که بنگاه اقتصادی تصمیم می گیرد از قیمت P^ = $۵۴۴۰ و تعداد Q^ = ۳۲ به قیمت بالاتری برود و یا قیمت جدید سطح خروجی ای را در نظر می گیرد که بالاترین سطح سود را داشته باشد. کدامیک از گزاره های زیر صحیح است؟
- در قیمت های بالاتر از P^ ، حداکثر تعداد اتومبیلهای قابل فروش کمتر از ۳۲ است و بنگاه اقتصادی بیشتر از تعدادی که می تواند بفروشد تولید نخواهد کرد.
- بنگاه اقتصادی کمتر از ۳۲ اتومبیل تولید خواهد کرد. منحنی هزینه نهایی شیب افزایشی دارد، بطوری که با خروجی کمتر هزینه نهایی هم کمتر می شود.
- بنگاه اقتصادی کمتر از ۳۲ اتومبیل تولید خواهد کرد، بنابراین هزینه های کل آن کمتر خواهد بود.
- هر نقطه مقرون به صرفه ای غیر از E روی منحنی برابری سودِ پائین تری قرار خواهد داشت.
۷.۶ نگرش دیگری به حداکثرسازی سود: درآمدهای نهایی و هزینههای نهایی
در بخش قبلی نشان دادیم که نقطه حداکثرسازی سود برای اتومبیلهای زیبا نقطهای بود که در آن منحنی تقاضا بر منحنی برابری سود مماس میشود. برای به حداکثررساندن سود، باید ۳۲ اتومبیل تولید کند و با قیمت ۵۴۰۰ دلار بفروشد.
- عواید نهایی
- افزایش در عواید ناشی از افزایش تعداد از Q به Q+۱.
حالا روش دیگری برای پیداکردن نقطه حداکثرسازی سود را بررسی میکنیم که نیازی به استفاده از منحنیهای برابری سود ندارد. بجای آن از منحنی درآمد نهایی استفاده میکنیم. بیاد داشته باشید که اگر Q تعداد اتومبیل با قیمت Pفروخته شوند، آنگاه درآمد یا R عبارت خواهد بود از R = P × Q. درآمد نهایییا MR، افزایشی در درآمد است که از محل افزایش تعداد از Q به Q + ۱ ناشی میشود.
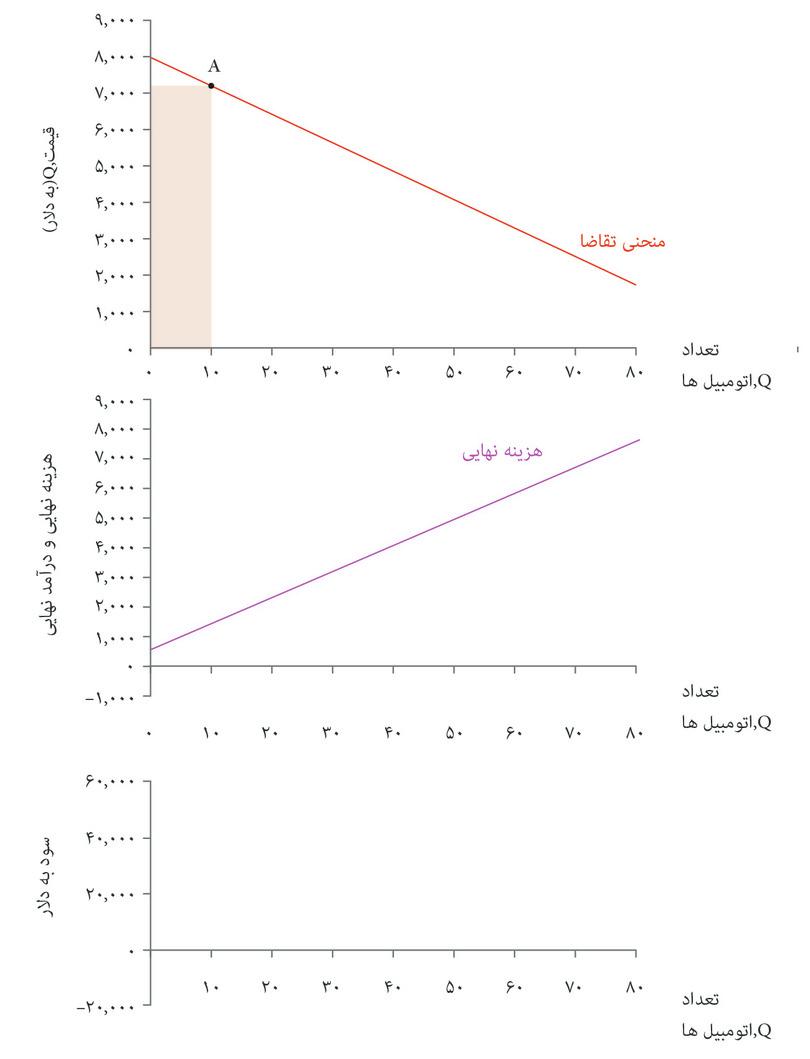
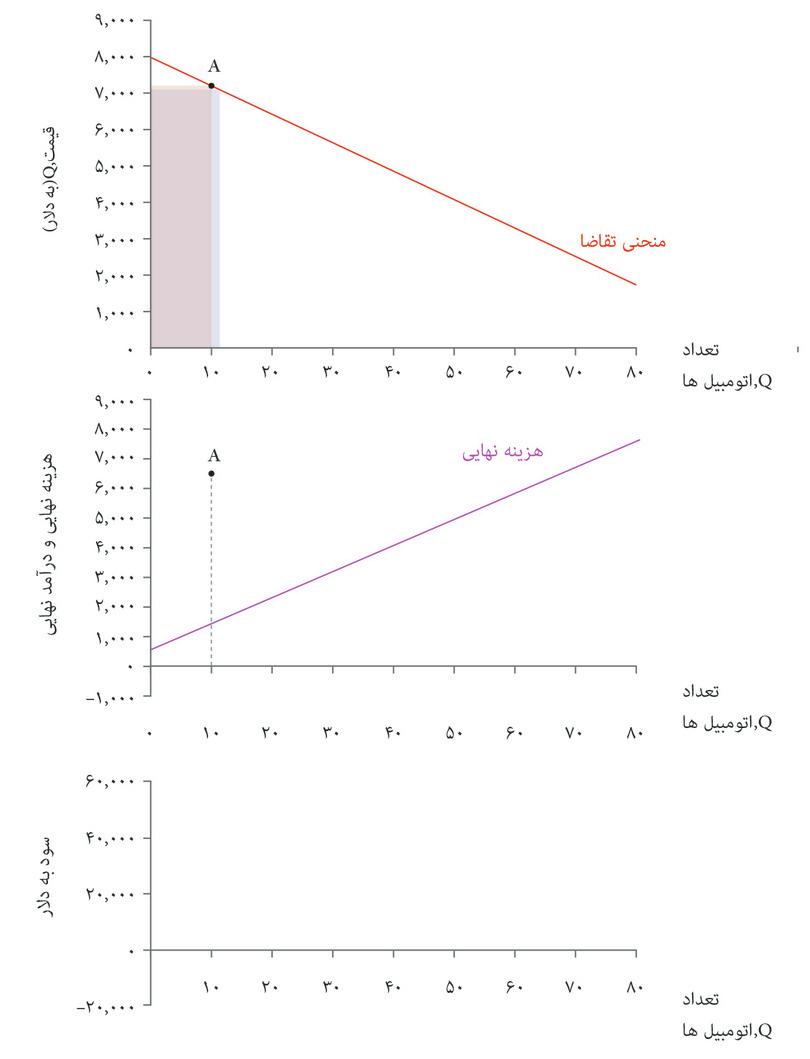
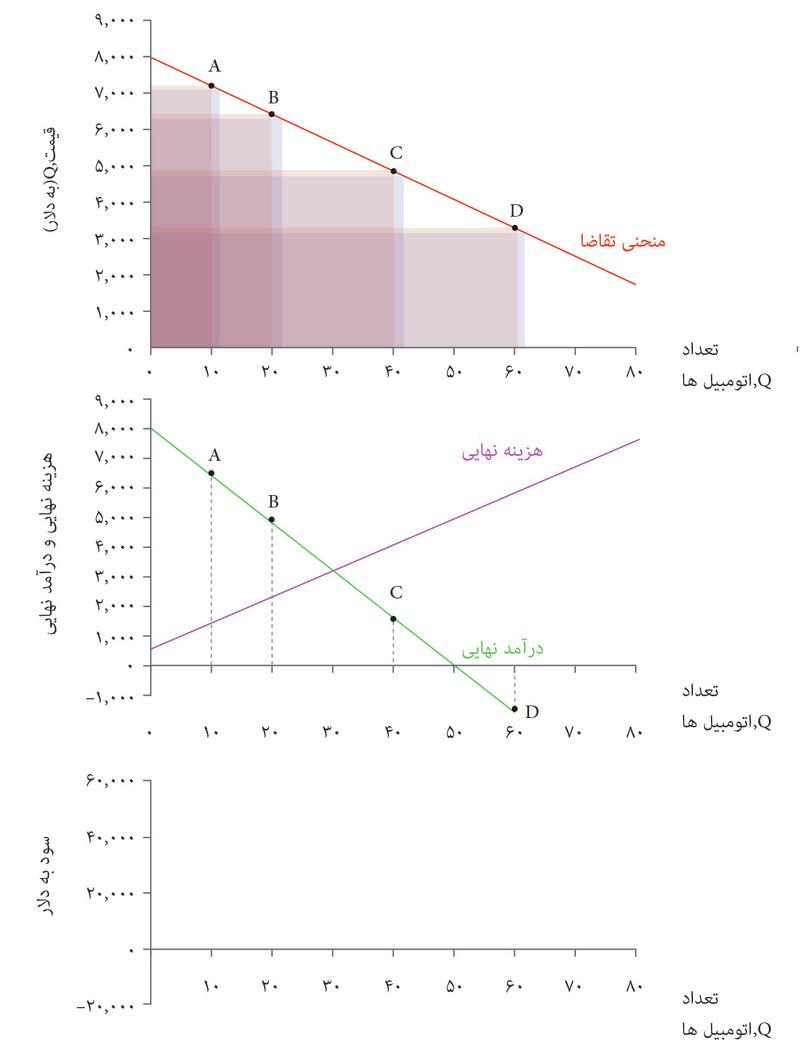
شکل ۷.۱۲ الف به شما نشان میدهد که چگونه وقتی Q = ۲۰است، درآمد نهایی، یعنی درآمد ناشی از افزایش تعداد به اندازه یک واحد، را محاسبه کنید.
شکل ۷.۱۲ الف نشان میدهد که درآمد بنگاه اقتصادی عبارت است مساحت مستطیلی که زیر منحنی تقاضا رسم شده است. وقتی تعداد را از ۲۰ به ۲۱ افزایش میدهیم، به دو دلیل درآمد تغییر میکند: یک اتومبیل اضافی با قیمت جدید فروخته میشود، اما ازآنجا که قیمت جدید برای تعداد ۲۱ کمتر است، بنابراین یک کسری ۸۰ دلاری بهازای هر یک از بقیه ۲۰ ماشین دیگر هم وجود دارد. درآمد نهایی، نتیجه نهایی این دو تغییر است.
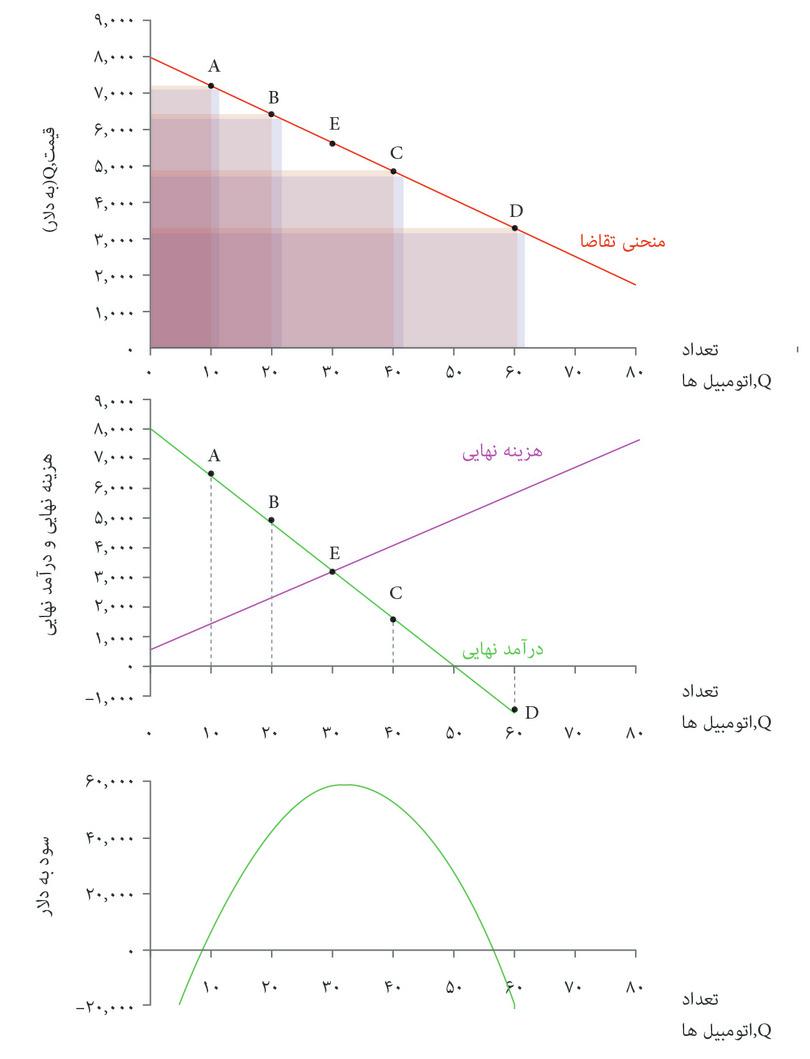
در شکل ۷.۱۲ ب، منحنی درآمد نهایی را پیدا میکنیم و از آن برای پیدا کردن نقطه سود حداکثری استفاده میکنیم. قاب بالایی منحنی تقاضا را نشان میدهد و قاب وسطی منحنی هزینه نهایی را. خطوط کناره نشان میدهند که چگونه باید منحنی درآمد نهایی را محاسبه و رسم کنید. وقتی قیمت بالا و تعداد کم است، MR بالا است: یعنی آورده حاصل از فروش یک اتومبیل بیشتر، بسیار بزرگتر از کل کسری ناشی از تعداد کمی از اتومبیلهای دیگر. هرچه به پایین منحنی تقاضا نزدیک میشویم قیمت کمتر میشود (و بنابراین آورده ناشی از اتومبیل آخری کوچکتر میشود) و تعداد افزایش پیدا میکند (و بنابراین کل کسری ناشی از اتومبیلهای دیگر بزرگتر است) و بنابراین MR کاهش پیدا میکند تا به یکباره منفی میشود.
منحنی درآمد نهایی عموماً (و اگرچه نه ضرورتاً) یک خط با شیب کاهشی است. دو قاب پایینی شکل ۷.۱۲ب نشان میدهد که نقطه سود حداکثری جایی است که منحنی MR منحنی MC را قطع میکند. برای اینکه بدانیم چرا بیاد بیاوریم که سود تفاوت میان درآمد و هزینه است، و بنابراین در ازای هر ارزشی از تعداد، تغییر در سود ناشی از افزایش تعداد بهاندازه یک واحد (سود نهایی)، عبارت خواهد بود از تفاوت میان تغییر در درآمد و تغییر در هزینهها:
بنابراین:
- اگر MR > MC باشد، بنگاه اقتصادی میتواند با افزایش تعداد، سود را بالاتر ببرد.
- و اگر MR < MC باشد، سودِ نهایی منفی است. کاهشِ تعداد اقدام بهتری خواهد بود.
لایبنیتز: درآمد نهایی و هزینه نهایی
در پایینترین قاب شکل ۷.۱۲ب ملاحظه میکنید که چگونه سود همراه با تعداد تغییر میکند. همانطور که هزینه نهایی شیب تابع هزینه است، سود نهایی هم شیب تابع سود است. در این مورد:
- وقتی Q < ۳۲ باشد، MR > MC است: سود نهایی مثبت است، بنابراین سود همراه با تعداد افزایش پیدا میکند.
- وقتی Q > ۳۲ باشد، MR < MC است: سود نهایی منفی است، سود همراه با تعداد کاهش پیدا میکند.
- وقتی Q = ۳۲ باشد، MR = MC است: سود به حداکثر میرسد.
پرسش ۷.۱۲ (یک پاسخ را انتخاب کنید).
این شکل منحنیهای هزینه نهایی و درآمد نهایی شرکت اتومبیلهای زیبا را نشان میدهد. براساس اطلاعات موجود، کدامیک از گزارههای زیر صحیح است؟
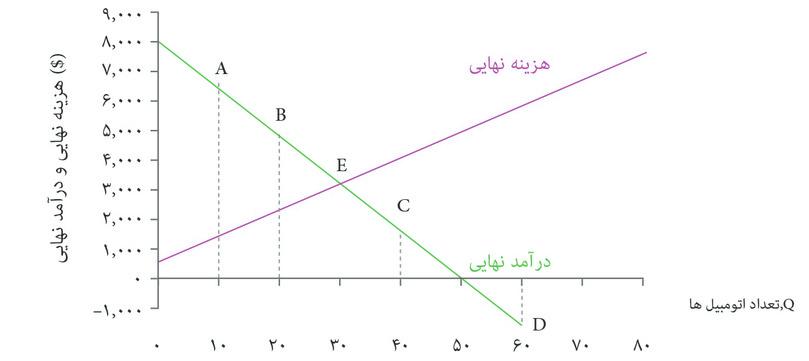
- (الف) وقتی تعداد ۴۰ است، هزینه نهایی بزرگتر از درآمد نهایی است و بنابراین درآمد نهایی منفی است. این بدان معنا نیست که سود منفی است.
- (ب) در حالتی که تعداد ۱۰ است، درآمد نهایی نسبت به زمانی که تعداد ۲۰ است، بزرگتر است. اما از آنجا که با افزایش خروجی از ۱۰ به ۲۰ درآمد نهایی مثبت است، میتوانیم بگوییم که درآمد در حال افزایش است: یعنی در نقطه تعدادِ ۲۰، بیشتر است.
- (ج) در نقطه E سود نهایی صفر است. اما این نقطه به حداکثر رسیدن سود است و بنابراین شرکت آن را انتخاب خواهد کرد.
- (د) در همه سطوحِ خروجی تا نقطه E، درآمد نهایی از هزینه نهایی بزرگتر است. پس با افزایش خروجی سود هم افزایش خواهد یافت – یعنی در نقطه تعداد ۲۰ بیشتر از نقطه تعداد ۱۰ خواهد بود.
۷.۷ عواید ناشی از معامله
- بهره اقتصادی
- هرگونه پرداخت یا سایر مزایایی که فرد بالاتر و علاوه بر آنچه در بهترین گزینه بعدی خود (یا گزینه ذخیره خود) بدست میآورد، بدست آورده باشد. همچنین نگاه کنید به: گزینه ذخیره
- عایدی حاصل از مبادله
- مزایایی که هر طرف، از یک تراکنش، درمقایسه با وضعیتی که هردوی آنها بدونِ مبادله بمانند، بدست میآورد. همچنین تحت عنوانِ عواید ناشی از مبادله شناخته میشود. همچنین نگاه کنید به: بهره اقتصادی.
- کارائی پارتوئی
- تخصیصی برخوردار از این ویژگی که دیگر هیچ تخصیص به لحاظ فنی مقرون به صرفه دیگری وجود ندارد که در آن یک نفر رفاه بیشتری پیدا کند بیآنکه از رفاه دیگران کاسته شود.
از فصل ۵ بیاد داریم که وقتی افراد بصورت داوطلبانه در یک تعامل اقتصادی شرکت میکنند، بهاین دلیل است که اینکار آنها را مرفهتر میکند: میتوانند مازادی بدست بیاورند که آن را بهره اقتصادیهم مینامیم. کل مازاد برای طرفین درگیر در تعامل، سنجهای برای عواید ناشی از مبادله یا عواید ناشی از تجارت است. نتایج حاصل از تعاملات میان مصرف کننده و بنگاههای اقتصادی را میتوانیم درست مثل مورد آنجلا و برونو در فصل ۵ محاسبه کنیم. قضاوت ما درباره کل مازاد، و شیوه تقسیم آن، در قالب مقولات کارایی پارتویی و عدالت (یا منصفانه بودن) است.
ما فرض کردیم که قوانین بازی برای تخصیص چیروز و اتومبیل به مصرفکنندگان، از این قرار است:
-
بنگاه اقتصادی تصمیم میگیرد که چه تعداد اقلام تولید کند، و همچنین قیمتی تعیین میکند.
-
سپس افراد مصرف کننده در مورد خرید تصمیم میگیرند.
این قوانینی انعکاسی از نهادهای بازار برای تخصیص کالاهای مصرفی است، اگرچه ممکن است راههای جایگزینی هم قابل تصور باشد – مثلاً ممکن است گروهی از افراد که به اتومبیل نیاز دارند بتوانند دور هم جمع شوند و تخصیصی را تولید کنند و سپس تولیدکنندگانی را برای مناقصه قرارداد دعوت کنند.
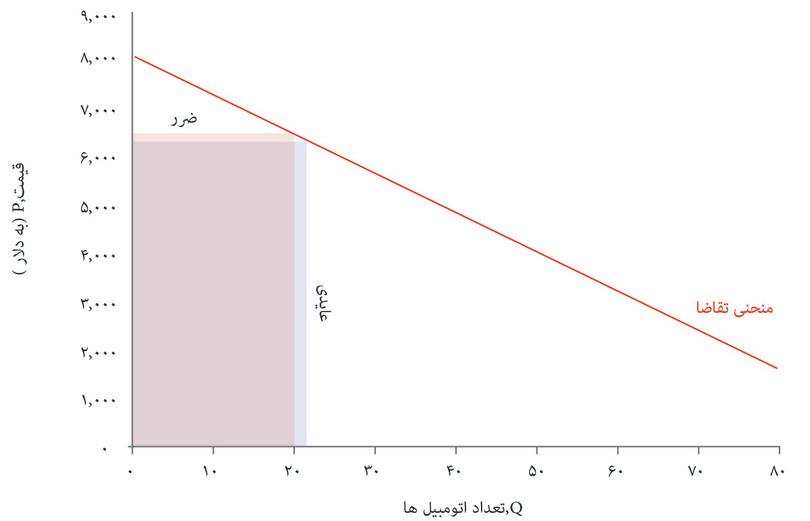
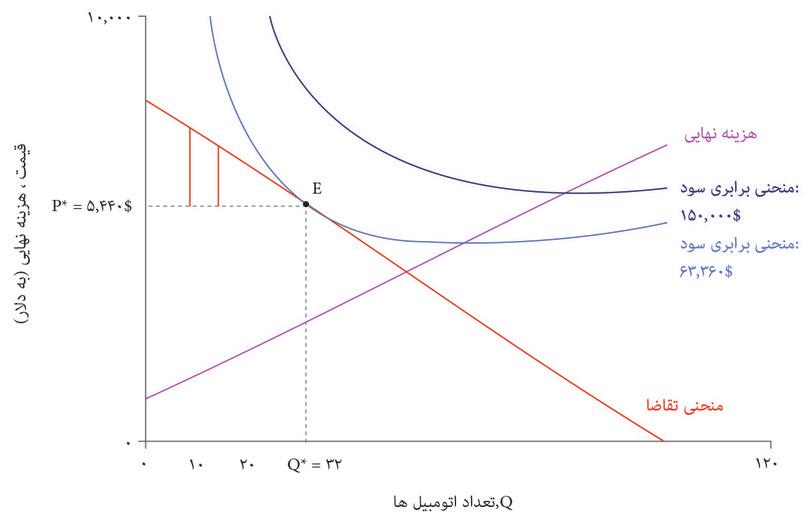
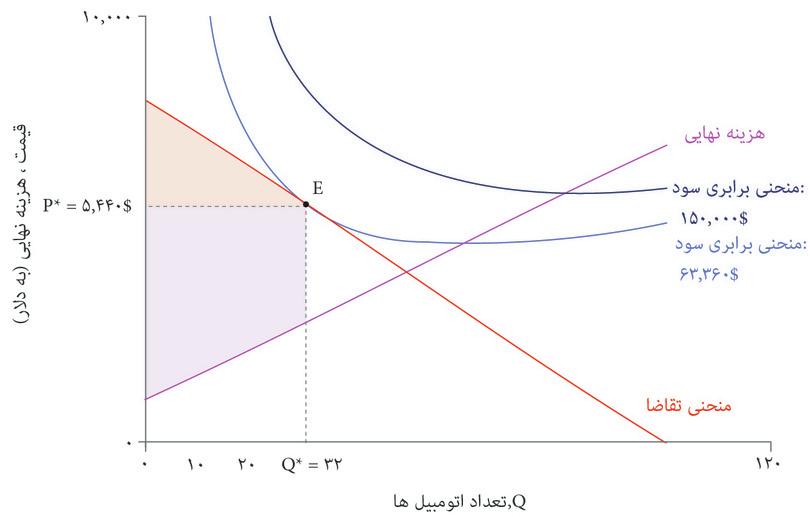
در تعاملاتی ازقبیل تعامل شرکتی مثل اتومبیلهای زیبا با مصرفکنندگان خود، مادامی که بنگاه اقتصادی قادر باشد اتومبیلی را با هزینهای کمتر از ارزش اتومبیل نزد مصرف کننده تولید کند، برای هر دو طرف عواید بالقوه وجود دارد. بیاد بیاورید که منحنی تقاضا تمایل به پرداخت (WTP) هر مصرف کننده ی بالقوه را نشان میدهد. مصرف کنندهای که تمایل به پرداخت او بالاتر از قیمت است، کالا را خریداری و مازادی دریافت میکند، زیرا ارزش اتومبیل برای او بیش از مبلغی است که باید برای آن بپردازد.
به همین ترتیب منحنی هزینه نهایی هم نشان میدهد که تولید یک اتومبیل اضافی چه هزینهای در پی دارد (از تعداد صفر که شروع کنید، منحنی هزینه نهایی نشان میدهد که تولید اولین ماشین اضافی چقدر هزینه خواهد داشت، سپس دومین ماشین اضافی و الی آخر). و اگر هزینه نهایی کمتر از قیمت باشد، بنگاه اقتصادی هم مازادی دریافت میکند. شکل ۷.۱۳ نشان میدهد که وقتی اتومبیلهای زیبا قیمت را با هدف حداکثرسازی سود انتخاب میکند، کل مازاد برای بنگاه اقتصادی و مصرفکنندگان را چگونه باید محاسبه کرد.
- مازاد مصرفکننده
- مازاد مصرفکننده: تمایلِ مصرفکننده به پرداخت برای یک کالا، منهای قیمتی که براساس آن مصرفکننده کالا را خریده است، به ازای کل واحدهای فروختهشده.
مازاد مصرف کننده، مازاد تولیدکننده، سود
- مازاد مصرف کننده، سنجهای است برای سود ناشی از مشارکت در بازار برای مصرف کننده.
- مازاد تولیدکننده پیوند نزدیکی با سود بنگاه اقتصادی دارد، اما دقیقاً با آن یکسان نیست. مازاد تولیدکننده عبارت است از تفاوت میان عواید و هزینههای نهایی بنگاه اقتصادی بهازای هر واحد، بدون احتساب هزینههای ثابت که حتی در تعداد صفر هم بر دوش بنگاه اقتصادی قرار دارند.
- سود عبارت است از مازاد تولیدکننده منهای هزینههای ثابت.
- مازاد کل ناشی از معامله در این بازار، برای بنگاه اقتصادی و برای مصرف کننده، عبارت است از مجموع مازاد مصرف کننده و شرکت کننده.
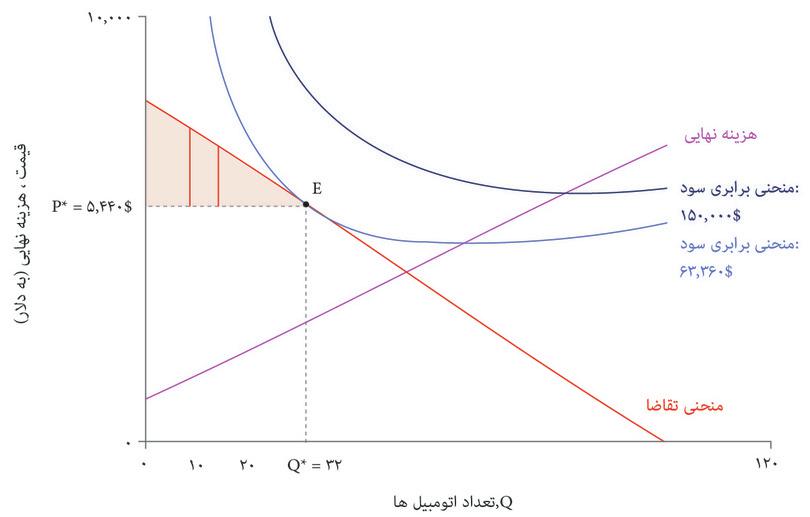
در شکل ۷.۱۳ منطقه سایه دار بالای نقطه P* مازاد مصرف کننده را میسنجد، و منطقه سایه دار زیر نقطه P* مازاد تولیدکنندهرا. از مقایسه اندازه این دو منطقه در شکل ۷.۱۳ میفهمیم که در این بازار، سهم مازاد بیشتری نصیب بنگاه اقتصادی میشود.
اینجا نیز مثل قراردادهای داوطلبانه میان آنجلاو برونو، هر دوی طرفین در بازار اتومبیلهای زیبا عایدی دارند، و تقسیم عواید تابع قدرت چانهزنی است. در این مورد، بنگاه اقتصادی قدرت بیشتری نسبت به مصرف کننده دارد زیرا تنها فروشنده اتومبیلهای زیبا بهشمار میرود. میتواند با علم به اینکه مصرفکنندگانی که این اتومبیل برایشان ارزش بالایی دارد گزینهای جز پذیرش نخواهند داشت، قیمت بالایی بگذارد و سهم بالایی از عواید را تصاحب کند. یک مصرف کننده واحد هیچ قدرتی برای چانهزنی و رسیدن به یک معامله بهتر ندارد، چراکه شرکت مشتریان بالقوه دیگری جز او دارد.
کارایی پارتویی
- کارائی پارتوئی
- تخصیصی برخوردار از این ویژگی که دیگر هیچ تخصیص به لحاظ فنی مقرون به صرفه دیگری وجود ندارد که در آن یک نفر رفاه بیشتری پیدا کند بیآنکه از رفاه دیگران کاسته شود.
- پیشرفت پارتوئی
- تغییری که بتواند دست کم به یک نفر بدون متضرر شدن بقیه نفع برساند. همچنین نگاه کنید به برتری پارتوئی.
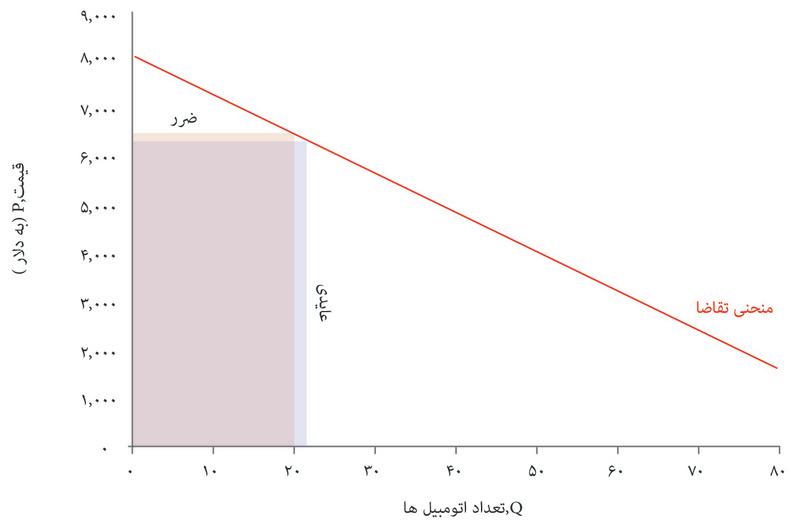
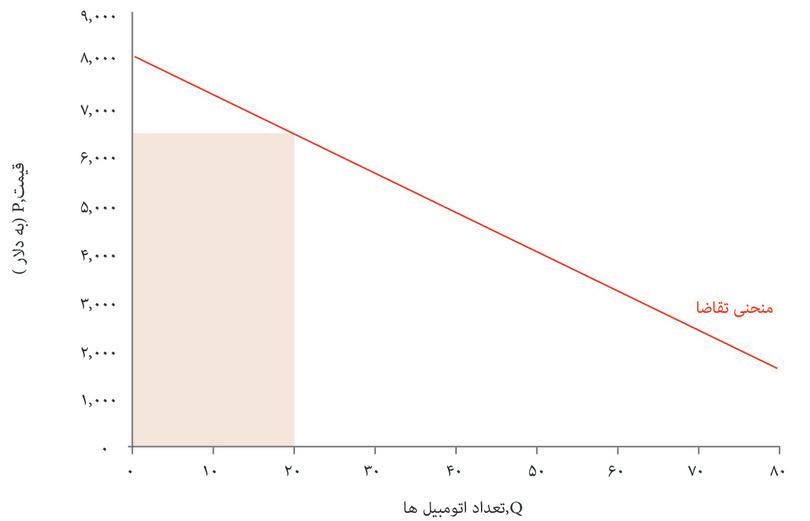
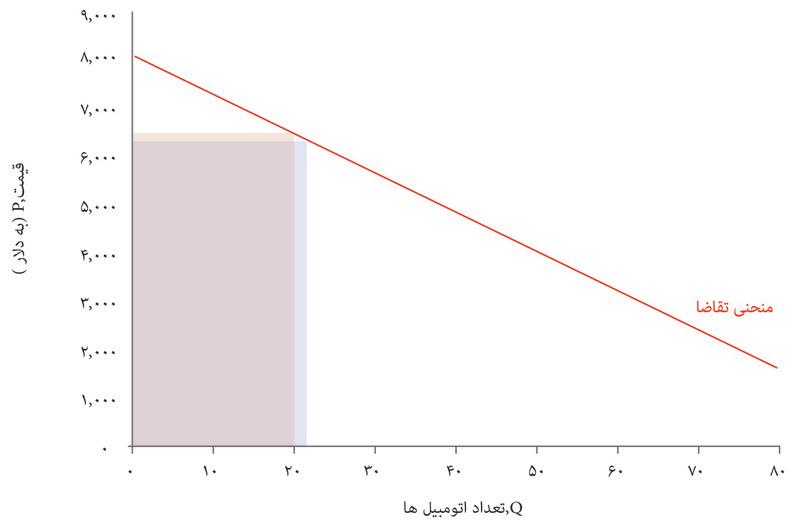
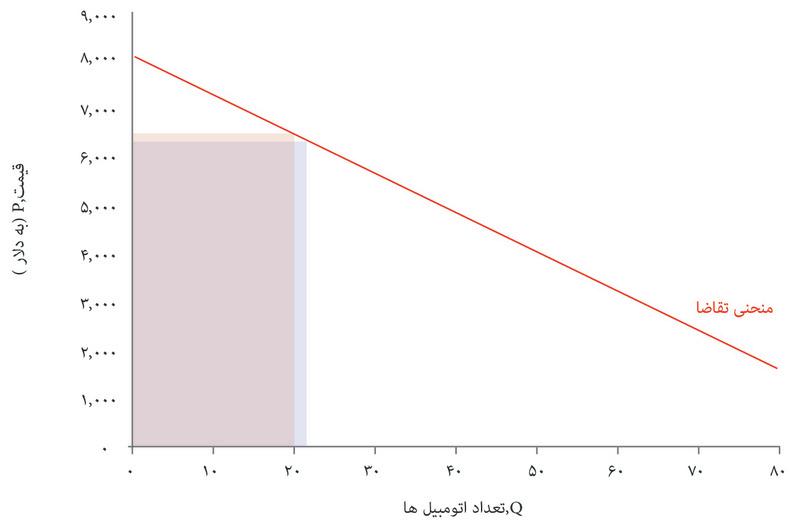
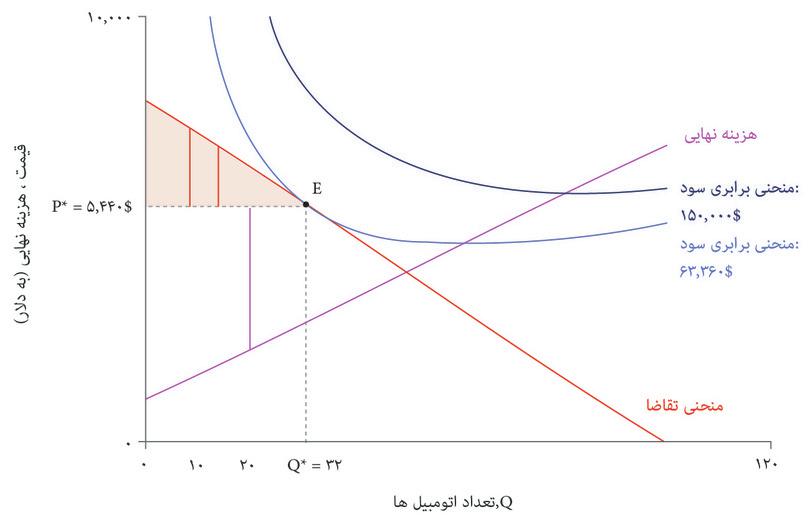
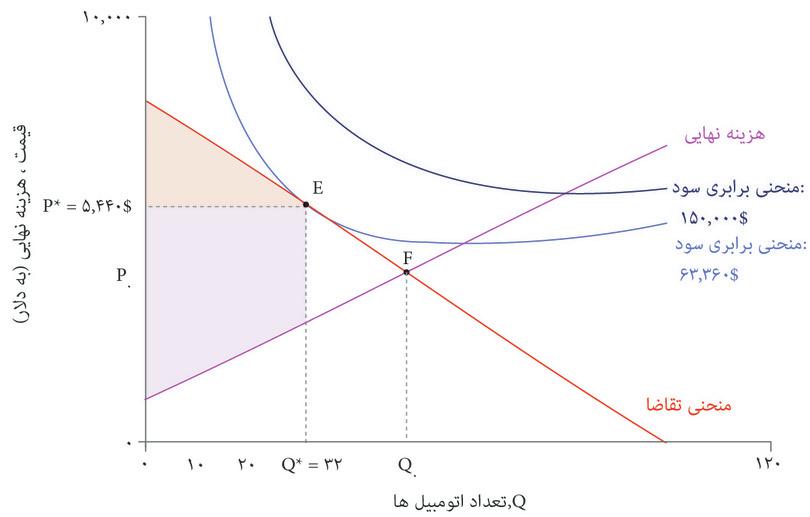
آیا تخصیص اتومبیلها در این بازار از کارایی پارتوییبرخوردار است؟ پاسخ منفی است، زیرا مصرفکنندگانی هستند که حاضر نسیتند اتومبیلها را به قیمت تعیین شده توسط بنگاه اقتصادی بخرند، اما حاضرند قیمتی بالاتر از هزینه تولید آنها برای شرکت پرداخت کنند. در شکل ۷.۱۳ دیدیم که بنگاههای اقتصادی مازادی بهازای آخرین اتومبیل تولید شده (یعنی اتومبیل سی و دوم) دریافت میکنند. قیمت بالاتر از هزینه نهایی است. بنگاه اقتصادی میتوانست یک اتومبیل دیگر هم تولید کند و با قیمتی کمتر از ۵۴۴۰ دلار اما بازهم بالاتر از هزینه تولید به سی و سومین مصرف کننده بفروشد. این یک بهبود پارتوییخواهد بود: هم بنگاه اقتصادی و هم مصرف کننده سی و سوم رفاه بیشتری خواهند داشت. بهعبارت دیگر، عواید بالقوه ناشی از معامله در بازار این نوع اتومبیل، در نقطه E به تمامی فعلیت نیافته است.
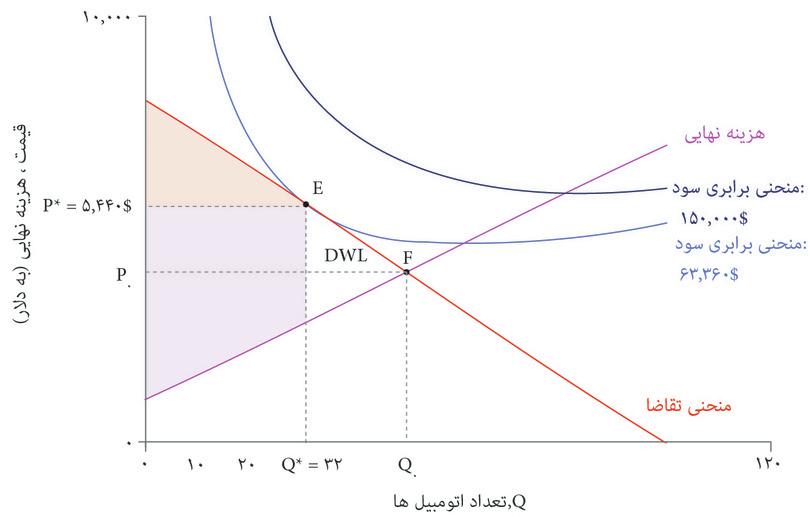
فرض کنید که بنگاه اقتصادی بجای آن نقطه F را انتخاب کند، یعنی جایی که منحنی هزینه نهایی، منحنی تقاضا را قطع میکند. این نقطه نشانگر یک تخصیص برخوردار از کارایی پارتویی است، که هیچ بهبود پارتویی بیشتری دیگر در آن ممکن نیست – یعنی تولید یک اتومبیل بیشتر هزینهای بیشتر از پرداخت همه الباقی مصرفکنندگان خواهد داشت. شکل ۷.۱۴ توضیح میدهد که چرا کل مازاد، که میتوانیم آن را کیکی تصور کنیم که باید میان بنگاه اقتصادی و مصرف کنندهها تقسیم شود، در نقطه F بالاتر خواهد بود.
در نقطه برخوردار از کارایی پارتویی F کل مازاد نسبت به نقطه E بالاتر خواهد بود. مازاد مصرف کننده بالاتر خواهد بود، زیرا کسانی که تمایل به خرید با قیمت بالاتر داشته اند از قیمت پایین بهره مند خواهند شد و مصرفکنندگان اضافی هم مازادی بدست خواهند آورد. اما شرکت اتومبیلهای زیبا نقطه F را انتخاب نخواهد کرد، چراکه مازاد تولید کننده در آن نقطه پایینتر است (و همانطور که میبینید روی منحنی برابری سود پایینتر قرار دارد).
- زیانِ ثابت
- کاهشِ مازادِ کل متناسب با یک تخصیصِ برخوردار از کارائیِ پارتوئی.
ازآنجاکه بنگاه اقتصادی نقطه E را انتخاب میکند، نوعی از دست دادن مازاد بالقوه وجود دارد که به آن زیان ثابتمیگوییم. روی نمودار، همان مساحت مثلثیای است که میان نقطه Q=۳۲ منحنی تقاضا و منحنی هزینه نهایی قرار دارد.
ممکن است بهنظر گیج کننده برسد که چگونه بنگاه اقتصادی نقطه E را انتخاب میکند در حالی که همانطور که گفته بودیم در این نقطه امکان مرفهتر شدنِ هم مصرف کننده و هم بنگاه اقتصادی وجود دارد. این درست است، اما تنها در صورتی که بتوان به دیگر مصرفکنندگان با قیمتی پایینتر از ۳۲ مصرف کننده اولیه اتومبیل فروخت. بنگاه اقتصادی نقطه E را انتخاب میکند چراکه در چارچوب قواعد بازی (یعنی تعیین یک قیمت یکسان برای همه مصرفکنندگان) بهترین گزینه محسوب میشود. تخصیصی که از قیمت گذاری تولیدکننده کالای متمایز و خاصی چون اتومبیلهای زیبا، فاقد کارایی پارتویی است. بنگاه اقتصادی با استفاده از قدرت چانهزنی خود تلاش میکند قیمتی بالاتر از هزینه نهایی یک اتومبیل تعیین کند. او با تولید تعداد بسیار کم، قیمت را براساس تخصیص برخوردار از کارایی پارتویی، بالا نگه میدارد.
بهعنوان یک آزمایش فکری تصور کنید که قواعد بازی متفاوت بودند و بنگاه اقتصادی میتوانست قیمتهای مجزایی برای هر خریدار تعیین کند، قیمتی اندکی پایینتر از مقدار تمایل به پرداخت خریدار. در آن صورت بنگاه اقتصادی قطعاً میتوانست به هر خریدار بالقوهای که تمایل به پرداختش از هزینه نهایی بالاتر باشد بفروشد و در نتیجه همه معاملات متقابلاً سودآور اتفاق میافتاد. تعدادی از اتومبیل تولید میکرد که کارایی پارتویی داشت.
اگر بهاین شیوه قیمتهای مجزا و جداگانه تعیین کنیم (که به آن تبعیض قیمتی میگویند)، بنگاه اقتصادی باید بتواند تمایل به پرداخت هر خریدار را بداند. در این مورد فرضی، زیان ثابت از میان خواهد رفت. بنگاه اقتصادی کل مازاد را به چنگ خواهد آورد: مازاد تولیدکننده وجود خواهد داشت اما نه مازاد مصرف کننده. ممکن است فکر کنیم این ناعادلانه است اما تخصیص بازار کارایی پارتویی خواهد داشت.
تمرین ۷.۵ تغییر قواعد بازی
- تصور کنید شرکت اتومبیلهای زیبا آنقدر قدرت چانهزنی داشت که میتوانست برای هر مصرف کننده، بطور جداگانه، قیمتی برابر با حداکثر تمایل به پرداخت آنها تعیین کند. منحنیهای تقاضا و هزینه نهایی را (مثل شکل ۷.۱۴) ترسیم کنید و موارد زیر را روی نمودارتان نشان دهید:
- تعداد اتومبیلهای فروخته شده
- بالاترین قیمت پرداخت شده توسط هر مشتری
- کمترین قیمت پرداخت شده
- مازاد مصرف کننده و تولید کننده
- آیا میتوانید نمونههایی از کالاهایی را که بهاین صورت فروخته میشوند ذکر کنید؟
- چرا این شیوه عمومیت ندارد؟
- برخی بنگاههای اقتصادی برای گروههای مختلف مشتریان خود قیمتهای متفاوتی تعیین میکنند – مثلاً خطوط هواپیمایی ممکن است جریمه بیشتری برای مسافران لحظه آخری اعمال کنند. چرا این کار را میکنند و اینکار چه تأثیری بر تقسیم مازاد میگذارد؟
- قواعد بازی دیگری را پیشنهاد کنید که به مصرف کننده قدرت چانهزنی بیشتری بدهد.
- تحت این قوانین، چه تعداد اتومبیل فروخته خواهد شد؟
- تحت این قوانین، مازاد مصرف کننده و تولیدکننده چقدر خواهد بود؟
پرسش ۷.۱۳ (یک پاسخ را انتخاب کنید).
کدامیک از گزارههای زیر صحیح است؟
- (الف) این درست است: بهعبارت دقیقتر، هر مصرفکننده مازادی معادلِ مابه التفاوتِ میان WTP و قیمت دریافت میکند، و مازاد مصرفکننده حاصل جمع مازادهای همه مصرفکنندگان است.
- (ب) مازاد تولیدکننده عبارت است از تفاوت میان درآمدِ بنگاه اقتصادی و هزینههای نهایی آن. این با سود یکسان نیست، زیرا هزینه ثابتِ تولید را در نظر نمیگیرد. سود عبارت است از مازاد تولیدکننده منهای هزینههای ثابت.
- (ج) زیان ثابت، خسارتِ مازاد کلی است که بطور بالقوه و بدلیلِ تولید بنگاه اقتصادی در سطحی پائینتر از سطحِ کارایی پارتویی از دست میرود. زیان ثابت حاصل جمع مازادهای ازدست رفته مصرفکنندگان و تولیدکننده است.
- (د) در سطحِ خروجیِ برخوردار از کارایی پارتویی، کلیه عوایدِ ممکن بدست میآیند. اما انتخاب به حداکثررساننده سود از جانبِ بنگاه اقتصادیای که یک کالای متمایز تولید میکند، کارایی پارتویی ندارد.
۷.۸ کشسانی تقاضا
بنگاه اقتصادی با انتخاب نقطهای سود خود را به حداکثر میرساند که در آن شیب منحنی برابری سود (MRS) با شیب منحنی تقاضا (MRT) برابر است؛ این نقطه نشانگر بده-بستانی است که بنگاه اقتصادی مقید است بین قیمت و تعداد ایجاد کند.
- کشسانیِ قیمتیِ تقاضا
- درصدِ تغییر در تقاضایی که در پاسخ به یک درصد افزایشِ قیمت اتفاق میافتد. این را در قالب یک عدد مثبت نشان میدهیم. اگر این عدد بالاتر از یک باشد تقاضا کشسان و اگر کمتر از یک باشد ناکشسان است.
بنابراین تصمیم بنگاه اقتصادی بستگی به این خواهد داشت که شیب محنی تقاضا چقدر باشد: بهعبارت دیگر، تقاضای مصرف کننده برای یک کالا، با تغییر قیمت کالا، چقدر تغییر میکند. کشسانی قیمتی تقاضا سنجهای است از پاسخگویی مشتریان به تغییر قیمتی: آن را بهشکل درصد تغییری در تقاضا که در نتیجه ۱ درصد افزایش قیمت رخ میدهد نشان میدهند. برای مثال فرض کنید که با یک افزایش ۱۰ درصدی در قیمت یک کالا، شاهد یک سقوط ۵ درصدی در تعداد فروش آن هستیم. در این صورت میتوان کشسانی، یعنی ε، را بهشکل زیر محاسبه کرد:
ε همان پنجمین حرف الفبای یونانی است که غالباً برای نشان دادن کشسانی از آن استفاده میشود. در یک منحنی تقاضا، تعداد، با افزایش قیمت سقوط میکند. بنابراین تغییر در تقاضا، در صورتی که تغییر قیمت مثبت باشد، منفی است و بالعکس. علامت منها در فرمول کشسانی برای این است که عددی که به عنوان سنجه پاسخگویی بدست میآوریم حتماً مثبت باشد. بنابراین در این مثال به عدد ۰.۵ میرسیم:
کشسانی قیمتی تقاضا به شیب منحنی تقاضا مربوط میشود: اگر منحنی تقاضا کاملاً تخت باشد، تعداد، در پاسخ به تغییر در قیمت، تغییر زیادی میکند و بنابراین کشسانی بالاست. بالعکس، یک منحنی تقاضای پرشیبتر، کشسانی کمتری به همراه دارد. اما اینها یک چیز نیستند، و مهم است که فراموش نکنیم که هرچه روی منحنی تقاضا به سمت جلو حرکت میکنیم، کشسانی هم تغییر میکند، حتی اگر شیب هم تغییر نکند.
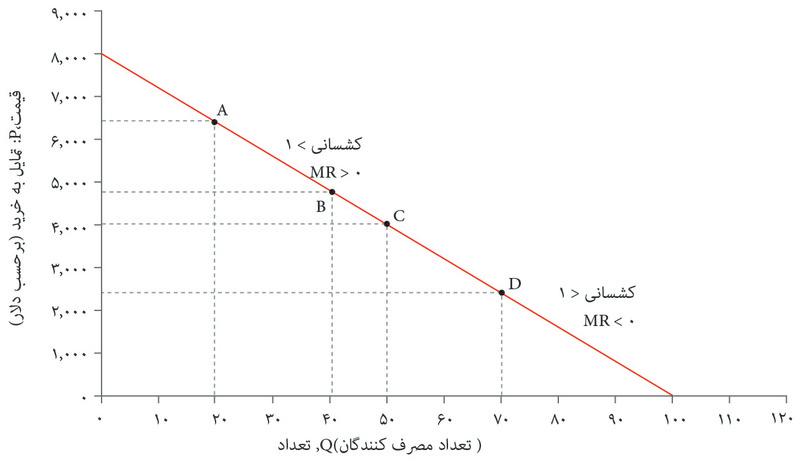
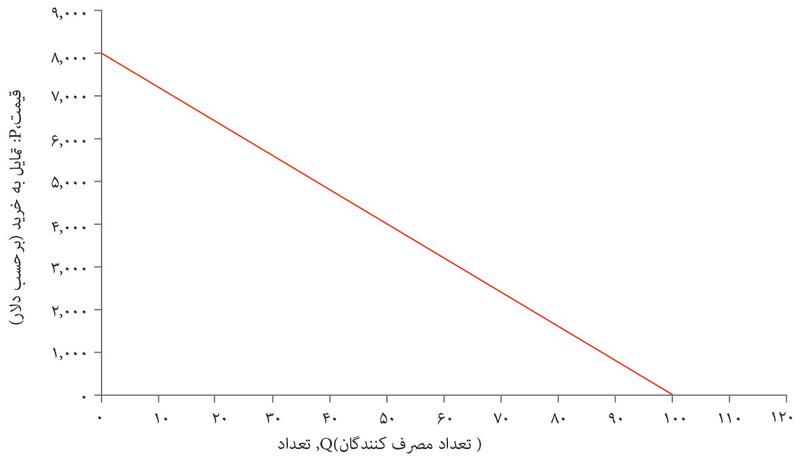
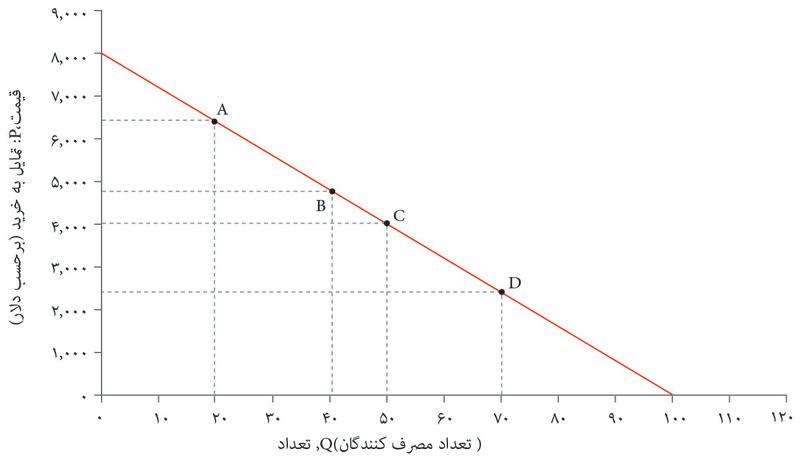
شکل ۷.۱۵ بازهم منحنی تقاضای اتومبیلها را نشان میدهد، که شیب ثابتی دارد: یک خط مستقیم است. در هر نقطه، اگر تعداد بهاندازه ۱ واحد افزایش پیدا کند(ΔQ = ۱), قیمت بهاندازه ۸۰ دلار کاهش پیدا میکند، (ΔP = –$۸۰):
تغییر قیمت ۸۰- دلار است ΔP = −$۸۰هرگاه تغییر تعداد روی هر نقطه از منحنی تقاضا برابر با ۱ واحد باشد ΔQ = ۱ محاسبه کشسانی در هر نقطه هم آسان است. برای مثال در نقطه A ، یعنی نقطه تعداد ۲۰ و قیمت ۶۴۰۰. به این صورت:
و همچنین
جدول شکل ۷.۱۵ کشسانی چندین نقطه روی منحنی تقاضا را محاسبه کرده است. میتوانید به کمک خطوط جانبی ببینید که هرچه ما روی منحنی تقاضا به سمت جلو حرکت میکنیم، مقدار یکسانی از تغییر در قیمت و تعداد، به درصد تغییرِ بالاتری در قیمت و درصد تغییر پایینتری در تعداد میانجامد، و بنابراین کشسانی کاهش پیدا میکند.
اگر کشسانی بالاتر از ۱ باشد میگوییم تقاضا کشسان است و اگر پایینتر از ۱ باشد میگوییم ناکشسان است. از روی جدول شکل ۷.۱۵ میتوانید ببینید که درآمد نهایی در نقاطی که تقاضا کشسان است، مثبت و هرجا که ناکشسان است منفی است. چرا چنین اتفاقی میافتد؟ وقتی تقاضا کشسانی بالایی دارد، با افزایش تعداد قیمت تنها اندکی کاهش پیدا خواهد کرد. بنابراین با تولید یک اتومبیل اضافی، بنگاه اقتصادی بهازای آن اتومبیل اضافی درآمد خواهد داشت بیآنکه چیز زیادی روی اتومبیلهای دیگر از دست داده باشد و بهاین ترتیب درآمد کل افزایش پیدا خواهد کرد؛ بهعبارت دیگر، MR > صفر است. برعکس، اگر تقاضا ناکشسان باشد، بنگاه اقتصادی نمیتواند تعداد را بدون یک کاهش جدی در قیمت بالا ببرد، بنابراین MR < صفر است. در انیشتین این قسمت، نشان میدهیم که این رابطه در مورد همه منحنیهای تقاضا صدق میکند.
پرسش ۷.۱۴ (همه پاسخ های صحیح را انتخاب کنید).
فروشگاهی ۲۰ کلاه در هفته و هرکدام را به قیمت ۱۰ دلار میفروشد. وقتی قیمت را به ۱۲ دلار افزایش دهد، تعداد کلاههای فروخته شده به ۱۵ کلاه در هفته کاهش پیدا میکند. کدامیک از گزارههای زیر صحیح است؟
- (الف) وقتی قیمت از ۱۰ به ۱۲ دلار افزایش پیدا می کند، تقاضا کاهش پیدا می کند.
- (ب) درصدی که قیمت افزایش پیدا می کند عبارتست از ۱۰۰ × ۲/۱۰ = ۲۰%. این باعثِ یک کاهش ۲۵ درصدی ۱۰۰ × ۵/۲۰ = ۲۵% در تقاضا می شود.
- (ج) استفاده از اشکال، کشسانیِ قیمتیِ تقاضا را بیشتر از ۱ نشان می دهد پس تقاضا کشسان است.
- (د) درصدی که قیمت افزایش پیدا می کند عبارتست از ۱۰۰ × ۲/۱۰ = ۲۰%; کاهش درصدی در تقاضا ۱۰۰ × ۵/۲۰ = ۲۵%. است. بنابراین کشسانی بصورت تخمینی عبارت است از ۲۵/۲۰=۱.۲۵.
کشسانی تقاضا چه تأثیری بر تصمیمات بنگاه اقتصادی دارد؟ بیاد داشته باشید که تعداد به حداکثررساننده ی سود برای تولید کننده اتومبیل ۳۲ است. در شکل ۷.۱۵ میتوانید ببینید که این نقطه در قسمت کشسان منحنی تقاضا قرار دارد. بنگاه اقتصادی هیچگاه تمایلی به انتخاب نقطهای مثل D نخواهد داشت، زیرا در این نقطه منحنی ناکشسان است چراکه درآمد نهایی منفی است؛ همیشه بهتر خواهد بود که تعداد را کاهش دهیم، زیرا اینکار درآمد را افزایش و هزینهها را کاهش خواهد داد. بنابراین بنگاه اقتصادی همیشه نقطهای را انتخاب میکند که در آن کشسانی بالاتر از ۱ باشد.
- حاشیه سود
- تفاوت بین قیمت و هزینه نهایی.
دوم اینکه حاشیه سود بنگاه اقتصادی (یعنی تفاوت میان قیمت و هزینه نهایی تولید) شدیداً به کشسانی تقاضا وابسته است. شکل ۷.۱۶ یک وضعیت برخوردار از کشسانی بسیار بالا را نشان میدهد. منحنی تقاضا کاملاً تخت است، بنابراین کوچکترین تغییر در قیمت هم تفاوت بزرگی در فروش برجای میگذارد. انتخاب به حداکثررساننده سود نقطه E است. میتوانید ببینید که حاشیه سود نسبتاً کوچک است. این به آن معناست که تعداد اتومبیلی که بنگاه اقتصادی برای تولید انتخاب میکند، خیلی پایینتر از تعداد برخوردار از کارایی پارتویی، یعنی نقطه F که در آن حاشیه سود صفر است، نیست.
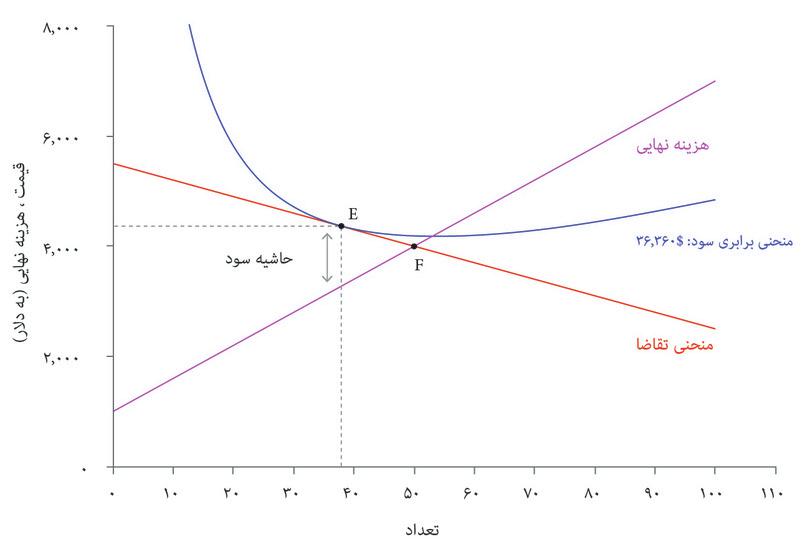
شکل ۷.۱۶ بنگاه اقتصادیی که با تقاضای بسیار کشسان روبهرو است.
شکل ۷.۱۷ نشان میدهد که بنگاه اقتصادیی با همین هزینههای تولید اتومبیل، اما با کشسانی کمتر در تقاضا برای محصولات، چه تصمیماتی خواهد گرفت. در این مورد حاشیه سود بالاست، و تعداد پایین است. وقتی قیمت افزایش داده میشود، بسیاری از مصرفکنندگان همچنان تمایل به پرداخت دارند. بنگاه اقتصادی به بهره کشی از این وضعیت، سود خود را به حداکثر میرساند و سهم بیشتری از مازاد بدست میآورد، اما نتیجه این است که اتومبیلهای کمتری فروخته میشوند و عواید بهره کشی نشده ناشی از مبادله، که زیان ثابت آن را نشان میدهد، همچنان بسیار زیاد است.
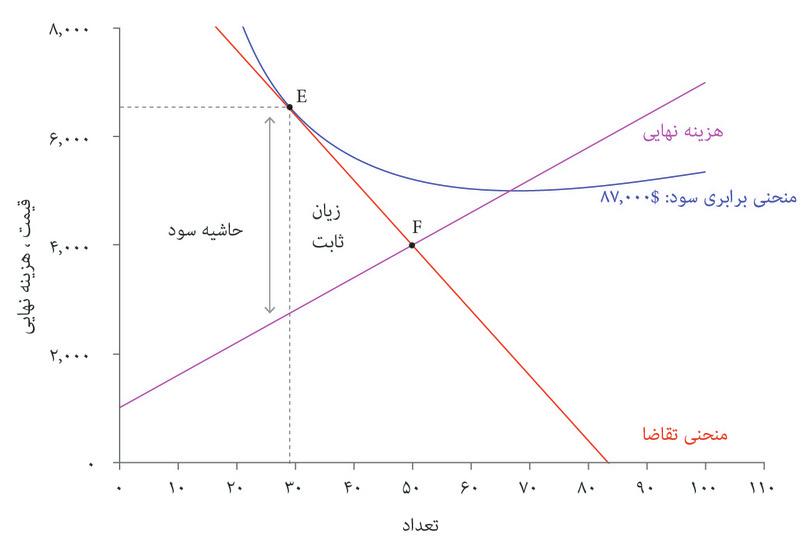
شکل ۷.۱۷ بنگاه اقتصادیی که با کشسانی تقاضای بسیار پایین رو بهرو است.
- مابهالتفاوتِ قیمت
- قیمت منهای هزینهی نهایی تقسیم بر قیمت. که با کشسانیِ تقاضا برای این کالا نسبت معکوس دارد.
لایبنیتز: کشسانی تقاضا
این مثالها نشان میدهند که هرچه کشسانی تقاضا کمتر باشد، بنگاه اقتصادی به مقدار بیشتری قیمت را از سطح هزینههای نهایی بالاتر خواهد برد تا حاشیه سود بالاتری بدست بیاورد. وقتی کشسانی تقاضا پایین است، بنگاه اقتصادی این قدرت را دارد که میتواند قیمت را بدون اینکه مشتریان زیادی از دست بدهد بالا ببرد، و افزایش بها, که همان حاشیه سود بصورت نسبتی از قیمت است، بالا خواهد بود. انیشتین پایان این فصل به شما نشان میدهد که افزایش بها نسبت معکوسی با کشسانی تقاضا دارد.
پرسش ۷.۱۵ (همه پاسخهای صحیح را انتخاب کنید)
شکل زیر دو منحنی تقاضا را نشان میدهد، D1 و D2.
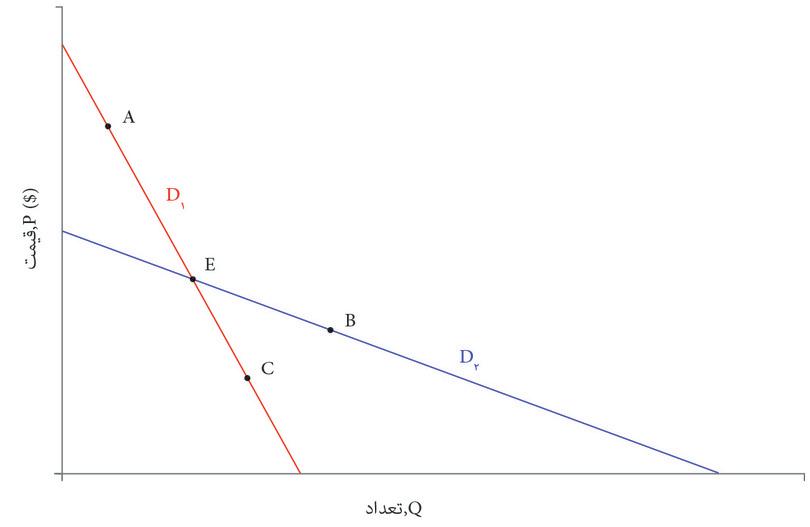
براساس این شکل، کدامیک از گزارههای زیر صحیح است؟
- (الف) در نقطه E قیمت و تعداد روی هر دو منحنی یکسان اند، اما D1 پرشیب تر است، و بنابراین کشسانی کمتری نسبت به D2 دارد.
- (ب) شیب در نقطه A و C هر دو یکسان است، اما در نقطه A قیمت بالاتر و تعداد پائین تر است و بنابراین کشسانی بالاتر است.
- (ج) قیمت و تعداد روی هر دو منحنی تقاضا یکسانند، اما D1 شیب بیشتری دارد و بنابراین کشسانی ها با هم برابر نیستند.
- (د) شیب در نقطه E و C یکسان است. اما در نقطه E قیمت بالاتر و تعداد پائین تر است و بنابراین کشسانی بالاتر است.
انیشتین کشسانی تقاضا و عواید نهایی
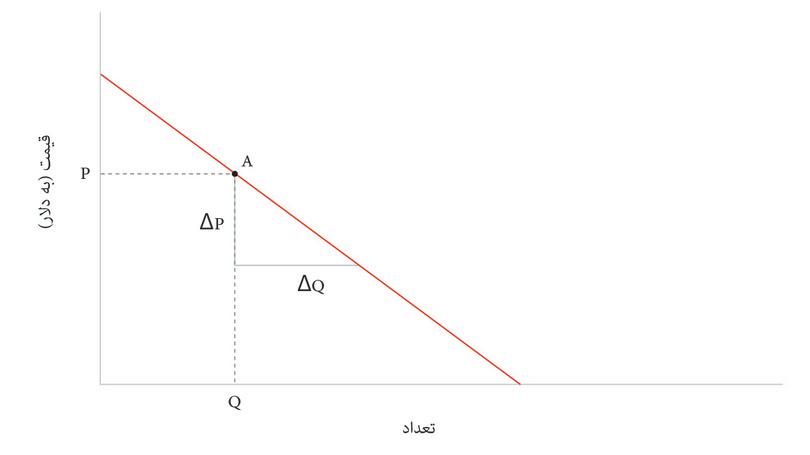
نمودار نشان میدهد که چگونه میتوان یک فرمول کلی برای کشسانی در یک نقطه (Q،P) روی منحنی پیدا کنید.
همچنین نشان میدهد که چگونه کشسانی به شیب منحنی تقاضا بستگی دارد. یک منحنی تقاضای تختتر، شیب کمتر و بنابراین کشسانی بالاتری دارد.
![کشسانی تقاضا و درآمد نهایی.]()
شکل ۷.۱۸ کشسانی تقاضا و درآمد نهایی.
در نقطه A، قیمت P و کیفیت Q است. اگر کیفیت با ΔQ افزایش پیدا کند، قیمت کاهش پیدا میکند: قیمت با ΔP تغییر میکند، که منفی است.
فرض کنید که منحنی تقاضا در نقطه A کشسان است. در این صورت کشسانی بزرگتر از ۱ است:
که اگر آن را در −QΔP (که یک مقدار مثبت است) ضرب کنیم:
و در نهایت به این عبارت میرسیم:
حالا به مورد ویژهای توجه کنید که در آن ΔQ = ۱ است. نابرابری بصورت زیر درمیآید:
حالا بیاد بیاورید که درآمد نهایی در نقطه A عبارت است از تغییر درآمدی که با افزوده شدن تعداد بهاندازه یک واحد حاصل میشود. این تغییر عبارت است از عایدیِ درآمدیای که روی یک واحد تولید اضافه بدست آمده است، که همان Pاست، و خسارتی که روی واحدهای دیگر تولید متحمل شده است، که همان QΔPاست. بنابراین، این نابرابری به ما میگوید که درآمد نهایی مثبت است.
ما نشان دادهایم که اگر منحنی تقاضا کشسان باشد، MR > صفر خواهد بود؛ به همین طریق، اگر منحنی تقاضا ناکشسان باشد، MR < صفر خواهد بود.
اندازه تفاوت بهای انتخاب شده توسط بنگاه اقتصادی
میتوانیم فرمولی پیدا کنیم که نشان میدهد هرگاه کشسانی تقاضا پایین است، تفاوت بها بالا است.
میدانیم که بنگاه اقتصادی نقطهای را انتخاب میکند که در آن شیب منحنی برابری سود با سیب منحنی تقاضا برابر باشد، و نیز اینکه شیب منحنی تقاضا به کشسانی قیمتی تقاضا مربوط میشود:
که میتوانیم آن را بصورت فرمول زیر بازآرایی کنیم:
همچنین از بخش ۷.۴ بیاد داریم که:
وقتی دو شیب برابر هستند:
که با بازنویسی آن به این فرمول میرسیم:
نیمه سمت چپ، حاشیه سود را بصورت نسبتی از قیمت بیان میکند که به آن تفاوت بها میگویند. بنابراین:
تفاوت بهای بنگاه اقتصادی، با کشسانی تقاضا نسبت معکوس دارد.
۷.۹ کاربرد کشسانی تقاضا در سیاست گذاریهای دولتی
اندازهگیری کشسانیهای تقاضا برای سیاستگذاران بسیار مفید است. اگر دولت مالیاتی بر یک کالای خاص بگذارد، این مالیات قیمت پرداختی مصرف کننده را افزایش میدهد، بطوری که تأثیری مالیات وابسته به کشسانی تقاضا خواهد بود.
- اگر تقاضا بسیار کشسان است: مالیات کاهش بزرگی در فروش را بدنبال خواهد داشت. اینکار ممکن است تعمداً صورت بگیرد، مثل وقتی که دولتها برای مبارزه با دخانیات که برای سلامتی مضر است، برای تنباکو مالیاتهایی وضع میکنند.
- اما اگر مالیات اُفت چشمگیر فروش را در پی دارد: پس درآمدهای مالیاتی بالقوه را نیز کاهش میدهد.
بههمین علت دولتی که میخواهد درآمدهای مالیاتیاش را بالا ببرد، باید برای محصولاتی مالیات وضع کند که تقاضای ناکشسان دارند.
بسیاری از کشورها، منجمله فرانسه و دانمارک، اخیراً مالیاتهای جدیدی وضع کرده اند که هدف از آنها کاهش مصرف خوردنیها و آشامیدنیهای ناسالم است. یک مطالعه بین المللی در سال ۲۰۱۴ به افزایش نگران کننده چاقی بزرگسالان و کودکان از سال ۱۹۸۰ به این سو برخورد. در سال ۲۰۱۳، ۳۷ درصد از مردان و ۳۸ درصد از زنان در سرتاسر جهان اضافه وزن یا چاقی داشته اند. در آمریکای شمالی همین ارقام ۷۰ و ۶۱ درصد بوده است، اما اپیدمی چاقی تنها بر ثروتمندترین کشورها تأثیر نمیگذارد: در خاورمیانه و شمال آفریقا نیز این ارقام ۵۹ و ۶۱ درصد بوده اند.
متیو هاردینگ و میکائیل لوونهایم ریزدادههای مربوط به خریدهای غذایی مصرفکنندگان آمریکایی را بررسی کرده و کشسانی تقاضا برای انواع مختلف غذا را با هدف بررسی تأثیرات مالیاتهای غذایی تخمین زده است. آنها محصولات غذایی را به ۳۳ مقوله تقسیم بندی کردند و براساس یک الگوی تصمیمگیری مصرف کننده تلاش کردند تا مشخص کنند که تغییر در قیمتها چه تأثیری بر سهم هر مقوله در هزینهکرد غذایی مصرف کننده، و درنتیجه بر ترکیب تغذیهای رژیم آنها خواهد داشت، با در نظر گرفتن این نکته که تغییر در قیمت هر محصول، تقاضا برای آن محصول و محصولات دیگر را نیز تغییر میدهد. شکل ۷.۱۸ قیمت و کشسانیهای مربوط به برخی از این مقولات را نشان میدهد:
| دستهبندی | نوع | کالری هر وعده | قیمت هر ۱۰۰ گرم ($) | هزینه معمولی هر هفته ($) | قیمت کشسانی تقاضا |
|---|---|---|---|---|---|
| ۱ | میوه و سبزیحات | ۶۶۰ | ۰،۳۸ | ۲،۰۰ | ۱،۱۲۸ |
| ۲ | میوه و سبزیحات | ۱۴۰ | ۰،۳۶ | ۳،۴۴ | ۰،۸۳۰ |
| ۱۵ | غلات، پاستا، نان | ۱۵۴۰ | ۰،۳۸ | ۲،۹۶ | ۰،۸۵۴ |
| ۱۷ | غلات، پاستا، نان | ۹۶۰ | ۰،۵۳ | ۲،۶۴ | ۰،۲۹۲ |
| ۲۸ | تنقلات و آبنبات | ۴۳۳ | ۱،۱۳ | ۴،۸۸ | ۰،۲۷۰ |
| ۲۹ | تنقلات و آبنبات | ۱۷۲۷ | ۰،۶۸ | ۷،۶۰ | ۰،۲۹۵ |
| ۳۰ | شیر | ۲۰۵۲ | ۰،۰۹ | ۲،۳۲ | ۱،۱۷۹۳ |
| ۳۱ | شیر | ۸۷۴ | ۰،۱۵ | ۱،۴۴ | ۱،۹۷۲ |
شکل ۷.۱۹ کشسانی قیمتی تقاضا برای انواع مختلف غذا. براساس جدول کالریها، گروههای پرکالری و کمکالری هر نوع غذا را با هم مقایسه کنید.
Matthew Harding and Michael Lovenheim. 2013. ‘The Effect of Prices on Nutrition: Comparing the Impact of Product- and Nutrient-Specific Taxes’. SIEPR Discussion Paper No. 13-023.
ملاحظه میکنید که تقاضا برای محصولات شیریِ کم کالری، بیشتر از همه به قیمت واکنش نشان میدهد. اگر قیمتشان ۱۰ درصد افزایش پیدا کند، تعداد خریداری شده بهاندازه ۱۹،۷۲ درصد کاهش پیدا میکند. تقاضا برای اسنک و آبنبات کاملاً غیرکشسان است، که بهاین معناست که احتمالاً بازداشتن مصرف کننده از خرید آن دشوار خواهد بود.
تمرین ۷.۶ کشسانی و هزینهکرد
شکل ۷.۱۹ همچنین پرداختی هفتگی برای هر کدام از مقولات غذایی یک مصرف کننده آمریکایی را نیز نشان میدهد، مصرف کنندهای که کل پرداختیاش در اقلام غذایی ۸۰ دلار است و الگوهای پرداختی معینی در همه مقولات غذایی دارد. فرض کنید که قیمت مقوله سی ام، محصولات شیری پرکالری، ۱۰ درصد افزایش پیدا کند:
- در این صورت تقاضای این مصرف کننده برای محصولات شیری پرکالری چند درصد کاهش خواهد داشت؟
- تعداد مصرفی او را، برحسب گرم، قبل و بعد از افزایش قیمت محاسبه کنید.
- کل هزینهکرد او برای محصولات شیری پرکالری را قبل و بعد از افزایش قیمت محاسبه کنید. قاعدتاً به کاهش هزینهکرد خواهید رسید.
- حالا مقولهای را انتخاب کنید که کشسانی قیمتی آن کمتر از ۱ باشد، و این محاسبات را تکرار کنید. در این مورد قاعدتاً باید به افزایش هزینهکرد برسید.
هاردینگ و لوونهایم، تأثیر مالیاتهای ۲۰ درصدی بر شکر، چربی و نمک را بررسی کردند. مثلاً یک مالیات ۲۰ درصدی شکر، قیمت محصولی را که حاوی ۵۰ درصد شکر است، بهاندازه ۱۰ درصد افزایش میدهد. معلوم شد که مالیات شکر مثبتترین تأثیر بر تغذیه را داشته است. مصرف شکر را بهاندازه ۱۶ درصد، چربی را ۱۲ درصد، نمک را ۱۰ درصد و کالری دریافتی را بهاندازه ۱۹ درصد کاهش میدهد. 6
For additional insight, this blog illustrates one reaction to Matthew Harding and Michael Lovenheim’s research: The Huffington Post. 2014. ‘There’s An Easy Way To Fight Obesity, But Conservatives Will HATE It’.
تمرین ۷.۷ مالیاتهای غذایی و بهداشت
مالیاتهای غذاییای که با هدف هدایت مصرف بهسمت رژیمهای غذایی سالمتر وضع میشوند، همواره محل مناقشه بوده اند. برخی بر این باورند که افراد باید انتخابهای خودشان را داشته باشند، و اگر غذاهای ناسالم را ترجیح میدهند، دولت نباید مداخله کند. با توجه به این نکته که مراقبت از افرادی که مریض میشوند مقداری هزینه عمومی بدنبال دارد، افراد دیگری هستند که مدعی هستند دولت باید در حفظ بهداشت مردم نقش داشته باشد.
به زبان خودتان، در موافقت یا مخالفت با مالیاتهایی که برای تشویق تغذیه سالم وضع میشوند، استدلال کنید.
۷.۱۰ قیمتگذاری، رقابت، و قدرت بازار
- انحصار
- شرکتی که تنها فروشنده کالایی است که جایگزینهای نزدیکی ندارد. همچنین به بازاری که تنها یک فروشنده دارد نیز اطلاق میشود. همچنین نگاه کنید به: قدرت انحصار، و انحصار طبیعی.
تحلیل ما از تصمیمات قیمتیِ بنگاه اقتصادی در مورد هر بنگاه اقتصادیی که کالایی تولید میکند و بفروش میرساند که حالا بهشکلی با کالای هر بنگاه اقتصادی دیگری متفاوت است نیز صدق میکند. در قرن نوزدهم اقتصاددان فرانسوی آگوستین کورنو تحلیل مشابهی را با استفاده از یک مثال انجام داد: آب بسته بندی شده ی «چشمهای معدنی که اخیراً معلوم شده خواص بهداشتیای دارد که در هیچ چشمه دیگری نیست»، کورنو این را نمونهای از انحصار—تلقی میکرد – و بازار انحصاری تنها یک فروشنده دارد. او هم مثل ما نشان داد که بنگاه اقتصادی قیمتی بالاتر از هزینه تولید نهایی اعلام خواهد کرد. 7
اقتصاددانان بزرگ آگوستین کورنو
آگوستین کورنو (۱۸۰۱ تا ۱۸۷۷) اقتصاددانی فرانسوی بود که امروزه بخاطر الگوی الیگارشی (بازاری با تعداد محدودی فروشنده) شهرت دارد. کتاب تحقیق درباب اصول ریاضیاتیِ نظریه ثروت او در سال ۱۸۳۸ رویکرد ریاضیاتی جدیدی را به اقتصاد معرفی میکند، اگرچه نگران بود که این کتاب «سرزنشِ نظریه پردازان پرآوازه را نثارم خواهد کرد». کار کورنو بر اقتصاددانان قرن نوزدهمی دیگری ازقبیل مارشال و والراس تأثیر گذاشت، و اصول اولیهای را که ما همچنان رفتار بنگاههای اقتصادی را براساس آن میسنجیم بنا گذاشت. با اینکه کورنو از نمایش جبری استفاده میکرد و نه از نمودار، اما بازهم میبینیم که تحلیل کورنو از تقاضا و حداکثرسازی سود بسیار با تحلیل ما شباهت دارد.
در بخش ۷.۶ دیدیم که وقتی تولیدکننده یک کالای متمایز قیمتی بالای هزینه نهایی تولید اعلام میکند، درآمد بازار کارایی پارتویی نخواهد داشت. وقتی مبادلهای در بازار به یک تخصیص فاقد کارایی پارتویی منتهی میشود، ما این را نمونهای از شکست بازار تلقی میکنیم.
شکست بازار
شکست بازار هنگامی اتفاق میافتد که بازارها منابع را بهشکلی فاقد کارایی پارتویی توزیع میکنند.
زیان ثابت سنجهای برای فهم پیامدهای شکست بازار به ما میدهد: اندازه عواید بهره کشی نشده ناشی از مبادله. و درقسمت ۷.۷ دیدیم که زیان ثابت ناشی از تعیین قیمت بالاتر از هزینه نهایی، وقتی که کشسانی تقاضا پایین است، بالا است.
پس کشسانی تقاضا برای یک محصول را چه چیز تعیین میکند و چرا برخی بنگاههای اقتصادی بیشتر از بقیه با تقاضای کشسان روبرو میشوند؟ برای پاسخ به این سوال، باید نحوه رفتار مصرف کننده را یکبار دیگر بیاد بیاوریم.
بازاری با کالاهای متمایز، انعکاسی از ترجیحات مصرفکنندگان است. کسانی که قصد خرید اتومبیل دارند، بهدنبال ترکیبهای مختلفی از ویژگیها هستند. تمایل به پرداخت مصرف کننده برای یک مدل خاص تنها به ویژگیهای آن بستگی نخواهد داشت، بلکه به ویژگیها و قیمتهای انواع مشابه اتومبیل که توسط بنگاههای اقتصادی دیگر فروخته میشود نیز بستگی خواهد داشت.
برای مثال شکل ۷.۱۹ قیمت خرید یک هاچبک سه درهی ۱ لیتری در بریتانیا در ژانویه ۲۰۱۴ را که مصرف کننده میتوانست از روی وبسایت مقایسه قیمت پیدا کند نشان میدهد:
| قیمت | |
|---|---|
| فورد فیستا | £۱۱۹۱۷ |
| واکسهال کورسا | £۱۱۲۸۳ |
| پژو ۲۰۸ | £۱۰۳۸۴ |
| تیوتا IQ | £۱۱۲۵۴ |
شکل ۷.۲۰ قیمتهای خرید اتومبیل در بریتانیا (ژانویه ۲۰۱۴) منبع:Autotrader.com).
بااینکه هر ۴ اتومبیل ویژگیهای اصلی یکسانی دارند، اما وبسایت آنها را از نظر ۷۵ ویژگی غیر از آن که درمیان بسیاری از آنها متفاوت است مقایسه می کند.
وقتی مصرف کننده میتواند از میان چندین اتومبیل بسیار مشابه انتخاب کند، تقاضا برای هر کدام از این اتومبیلها بسیار کشسان خواهد بود. برای مثال اگر قیمت فوردِ فیِستا بالا برود، تقاضا کاهش خواهد یافت چراکه افراد بجای آن سراغ خرید یکی دیگر از برندها خواهند رفت. برعکس اگر قمت فورد سیستا کاهش پیدا کند، تقاضا افزایش پیدا خواهد کرد چراکه علاقه مصرفکنندگان را از اتومبیلهای دیگر بخود جلب خواهد کرد. هرچه سایر اتومبیلها شباهت بیشتری به فیستا داشته باشند، مصرفکنندگان هم نسبت به تفاوتهای قیمتی واکنش بیشتری خواهند داشت. تنها افرادی که بیشترین وفاداری برند را به فورد دارند، و افرادی که برخی ویژگیهای فورد را که در مدلهای مشابه وجود ندارد شدیداً ترجیح میدهند، واکنش یا پاسخی نخواهند داشت. پس بنگاه اقتصادی قیمت و حاشیه سود نسبتاً کمی خواهد داشت.
- رانتهای انحصاری
- شکلی از سود اقتصادی که از رقابتِ محدود در فروشِ کالای یک شرکت ناشی میشود. همچنین نگاه کنید به: سودِ اقتصادی.
در تقابل با این مثال، تولیدکننده یک نوع بسیار ویژه اتومبیل، که کاملاً با همه برندهای دیگری که در بازار هستند تفاوت دارد، با رقابت اندک و بنابراین تقاضای کمتر کشسانی روبهرو خواهد شد. میتواند بدون از دست دادن مشتری، قیمتی بسیار بالاتر از هزینه نهایی تعیین کند. بنگاه اقتصادی از بهره انحصاری (سود اقتصادی علاوه و بیش از هزینه تولید) برخوردار است، و این بهره از موقعیت شرکت بعنوان تنها ارائه دهنده این نوع اتومبیل ناشی میشود (بههمین ترتیب، یک بنگاه اقتصادی نوآور هم مادامی که تنها بنگاه اقتصادیی است که از یک فناوری جدید استفاده میکند از بهره برخوردار میشود: نگاه کنید به فصل ۲).
- نمونههای جایگزین
- دو کالایی که در آنها افزایش در قیمت هریک به افزایشِ تعداد تقاضا برای آن دیگری منجر میشود. همچنین نگاه کنید به: نمونههای مکمل.
- قدرتِ بازار
- یکی از خصلتهای شرکتی که میتواند محصولش را در محدودهای از قیمتهای مقرونبهصرفه بفروشد، بطوریکه قادر باشد (بجای قیمت-پذیربودن) بعنوان یک قیمت-گذار عمل کند و از آن سود ببرد.
پس یک بنگاه اقتصادی، وقتی بنگاه اقتصادیهای کمی هستند که جایگزینهایی شبیه به برندِ آن تولید کنند، در موقعیت قدرتمندی قرار میگیرد، چراکه با رقابت کمتری رو بهرو میشود. پس کشسانی تقاضای آن نسبتاً پایین خواهد بود. میگوییم که چنین بنگاه اقتصادیی اصطلاحاً از قدرت بازاربرخوردار است: یعنی در رابطه با مشتریان آن قدر قدرت چانهزنی دارد که بتواند بدون اینکه مشتریای را به رقبایش باخته باشد، قیمت بالا تعیین کند.
خط مشی رقابتی
این بحث به ما کمک میکند که توضیح دهیم چرا سیاستگذاران ممکن است در مورد بنگاههای اقتصادیی که رقبای کمی دارد نگرانیهایی داشته باشند. قدرت بازار به آنها اجازه میدهد که با قیمتهای بالا تعیین کنند، و سود زیادی ببرند، که البته به قیمت زیان مصرفکنندگان تمام میشود. مازاد مصرف کننده بالقوه از دست میرود، هم بهاین دلیل که مصرفکنندگان کمی خرید میکنند، و هم به این دلیل که کسانی که میخرند قیمت بالایی پرداخت میکنند. مالکان بنگاه اقتصادی سود میبرند، اما در مجموع زیان ثابت وجود دارد.
بنگاه اقتصادیی که یک کالای تزئینی میفروشد که ترجیحات مصرفکنندگان کمی را پوشش میدهد (مثلاً اتومبیلهای زیبا یا برند لوکسی مثل لامبورگینی)، علیرغم مازاد مصرف کنندهای که از دست میدهد، اما توجه سیاستگذاران را به خود جلب نخواهد کرد. اما اگر بنگاه اقتصادیی در حال تسلط در یک بازار بزرگ باشد، ممکن است دولتها برای بهبود رقابت دست به مداخله بزنند. در سال ۲۰۰۰ کمیسیون اروپا پیشنهاد تلفیق دو شرکت ولوو و اسکانیا را رد کرد، چراکه این بنگاه اقتصادی تلفیق جایگاه مسلطی در بازار کامیونهای سنگین در ایرلند و کشورهای شمال اروپا پیدا میکرد. در سوئد سهم بازار مجموع این دو بنگاه اقتصادی ۹۰ درصد بود. بنگاه اقتصادی تلفیق شده تقریباً به یک انحصار بدل میشد – یعنی نمونه اعلای بنگاه اقتصادیی که هیچ رقیبی ندارد.
- کارتل
- گروهی از شرکتهایی که با یکدیگر تبانی میکنند تا سودِ مشترکشان را بالا ببرند.
مشخصاً یکی از دغدغهها این است که وقتی تنها چند بنگاه اقتصادی معدود در یک بازار هستند، میتوانند به یک کارتلتبدیل شوند: یعنی گروهی از بنگاههای اقتصادی که برای بالا نگه داشتن قیمتها با هم تبانی میکنند. آنها میتوانند بجای رقابت کردن با یکدیگر، با هم و بعنوان یک انحصار کار و رفتار کنند، و سودشان را بالا ببرند. یک مثال مشهور اپک OPECاست, سازمان کشورهای تولیدکننده نفت. اعضای اپک بطور جمعی برای کنترل قیمت جهانی نفت بر سر قیمتها توافق میکنند. کارتل اوپک نقش مهمی در تقویت قیمت بالای نفت در سطح جهانی بدنبال افزایشهای شدید سال ۱۹۷۱ و مجدداً در سال ۱۹۷۹ بازی کرد. در فصل ۱۵ دوباره به شوکهایی که قیمت نفت بر تورم و بیکاری دارد برخواهیم گشت.
- خطمشیِ رقابتی
- خطمشیِ دولتی و قوانینِ معطوف به محدودسازی قدرتِ انحصار و ممانعتِ از شکلگیری کارتلها. همچنین تحتِ عنوانِ خطمشیهایِ آنتیتراست هم شناخته میشوند.
ازآنجاکه تشکیل کارتل میان بنگاههای اقتصادی خصوصی در بسیاری از کشورها غیرقانونی است، بنگاههای اقتصادی غالباً راههایی پیدا میکنند که در تعیین قیمتها با هدف حداکثرسازی سود بهنوعی مشارکت داشته باشند. خط مشی معطوف به محدودکردن قدرت بازار و پیشگیری از تشکیل کارتلها را با عنوان خط مشی رقابتی، یا در ایالات متحده خطمشی ضدتراست مینامیم.
بنگاههای اقتصادی مسلط ممکن است موقعیت خود را با راهبردهایی غیر از قیمت بالا بدست آورند. در یک مورد مشهور آنتیتراست، وزارت عدالت آمریکا مایکروسافت را متهم کرد که با الحاقِ مرورگرِ وب خود به سیستم عامل ویندوز رفتاری ضدرقابتی داشته است. در دهه ۱۹۲۰ یک گروه بین المللی از شرکت های تولیدکننده لامپهای الکتریکی، شامل فیلیپس، اسرام، و جنرال الکتریک کارتلی را تشکیل دادند که توافق کردند که یک سیاست «از رده خارجسازی برنامه ریزی شده» را دنبال کنند: با این هدف که بتوانند طول عمر لامپهای خود را تا ۱۰۰۰ ساعت کاهش دهند بطوریکه مصرفکنندگان ناچار باشند زودتر آنها را عوض کنند. برخی از مردم هم شرکت والمارت را متهم میکنند که علیرغم شعار «همیشه ارزانتر»اش گاهی از قدرت خود بهشکل غیرعادلانه استفاده میکند و دستمزدها را در نواحی نزدیک به انبارهایش کاهش میدهد، خرده فروشان کوچک تر را به بیرون از بازار میراند، یا سود کارپردازان عمده فروش را تا سطوح غیرپایداری کاهش میدهد. این مقاله مبنای اقتصادی این مدعیات را بررسی میکند.8
تمرین ۷.۸ چندملیتیها یا خرده فروشان مستقل؟
تصور کنید که یک سیاستمدار هستید و در شهری بسر میبرید که یک خرده فروش بین المللی در حال برنامه ریزی برای ساخت یک ابرفروشگاه جدید است. کارزاری محلی هم شکل گرفته است که مدعی است اینکار خرده فروشان مستقل کوچک را از بازار بیرون خواهد کرد و بنابراین انتخاب مصرف کننده را کاهش داده و شخصیت محل را تغییر خواهد داد. در مقابل حامیان این طرح استدلال میکنند که این اتفاق تنها زمانی رخ خواهد داد که مصرفکنندگان ابرفروشگاه را ترجیح دهند.
شما کدام طرف هستید؟
پرسش ۷.۱۶ (همه پاسخهای صحیحی را انتخاب کنید)
فرض کنید که در یک شهر کوچک یک خردهفروشِ چندملیتی قصد دارد ابرفروشگاه جدید تأسیس کند. کدامیک از استدلالهای زیر صحیح است؟
- (الف) موجود بودن یک جایگزینِ نزدیک به معنای تقاضای کشسان برای این کالاها است.
- (ب) قابلیت جایگزینی میان کالاها به معنای رقابت میان ارائهدهندگان است که عموماً به قیمت پائینتر میانجامد.
- (ج) اگر خردهفروشان محلی بیرون گذاشته شوند، شرکت چندملیتی از قدرت بازار بیشتری برخوردار خواهد شد. با تقاضای کمتر کشسانی روبهرو خواهد شد، و قادر خواهد بود قیمتها را بدون از دست دادن مشتری بالا ببرد.
- (د) تمایزپذیری زیاد (یعنی قابلیت جایگزینی کم) به معنای تقاضای کمتر کشسان است.
۷.۱۱ انتخاب محصول، نوآوری، و تبلیغات
سودی که یک بنگاه اقتصادی میتواند بدست آورد تابع منحنی تقاضای محصول آن است، که آن هم بهنوبه خود به ترجیحات مصرفکنندگان و رقابت دیگر بنگاههای اقتصادی بستگی دارد. اما ممکن است که بنگاه اقتصادی بتواند منحنی تقاضا را بنحوی جابجا کند که سود خود را بواسطه تغییر در انتخاب محصولات خود، یا بوسیله تبلیغات، افزایش دهد.9
کمپانی برادران پارکر یک بازی رومیزی با مضمون تجارت دارایی به نام مونوپولی را در سال ۱۹۳۵ وارد بازار کرد. برادران پارکر طی مجموعهای از دادگاهها در دهه ۱۹۷۰ میلادی تلاش میکردند تا جلوی رالف آنسپاخ، یک پروفسور رشته اقتصاد که بازیای بنام آنتی-مونوپولی را میفروخت بگیرند. انسپاخ مدعی بود که برادران پارکر ازآنجاکه در اصل مونوپولی را ابداع نکردهاند حق انحصاری فروش آن را ندارند.
وقتی که دادگاه به نفع آنسپاخ رأی داد، نسخههای رقیب دیگری از بازی مونوپولی به بازار آمد.
اما در سال ۱۹۸۴ و در پی تغییر قانون، برادران پارکر انحصار علامت تجاری مونوپولی را بدست آوردند و بهاین ترتیب مونوپولی اکنون دوباره یک انحصار محسوب میشود.
هنگامی که قرار است بر سر نوع کالاهای تولیدی تصمیم گرفته شود، بنگاه اقتصادی به صورت ایده آل تلاش خواهد کرد تا محصولی را پیدا کند که هم برای مصرف کننده جذاب باشد و هم مشخصاتی متمایز از محصولات سایر بنگاههای اقتصادی داشته باشد. در این حالت، تقاضا بالا خواهد بود (بسیاری از مصرفکنندگان تمایل خواهند داشت که آن را در هر قیمتی بخرند) و کشسانی پایین خواهد بود. البته این وضعیت ساده و راحتی نیست: بنگاه اقتصادیی که میخواهد نوع جدیدی از غله صبحانه یا نوع جدیدی از ماشین بسازد، میداند که پیشاپیش برندهای مختلفی در بازار وجود دارند. اما نوآوری فناورانه میتواند فرصتهایی برای جلوتر زدن از رقبا فراهم بیاورد. تا قبل از اینکه تویوتا اولین اتومبیل هیبریدی تولید انبوه خود، یعنی پریوس را در سال ۱۹۹۷ بسازد، تعداد بسیار کمی از اتومبیلهای مشابه آن در بازار وجود داشت. تویوتا بهشکل موثری بازار هیبریدی را در دست گرفت. تا سال ۲۰۱۳ چندین برند رقیب هم بهوجود آمده بود، اما پریوس همچنان پیشتاز بازار باقی ماند که بیش از ۵۰ درصد فروش هیبریدی را در اختیار داشت.
اگر بنگاه اقتصادیی محصول جدیدی را ابداع یا خلق کرده است میتواند با استفاده از حق امتیاز انحصاری و کپی رایت، حق تولید انحصاری آن را مدعی شود و به این ترتیب، کاملاً جلوی رقابت را بگیرد. جالب است که در دهه ۱۹۷۰ شرکتی بهنام پارکِر برادرز سالها وقت خود را صرف جنگیدن در دادگاه کرد تا از حق انحصار خود بر یک بازی رومیزی پرسود بهنام مونوپولی (Monopoly) بدست بیاورد. این نوع حمایت قانونی از مونوپولی ممکن است که مشوقهایی برای طراحی و ساخت محصولات جدید باشد، اما درعین حال عواید ناشی از تجارت را محدود میکند. در فصل ۲۰ مسأله حقوق مالکیت معنوی را با جزئیات بیشتری بررسی خواهیم کرد.
تبلیغات راهبرد دیگری است که با استفاده از آن بنگاههای اقتصادی میتوانند بر تقاضا تأثیر بگذارند: هم تولیدکنندگان اتومبیل و هم تولیدکنندگان غله صبحانه در سطح وسیعی از آن استفاده میکنند. وقتی محصولات متمایز باشند، بنگاه اقتصادی میتواند از تبلیغات مشتریان را از وجود و ویژگیهای محصول خود باخبر کنند، توجه آنها را از کالاهای رقیب به کالای خود جلب کنند، و در مشتریان وفاداری به برند را ایجاد کنند.
براساس نظر شونفلد و همکاران، که بنگاه اقتصادیی از تحلیل گران بازار است، تبلیغات برای غله صبحانه در ایالات متحده حدود ۵.۵ درصد کل درآمدهای فروش است – یعنی حدود ۳.۵ برابر بالاتر از میانگین محصولات تولیدشده. دادههای مندرج در جدول ۷.۲۰ مربوط به ۳۵ برند پرفروش غله صبحانه در ناحیه شیکاگو در سالهای ۱۹۹۱ و ۱۹۹۲ است. نمودار، رابطه میان سهم بازار و هزینهکرد فصلی برای تبلیغات را نشان میدهد. اگر بازار غله صبحانه را با دقت بیشتری بررسی میکردیم، میدیدیم که سهم بازار رابطه نزدیکی با قیمت ندارد. اما همانطور که دادههای شکل ۷.۲۰ نشان میدهند، برندهایی که بیشترین سهم بازار را دارند، بنگاههای اقتصادیی هستند که بیشترین هزینهکرد تبلیغاتی را هم دارند. متیو شوم اقتصاددان، با استفاده از این مجموعه داده خرید غلات در شیکاگو را بررسی کرد و نشان داد که تأثیر تبلیغات در برانگیختن تقاضا برای یک برند موثرتر از تخفیفهای قیمتی است. ازآنجاکه مشهورترین برندها همانهایی هستند که بیشترین هزینهکرد را برای تبلیغات هم دارند، او نتیجه گرفت که کارکرد تبلیغات، اطلاعرسانی به مشتریان درباره محصول نیست، بلکه افزایش وفاداری به برند و جلب مصرفکنندگان سایر برندهای غلات به خود است.10
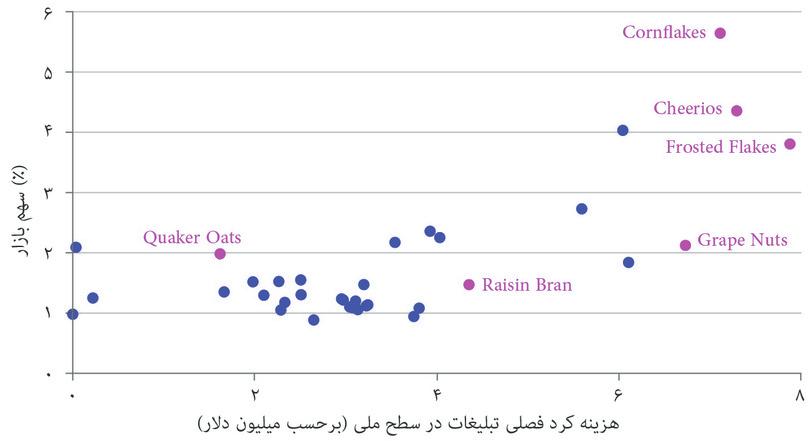
شکل ۷.۲۱ هزینه کرد تبلیغاتی و سهم بازار غله صبحانه در شیکاگو (۱۹۹۲-۱۹۹۱)
Figure 1 in Matthew Shum. 2004. ‘Does Advertising Overcome Brand Loyalty? Evidence from the Breakfast-Cereals Market’. Journal of Economics & Management Strategy 13 (2): pp. 241–72.
۷.۱۲ قیمتها، هزینهها و شکست بازار
شکست بازار هنگامی اتفاق میافتد که تخصیص بازاری یک کالا فاقد کارایی پارتویی باشد، و در این فصل دیدیم که یکی از دلایل شکست بازار (دلایل دیگر را در فصلهای بعدی خواهیم دید) این است که بنگاههای اقتصادی قیمتهایی بالاتر از هزینه نهایی تولید محصولشان تعیین میکنند.
بنگاههای اقتصادی، هنگامی که محصولشان مثلاً اتومبیل یا غله متمایز از محصول کارخانههای دیگر است، قیمت را بالاتر از هزینه نهایی تعیین میکنند تا با این کار بتوانند هم مشتریانی با ترجیحات مختلف را نگه دارند و هم با رقابت محدود مواجه شوند (یا در مورد تولید انحصاری یک کالای بیمشابه، هیچ رقابتی). بنگاههای اقتصادی میتوانند از راهبردهای کاهش رقابت استفاده کنند، اما بدون رقابت هم زیان ثابت میتواند بسیار زیاد باشد و به همین دلیل است که سیاستگذارن تلاش میکنند که این زیان را از طریق خط مشیهای رقابتی کاهش دهند.
تمایز محصول تنها علت قیمت بالاتر از هزینه نهایی نیست. دومین دلیل مهم کاستن از میانگین هزینه است که احتمالاً میتواند بدلیل صرفه جویی ناشی از مقیاس در مرحله تولید، هزینههای ثابت، و یا کاهش قیمت ورودیها با افزایش تعداد خرید بنگاه اقتصادی باشد. در چنین مواردی، میانگین هزینه تولید بزرگتر از هزینه نهایی هر واحد است و منحنی میانگین هزینه شیب رو به پایین دارد. قیمت بنگاه اقتصادی باید حداقل برابر با میانگین هزینه باشد – در غیر اینصورت زیان دهی خواهد داشت. و این بدان معناست که قیمت باید بالاتر از هزینه نهایی باشد.
- انحصارِ طبیعی
- فرآیندِ تولیدی که در آن منحنی میانگینِ هزینهی درازمدت آنقدر شیبِ کاهشی دارد که حفظِ رقابت میانِ شرکتها در این بازار را ناممکن میکند.
البته کاهش دادن میانگین هزینه بهاین معناست که بنگاه اقتصادی وقتی در مقیاس کلان تولید میکند میتواند با هزینه واحد کمتری تولید کند. در تأسیسات داخلی مثل آب و برق و گاز، صرفنظر از تعداد تقاضای مشتری، هزینههای ثابتِ بالایی برای آمادهسازی شبکه وجود دارد. تأسیسات نوعاً بازگشت به مقیاسِ افزایشی دارد. میانگین هزینه تولید یک واحد آب، برق یا گاز هزینه بسیار بالایی خواهد بود مگر اینکه بنگاه اقتصادی در مقیاس کلان کار کند. اگر یک بنگاه اقتصادی واحد میتواند با میانگین هزینه پایینتری نسبت به دو بنگاه اقتصادی مجزا بازار را تأمین کند، اصطلاحاً گفته میشود که این فعالیت صنعتی در حالت انحصار طبیعیقرار دارد.
در حالت انحصار طبیعی، احتمالاً سیاستگذاران نمیتوانند با تشویق رقابت بنگاههای اقتصادی را وادار به کاهش قیمتهایشان کنند، زیرا وقتی بنگاههای اقتصادی بیشتری در بازار باشند، میانگین هزینه بالاتر خواهد رفت. احتمالاً تصمیم خواهند گرفت بجای اینکار، فعالیتهای بنگاه اقتصادی را ساماندهی کنند و اعمال نظر بنگاه اقتصادی را در قیمتها با هدف افزایش مازاد مصرف کننده محدود کنند. یک راه حل جایگزین هم مالکیت عمومی است. اکثر کمپانیهای آبرسانی در سرتاسر جهان در مالکیت بخش عمومی هستند، اگرچه در انگلستان و ولز درسال ۱۹۸۹، و در شیلی در دهه ۱۹۹۰، کل صنعت آب خصوصی شد و تحت نظارت یک آژانس بخش عمومی فعالیت میکند.
مثالی از نوعی دیگر یک کمپانی تولید فیلم است. کمپانی خرج زیادی برای استخدام بازیگر، تکنیسین فیلمبرداری، کارگردان، خرید حق فیلمنامه و تبلیغات شرکت میکند. اینها هزینههای ثابت محسوب میشوند (که گاهی به آنها هزینههای نسخه اول هم گفته میشود). هزینه آماده کردن نسخههای بعدی از فیلم (هزینه نهایی) نوعاً هزینه کمی است: تکثیر نسخه اصلی کار ارزانی است. هزینه نهایی بنگاه اقتصادی پایینتر از میانگین هزینه آن (و منجمله نرخ سود نرمال) خواهد بود. اگر قرار بود قیمتی برابر با هزینه نهایی تعیین کند، ورشکست میشد.
قیمت یک کالای متمایز از هزینه نهایی بالاتر است که این نتیجه پاسخ بنگاه اقتصادی به نبودِ بنگاههای اقتصادی رقیب و عدم حساسیت به قیمت از جانب مشتریان است. خاستگاه مسأله در مورد شرکت تأسیسات و فیلم، ساختار هزینه است، و نبودِ رقیب به خودی خود. برق یک کالای متمایز نیست، و بنابراین خریداران برق ممکن است شدیداً حساس به قیمت باشند، و شرکت فیلم شدیداً رقابتی است. اما برای بقای بنگاههای اقتصادی قیمت همواره باید بالاتر از هزینه نهایی باشد.
با این حال، این دو مسأله – رقابت محدود و میانگین هزینه کاهشی – غالباً پیوند نزدیکی با هم دارند، چراکه رقابت میان بنگاههای اقتصادیی که منحنی میانگین هزینه با شیب رو به پایین دارند، بهتدریج به یک بازی برنده-همه چیز-را-میبرد تبدیل میشود. بنگاه اقتصادی اول برای بهره کشی از مزایای هزینهای ناشی از مقیاس کلان دیگر رقبا را حذف میکند و در نتیجه رقابت را حذف میکند.
قیمت پایینتر از هزینه نهایی، بههرحال و صرف نظر از دلیل آن، سبب شکست بازار میشود. خرید بسیار کمی انجام میشود: خریداران بالقوهای هستند که تمایل به پرداخت آنها بالاتر از هزینه نهایی اما کمتر از قیمت بازار است – اینها خرید نخواهند کرد و بنابراین با یک زیان ثابت روبهرو هستیم.
۷.۱۳ نتیجهگیری
ما بررسی کردیم که بنگاههای اقتصادیی که کالاهای متمایزی تولید میکنند، چگونه قیمت و تعداد خروجی خود بهمنظور حداکثرسازی سود تعیین میکنند. این تصمیمات به منحنی تقاضای محصول – و خصوصاً کشسانی تقاضا – و ساختار هزینه لازم برای تولید آن بستگی دارد. بنگاههای اقتصادی قیمتی بالای هزینه نهایی تولید انتخاب میکنند – حتی وقتی که رقابت محدود است و کشسانی تقاضا پایین است.
بازگشتهای افزایشی به تولید و دیگر مزایای ناشی از هزینه به نفع بنگاههای اقتصادیی که در مقیاس کلان تولید میکنند و هزینه واحد آنها کمتر است تمام میشود. نوآوری هم میتواند هزینهها را کاهش دهد و بر سود بیفزاید.
وقتی قیمت بازار بالاتر از هزینه نهایی تولید است، شکست بازار رخ میدهد: تخصیص کالا کارایی پارتویی ندارد. بنگاههای اقتصادی از سود اقتصادی برخوردار میشوند، اما مازاد مصرف کننده پایینتر از زمانی خواهد بود که قیمت با هزینه نهایی برابر است، و بنابراین زیان ثابت خواهیم داشت. بهاین علت است که وقتی بنگاههای اقتصادی موقعیت غالب را در بازار پیدا میکنند، سیاست گذاران ممکن است نگران شوند. سیاستگذاران میتوانند از خط مشیهای رقابتی و قانون گذاری بهمنظور محدود کردن اعمال قدرت بازار استفاده کنند.
مفاهیم معرفی شده در فصل ۷
پیش از آنکه به فصل بعد بروید، تعریف زیر را مرور کنید:
۷.۱۴ ارجاعات
-
Ernst F. Schumacher. 1973. Small Is Beautiful: Economics as If People Mattered. New York, NY: HarperCollins. Note: link to first 80 pages only. ↩
-
‘Willingness to Pay for a Flight in Space’. Statista. Updated 20 October 2011. ↩
-
Rajindar K. Koshal and Manjulika Koshal. 1999. ‘Economies of Scale and Scope in Higher Education: A Case of Comprehensive Universities’. Economics of Education Review 18 (2): pp. 269–77. ↩
-
Economies of Scale and Scope. The Economist. Updated 20 October 2008. ↩
-
George J. Stigler. 1987. The Theory of Price. New York, NY: Collier Macmillan. ↩
-
Matthew Harding and Michael Lovenheim. 2013. ‘The Effect of Prices on Nutrition: Comparing the Impact of Product- and Nutrient-Specific Taxes’. SIEPR Discussion Paper No. 13-023. ↩
-
Augustin Cournot and Irving Fischer. 1971. Researches into the Mathematical Principles of the Theory of Wealth. New York, NY: A. M. Kelley. ↩
-
John Vickers. 1996. ‘Market Power and Inefficiency: A Contracts Perspective’. Oxford Review of Economic Policy 12 (4): pp. 11–26. ↩
-
John Kay. ‘The Structure of Strategy’ (reprinted from Business Strategy Review 1993). ↩
-
Matthew Shum. 2004. ‘Does Advertising Overcome Brand Loyalty? Evidence from the Breakfast-Cereals Market’. Journal of Economics & Management Strategy 13 (2): pp. 241–72. ↩