فصل ۳ کمیابی، کار و انتخاب
فهرستها و موضوعات فصلها
چگونه افراد بیشترین توان خود را عملی میکنند، و چگونه بدهبستان (یا هزینهفایدهی) میان عواید و زمان فراغت خود را تنظیم میکنند؟
- تصمیم-سازی تحت شرایط کمیابی، یکی از معضلات عام و شناختهشده است، زیرا ما عمدتاً ابزارهای محدودی برای دستیابی به اهدافمان داریم.
- اقتصاددانان برای الگوسازی این وضعیتها تلاش میکنند، نخست با مشخص کردن کلیه اقدامات مقرون بهصرفه و … سپس با ارزیابی اینکه کدامیک از این اقدامات، با توجه به اهداف، بهترین اقدام محسوب میشود.
- هزینهی فرصت توصیفی است از بدهبستانی که با وجود کمیابی گریزناپذیر است: برآورده کردن بیشتر یک هدف بهمعنای کمتر برآورده کردن سایر اهداف است.
- الگوی تصمیم-سازی در شرایط کمیابی را میتوان به موقعیتهای دیگری هم تعمیم داد: مثلاً اینکه وقتی با ضرورت هزینهفایده کردن میان زمان فراغت بیشتر و درآمد بیشتر روبهرو هستیم، چقدر از زمان خود را به کار کردن اختصاص دهیم.
- این الگو همچنین به ما کمک میکند که تفاوت ساعات کاری مردم در کشورهای مختلف، و همچنین تغییرات زمان کاری در طول تاریخ را توضیح دهیم.
تصور کنید که در نیویورک کار میکنید و شغلی دارید که ساعتی ۱۵ دلار در یک هفتهی کاری ۴۰ ساعته، یعنی مجموعاً ۶۰۰ دلار در هفته، برای شما درآمد دارد. هر هفته ۱۶۸ ساعت است بنابراین با ۴۰ ساعت کار در هفته، ۱۲۸ ساعت زمان فراغت برای همهی فعالیتهای غیرکاریتان، منجمله تفریح و خواب، خواهید داشت.
حالا تصور کنید که به یاری بخت، شغلی با درآمد بسیار بالاتر یعنی ششبرابر درآمد قبلی به شما پیشنهاد میشود. دستمزد ساعتی شما در شغل جدید ۹۰ دلار است. علاوه براین، کارفرمایتان به شما اجازه میدهد که تعداد ساعت کاریتان در هفته را نیز تعیین کنید.
آیا باز هم ۴۰ ساعت در هفته کار خواهید کرد؟ اگر اینکار را بکنید درآمدتان شش برابر بیشتر از قبل خواهد بود: یعنی ۳۶۰۰ دلار. یا اینکه تصمیم خواهید گرفت که به همان میزان کالایی که میتوانید با همان درآمد هفتگی ۶۰۰ دلاریتان بخرید راضی باشید؟ حالا در شرایطی هستید که میتوانید همین درآمد را با تقسیم ساعات هفتگی خود به تنها ۶ ساعت و ۴۰ دقیقهی کاری (یعنی یک هفتهی شش روز تعطیل!) بدست بیاورید و حدود ۲۶ درصد زمان فراغت بیشتری نسبت به قبل داشته باشید. یا اینکه از این نرخ دستمزد ساعتی بالاتر استفاده خواهید کرد تا هم درآمد هفتگیتان و هم زمان فراغتتان را، البته به مقدار متوسط، بالا ببرید؟
البته این فکر که یکباره امکان افزایش ششبرابری دستمزد ساعتیتان را پیدا کنید و بتوانید ساعات کاریتان را نیز خودتان انتخاب کنید، احتمالاً چندان واقعگرایانه بنظر نمیرسد. اما براساس مباحث فصل دوم میدانیم که پیشرفت فناوری از انقلاب صنعتی بهاینسو با افزایش چشمگیر درآمدها همراه بوده است. اما حقیقت این است که میانگین درآمد-بر-ساعت واقعی کارگران آمریکایی درطول قرن بیستم واقعاً ششبرابر شده است. و با اینکه کارکنان معمولاً نمیتوانند تعداد ساعت کاری خود در هفته را خودشان به کارفرما اعلام کنند، اما درواقع، والبته در بازههای زمانی طولانی، تعداد ساعت کاری معمول تغییر میکند. تاحدی این پاسخی است به اینکه ما ترجیح میدهیم چقدر کار کنیم. ما در مقام افراد، میتوانیم کاری پارهوقت را انتخاب کنیم، اگرچه این ممکن است گزینههای شغلی ما را محدود کند. احزاب سیاسی نیز به ترجیحات رأیدهندگان واکنش نشان میدهند، و بهاینترتیب در بسیاری از کشورها و بدنبال قوانینی که حداکثر ساعت کار را اجباراً معین میکنند، تعداد ساعت کاری معمول تغییر میکند.
پس باید پرسید که آیا مردم از پیشرفت اقتصادی بهعنوان ابزاری برای مصرف کالای بیشتر استفاده کردهاند یا برای گذراندن اوقات فراغت بیشتر، یا هر دو؟ پاسخ این است: هر دو، اما در کشورهای مختلف به اندازههای متفاوت. بااینکه دریافتی ساعتی در طول قرن بیستم تا بیش از شش برابر برای آمریکاییها افزایش پیدا کرد، اما میانگین زمان کاری سالانه آنها تا کمی بیش از یکسوم کاهش یافت. بهاینترتیب، تا پایان قرن بیستم، مردم شاهد افزایش چهاربرابری درآمد دریافتی سالانهشان بودند که میتوانستند برای خرید کالا و خدمات هزینه کنند، اما درعین حال زمان فراغت شان افزایش بسیار کمتری، یعنی اندکی کمتر از یکپنجم را نشان میداد. (افزایش درصدی زمان فراغت، درصورتی که زمان صرفشده برای خواب بهعنوان زمان فراغت حساب نکنیم، از این هم بیشتر خواهد بود، که البته بازهم نسبت به افزایشی درآمدی ناچیز است). این وضعیت در مقایسه با انتخابتان درخصوص پیشنهادافزایش ششبرابری دستمزد از سوی کارفرمای فرضی، چگونه است؟
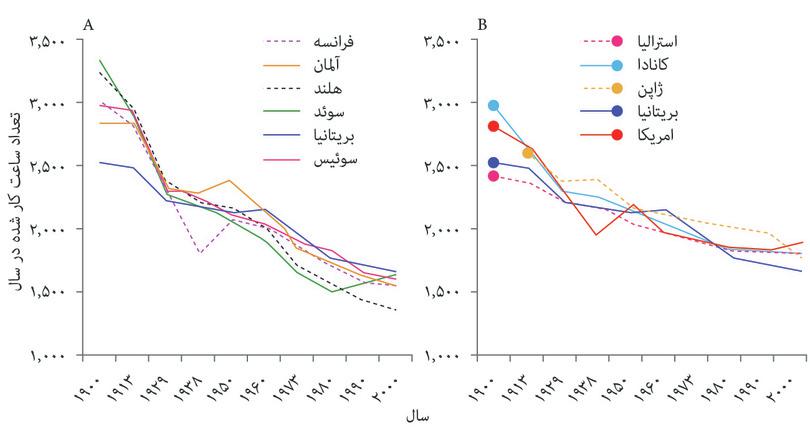
شکل ۳.۱ روندهای مختلف در درآمد و ساعات کاری از سال ۱۸۷۰ در سه کشور مختلف را نشان میدهد.
همانطور که در فصل ۱دیدهایم، درآمد درقالب جی.دی.پی سرانه و به دلار آمریکا محسابه میشود. این با میانگین دریافتی یکی نیست اما بیان مفیدی از درآمد میانگین به منظور مقایسه میان کشورها و زمانهای مختلف به ما میدهد. در اواخر قرن ۱۹ و اوایل قرن ۲۰ میانگین درآمدی تقریباً سه برابر شد و ساعات کار بهشکل چشمگیری کاهش پیدا کرد. در طول باقی سالهای قرن ۲۰ درآمد به ازای هر نفر چهار برابر افزایش پیدا کرد.
ساعات کاری در هلند و فرانسه هم (اگرچه با سرعت کمتر) همچنان کاهش پیدا کرد اما در ایالات متحده، یعنی جایی که از دهه ۱۹۶۰ بهندرت تغییر کرده، به سمت تثبیتشدن حرکت کرد.
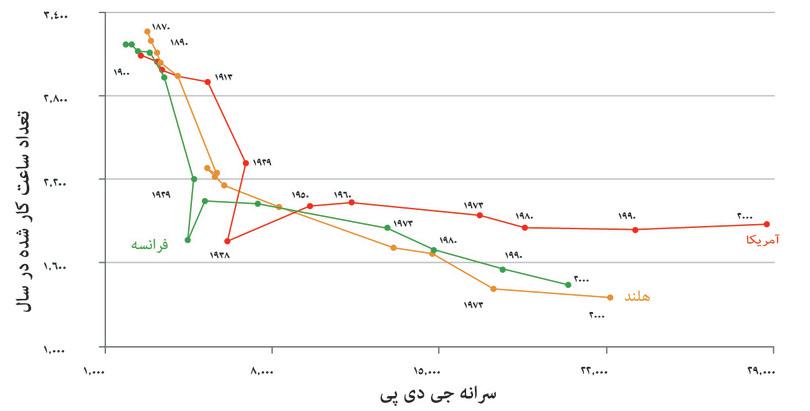
ساعت کار و درآمد سالانه (۱۸۷۰ تا ۲۰۰۰)
شکل ۳.۱ ساعت کار و درآمد سالانه (۱۸۷۰ تا ۲۰۰۰)
Maddison Project. 2013. 2013 edition. Michael Huberman and Chris Minns. 2007. ‘The times they are not changin’: Days and hours of work in Old and New Worlds, 1870–2000’. Explorations in Economic History 44 (4): pp. 538–567. GDP is measured at PPP in 1990 international Geary-Khamis dollars.
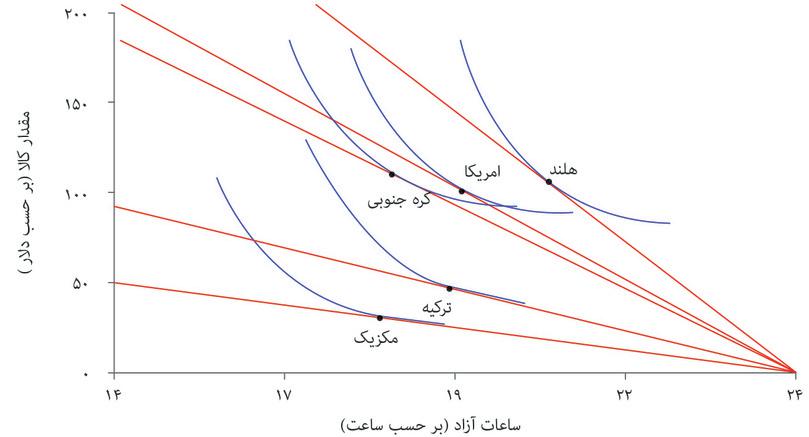
اگرچه بسیاری از کشورها روند مشابهی را طی کردهاند، اما بازهم نتایج حاصله متفاوت بوده است. شکل ۳.۲ ناهمگونیهای گستردهای بلحاظ زمان فراغت و درآمد میان کشورهای مختلف در سال ۲۰۱۳ نشان میدهد. در اینجا ما زمان فراغت را با کسر میانگین سالانه ساعت کاری از تعداد ساعت در هر سال محاسبه کردهایم. ملاحظه میکنید که ظاهراً کشورهای با درآمد بالا ساعات کاری کمتر و زمان فراغت بیشتری دارند، اما تفاوتهای فاحشی هم میان آنها وجود دارد. برای مثال هلند و ایالات متحده سطوح درآمدی مشابهی دارند، اما کارگران هلندی زمان فراغت بسیار بیشتری دارند. یا ایالات متحده و ترکیه زمان فراغت مشابه اما به لحاظ درآمدی تفاوت زیادی دارند.
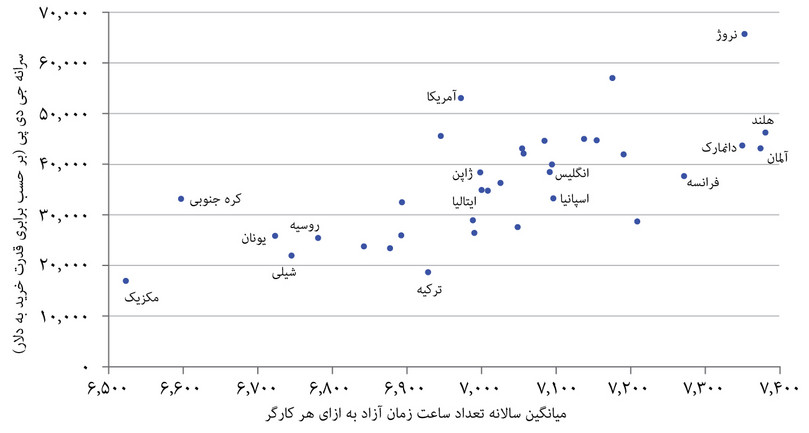
تعداد ساعات زمان فراغت در هفته و درآمد (۲۰۱۳)
شکل ۳.۲ تعداد ساعات زمان فراغت در هفته و درآمد (۲۰۱۳)
OECD. Average annual hours actually worked per worker. OECD. Level of GDP per capita and productivity. Accessed June 2016. Data for South Korea refers to 2012.
در بسیاری از کشورها از دهه ۱۸۷۰ به این سو افزایش خیرهکننده استاندارد زندگی را شاهد بودهایم. اما در برخی کشورها مردم با همان سختکوشی سابق به کار کردن ادامه دادهاند اما درعین حال مصرفشان بیشتر شده، درحالی که در برخی کشورهای دیگر امروزه مردم زمان فراغت بیشتری دارند. چرا چنین اتفاقی افتاده است؟ برای پاسخ دادن به این سوال به یکی از مسائل بنیادی اقتصاد – یعنی کمیابی – خواهیم پرداخت و بررسی خواهیم کرد که در وضعیتی که قدرت دستیابی به همهی چیزهایی که میخواهیم، از کالا تا زمان فراغت، را نداریم، چگونه دست به انتخاب میزنیم.
الگوی تصمیم-گیریای را که دراینجا بکار میگیریم بهدقت بررسی کنید! این الگو در طول این درسها مکرراً مورد استفاده قرار خواهد گرفت، زیرا چشماندازی از طیف گستردهای از مسائل اقتصادی را به ما میدهد.
پرسش ۳.۱ (یک پاسخ را انتخاب کنید)
فرض کنید که در حال حاضر هفتهای ۴۰ ساعت و با نرخ دستمزد ۲۰ پوند در ساعت کار میکنید. تعداد ساعات فراغتِ شما، یعنی تعداد ساعتهایی در هفته که صرف کارکردن نمیشود، عبارت است از ۲۴ ساعت × ۷ روز – ۴۰ ساعت = ۱۲۸ ساعت در هفته. حالا فرض کنید که نرخ دستمزد شما ۲۵ درصد افزایش پیدا کرده است. اگر راضی هستید به اینکه مجموع درآمد هفتگیتان را ثابت نگه دارید، آنگاه:
- (الف) نرخ دستمزد جدید عبارت است از ۲۰ پوند × ۱.۲۵ = ۲۵ پوند در ساعت. درآمد هفتگی قبلی شما عبارت بود از ۲۰ پوند × ۴۰ ساعت = ۸۰۰ پوند. بنابراین مجموع تعداد ساعت کاری جدید شما عبارت است از ۸۰۰ پوند ÷ ۲۵ پوند در ساعت = ۳۲ ساعت. این نشانگر یک تغییر ۲۰- درصدی است: (۴۰-۳۲) ÷ ۴۰ = ۲۰- درصد.
- (ب) نرخ دستمزد جدید عبارت است از ۲۰ پوند × ۱.۲۵ = ۲۵ پوند در ساعت. درآمد هفتگی قبلی شما عبارت بود از ۲۰ پوند × ۴۰ ساعت = ۸۰۰ پوند. بنابراین مجموع تعداد ساعت کاری جدید شما عبارت است از ۸۰۰ پوند ÷ ۲۵ پوند در ساعت = ۳۲ ساعت.
- (ج) نرخ دستمزد جدید عبارت است از ۲۰ پوند × ۱.۲۵ = ۲۵ پوند در ساعت. درآمد هفتگی قبلی شما عبارت بود از ۲۰ پوند × ۴۰ ساعت = ۸۰۰ پوند. بنابراین مجموع تعداد ساعت کاری جدید شما عبارت است از ۸۰۰ پوند ÷ ۲۵ پوند در ساعت = ۳۲ ساعت. پس زمان فراغت شما اکنون عبارت است از ۲۴ ساعت در روز × ۷ روز در هفته – ۳۲ = ۱۳۶ ساعت در هفته، یعنی یک افزایش ۲۵ درصدی به این ترتیب: (۱۲۸-۱۳۶) ÷ ۱۲۸ = ۶.۲۵ درصد ≠ ۲۵ درصد.
- (د) نرخ دستمزد جدید عبارت است از ۲۰ پوند × ۱.۲۵ = ۲۵ پوند در ساعت. درآمد هفتگی قبلی شما عبارت بود از ۲۰ پوند × ۴۰ ساعت = ۸۰۰ پوند. بنابراین مجموع تعداد ساعت کاری جدید شما عبارت است از ۸۰۰ پوند ÷ ۲۵ پوند در ساعت = ۳۲ ساعت. پس زمان فراغت شما اکنون عبارت است از: ۲۴ ساعت در روز × ۷ روز در هفته – ۳۲ = ۱۳۶ ساعت در هفته، یعنی یک افزایش ۶.۲۵ درصدی به این ترتیب: (۱۲۸-۱۳۶) ÷ ۱۲۸ = ۶.۲۵ درصد.
پرسش ۳.۲ (یک پاسخ را انتخاب کنید)
دوباره به شکل ۳.۱ نگاه کنید، که تعداد ساعت کارشده در سال را نسبت به جی.دی.پی سرانه در ایالات متحده، فرانسه و هلند در فاصله سالهای ۱۸۷۰ تا ۲۰۰۰ را نشان میدهد. کدامیک از گزینههای زیر صحیح است؟
- رابطه منفی میان تعداد ساعات کارشده و سرانه جی.دی.پی لزوماً به این معنا نیست که یکی علت دیگری است.
- سرانه جی.دی.پی کمتر در هلند میتواند معلول تعداد عوامل باشد، منجمله این امکان که هلندیها ممکن است درآمد کمتر اما زمان فراغت بیشتری را درنتیجه دلایل فرهنگ و سایر علتها ترجیح دهند.
- سرانه جی.دی.پی فرانسه از حدود ۲۰۰۰ دلار به ۲۰۰۰۰ دلار (یعنی ده برابر) افزایش یافته است درحالی که تعداد ساعات کارشده سالانه از بیش از ۳۰۰۰ ساعت به کمتر از ۱۵۰۰ ساعت کاهش پیدا کرده است.
- بسیار خوب خواهد بود. اما عملکرد گذشته لزوماً به این معنا نیست که همین رویه در آینده هم ادامه پیدا خواهد کرد.
۳.۱ نیروی کار و تولید
در فصل دوم دیدیم که نیروی کار را میتوان بهعنوان یک ورودی در فرآیند تولید کالاها و خدمات در نظر گرفت. نیروی کار (labour) معادل کار (work) است، مثلاً جوشکاری، مونتاژ و تست کردن که از ملزومات تولید یک اتومبیل است. اندازهگیری (سنجش) فعالیت کاری غالباً دشوار است، که همانطور که در فصلهای بعد خواهیم دید نکته مهمی است چراکه کارفرمایان متوجه میشوند که تعیین میزان دقیق کاری که کارکنانشان انجام میدهند غالباً بسیار دشوار است. همچنین ما نمیتوانیم میزان تلاش و کوششی که فعالیتهای مختلف نیاز دارند را بهشکلی مقایسهپذیر (مثلاً پختن یک کیک در برابر ساختن یک اتومبیل) اندازه بگیریم، بنابراین اقتصاددانان غالباً نیروی کار را صرفاً درقالب تعداد ساعت کارشده توسط افراد درگیر در فرآیند تولید میسنجند و اینطور درنظر میگیرند که هرچه تعداد ساعت کارشده افزایش پیدا کند، میزان کالاهای تولیدشده نیز افزایش خواهد یافت.
مثلاً شما بهعنوان دانشجو هر روز یک تصمیم میگیرید: اینکه چه تعداد ساعت را به مطالعه اختصاص دهید. فاکتورهای متعددی ممکن است بر انتخاب شما تأثیر بگذارند: اینکه تاچه حد از کارتان لذت میبرید، اینکه چقدر آن را دشوار میبینید، اینکه دوستانتان چقدر کار میکنند و غیره. احتمالاً بخشی از انگیزه شما برای اختصاص دادن زمان به مطالعه از این باور شما میآید که هرچه زمان بیشتری را به مطالعه اختصاص دهید، به همان میزان هم نمره بیشتری در پایان دوره خواهید گرفت. در این فصل ما الگوی سادهای خواهیم ساخت مبنی بر انتخاب یک دانشجو برای تعیین تعداد ساعتی که میخواهد به کار بپردازد، با این فرض که هرچه زمان بیشتری را به کار اختصاص دهد، نمره نهایی او هم بهتر خواهد بود.
ما رابطه مثبتی را میان تعداد ساعات کاری و نمره نهایی فرض میگیریم، اما آیا هیچ شواهدی برای تأیید این فرض هم وجود دارد؟ گروهی از روانشناسان آموزشی، رفتار مطالعهی ۸۴ دانشجوی دانشگاه دولتی فلوریدا را زیر نظر گرفتند تا عوامل موثر بر عملکرد آنها را شناسایی کنند.1
در نگاه نخست، بنظر میرسد که میان میانگین تعداد ساعتی که هر دانشجو در طول هفته به مطالعه اختصاص میداد و معدل نمرات او در پایان ترم تنها رابطه بسیار ضعیفی وجود داشته باشد. این را در شکل ۳.۳ میبینید.
این ۸۴ دانشجو برحسب تعداد ساعت مطالعهشان به دو گروه تقسیم شدهاند. میانگین معدل برای آن دسته از دانشجویانی که زمان مطالعهی بالایی داشتهاند برابر با ۳.۴۳ است – که تنها کمی بالاتر از معدل آن دستهای است که زمان مطالعهی پایین داشتهاند.
| زمان مطالعه بالا (۴۲ دانشجو) | زمان مطالعه پایین (۴۲ دانشجو) | |
|---|---|---|
| میانگین جی.پی.ای | ۳.۴۳ | ۳.۳۶ |
زمان مطالعه و نمرات
شکل ۳.۳ زمان مطالعه و نمرات
Elizabeth Ashby Plant, Karl Anders Ericsson, Len Hill, and Kia Asberg. 2005. ‘Why study time does not predict grade point average across college students: Implications of deliberate practice for academic performance.’ Contemporary Educational Psychology 30 (1): pp. 96–116. Additional calculations were conducted by Ashby Plant, Florida State University, in June 2015.
اما دقیقتر که نگاه کنیم، متوجه خواهیم شد که این مطالعه نمونه بسیار جذابی است که نشان میدهد چرا در ساختن فرضیات مبتنی بر ثابتبودن سایر شرایط ceteris paribus باید بسیار محتاط بود. در هر گروه ۴۲ نفره از دانشجویان، برخی تفاوتهای بالقوه مهم وجود دارند. یکی از تفاوتهایی که باید درنظر داشت شرایط محیطی مطالعه افراد است: یک ساعت کار در یک اتاق شلوغ پرسروصدا ممکن است به اندازه یک ساعت کار در کتابخانه مفید نباشد.
همانطور که در شکل ۳.۴ میبینیم دانشجویانی که در محیط نامناسب مطالعه میکنند، احتمال اینکه ساعات طولانیتری مطالعه کنند هم بیشتر است. از این ۴۲ دانشجو، ۳۱ نفر زمان مطالعه بالاتری دارند و در مقابل تنها ۱۱ نفر از این دانشجویان محیط مناسبی برای مطالعه دارند. شاید سایر افرادی که در اطرافشان هستند حواس آنها را پرت کردهاند، بطوری که تمام کردن تکالیفشان زمان بیشتری نسبت به دانشجویانی که در کتابخانه مطالعه کردهاند، برده است.
| زمان مطالعه بالا | زمان مطالعه پایین | |
|---|---|---|
| محیط خوب | ۳.۶۳ (۱۱ دانشجو) | ۳.۴۳ (۳۱ دانشجو) |
| محیط بد | ۳.۳۶ (۳۱ دانشجو) | ۳.۱۷ (۱۱ دانشجو) |
شکل ۳.۴ معدل نمرات در محیطهای مناسب و نامناسب برای مطالعه
Plant et al. ‘Why study time does not predict grade point average across college students’, ibid.
حالا به معدل نمرات در ردیف بالا نگاه کنید: اگر محیط مناسب باشد، دانشجویانی که بیشتر مطالعه کردهاند عملکرد بهتری خواهند داشت – و در ردیف پایین هم میبینید که زمان مطالعه بالا برای کسانی که در محیط نامناسب مطالعه میکنند هم جوابگو بوده است. واضح است که این رابطه، وقتی که محیط مطالعه را در نظر نگرفته بودیم، تااینحد شفاف نبود.
بهاینترتیب روانشناسان، پس از لحاظ کردن محیط و سایر عوامل مربوطه (منجمله معدلهای قبلی دانشجو، و یا تعداد ساعاتی که به کار مزدی یا مهمانی کردن گذراندهاند)، پیشبینی کردند که هر ساعت اضافی در زمان مطالعه هفتگی، معدل دانشجو در پایان ترم را بطور میانگین به اندازه ۰.۲۴ نمره افزایش میدهد. اگر دو دانشجو را که در همه موارد بجز زمان مطالعه شرایط یکسانی دارند درنظر بگیریم، پیشبینی ما این خواهد بود که دانشجویی که زمان بیشتری مطالعه کرده معدلی کسب خواهد کرد که به ازای هر ساعت اضافی مطالعه به اندازه ۰.۲۴ نمره بالاتر است: زمان مطالعه معدل را به ازای هر ساعت به اندازه ۰.۲۴ نمره بالا میبرد، با فرض ثابتبودن سایر شرایط.
تمرین ۳.۱ مفروضات مبتنی بر ثابتبودن سایر شرایط
فرض کنید از شما خواسته شده یک مطالعه تحقیقی درست مشابه تحقیق دانشگاه دولتی فلوریدا در دانشگاهتان انجام دهید.
- بنظر شما برای ساختن الگویی درباب رابطه میان ساعات مطالعه و نمرات نهایی، چه عواملی باید ثابت فرض شوند؟
- علاوه بر محیط مطالعه، احتمالاً به جمعآوری چه اطلاعات دیگری درباره دانشجویان ممکن است نیاز پیدا کنید؟
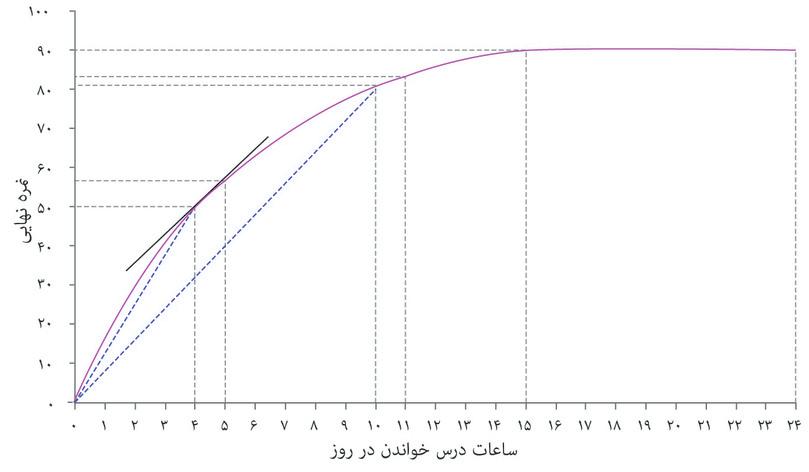
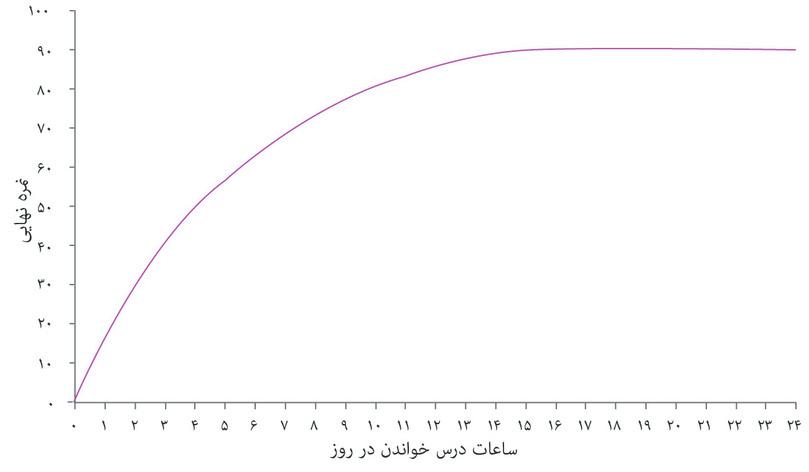
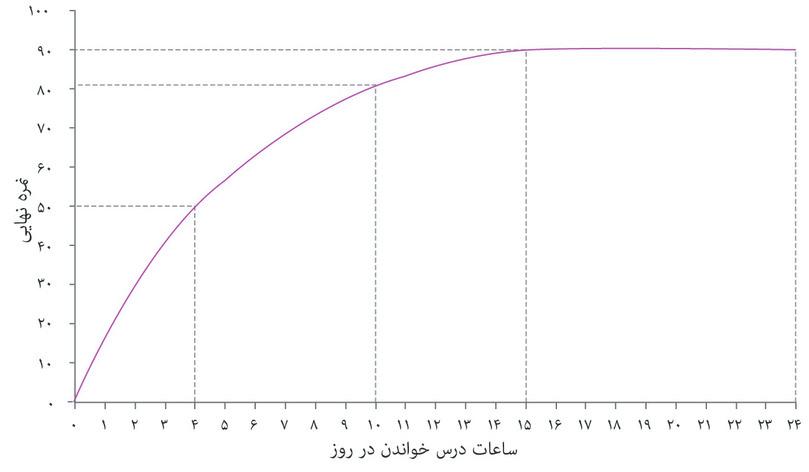
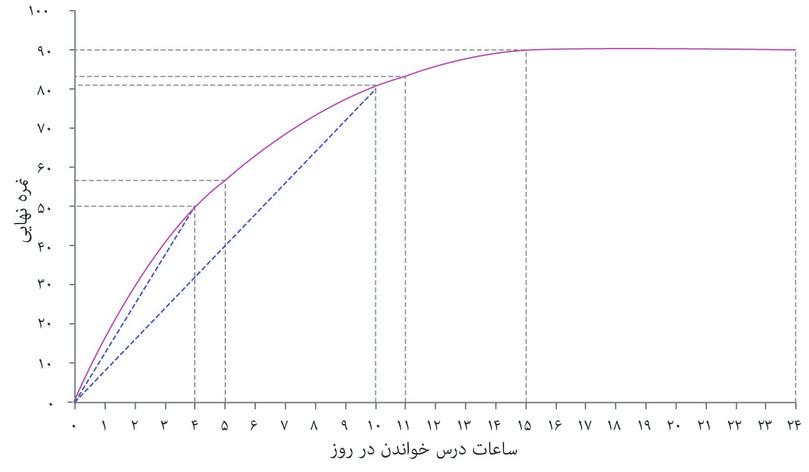
حالا تصور کنید که دانشجویی، که ما او را الکسی مینامیم، میتواند تعداد ساعات مطالعه خود را تغییر دهد. ما فرض خواهیم کرد که درست مثل مورد مطالعه دانشگاه فلوریدا، ساعاتی که او در طول ترم به مطالعه اختصاص میدهد، درصد نمره (رتبه درصدی) که در پایان ترم بدست میآورد را، با فرض ثابت بودن سایر شرایط، افزایش میدهد. این رابطه میان زمان مطالعه و نمره نهایی در جدول مندرج در شکل ۳.۵ نشان داده شده است. در این الگو، زمان مطالعه به همهی زمانی که الکسی به آموختن میگذراند اطلاق میشود، حالا چه در کلاس یا بطور انفرادی، که به ازای هر روز اندازهگیری میشود (و نه مثل مورد دانشجویان فلوریدا به ازای هفته). جدول نحوه تفییرات نمره او همراه با تغییر زمان مطالعه را نشان میدهد، البته اگر همه عوامل دیگر – مثلاً شرایط زندگی اجتماعی او – ثابت فرض شوند.
- تابع تولید
- نوعی بیان تصویری یا ریاضی است که میزانی خروجیِ قابلتولید با هر مقدار یا ترکیبِ معینی از ورودیها میتواند تولید شود. این تابع توصیفی است از فناوریهای مختلفی که قادر به تولید چیز یکسانی هستند.
این تابع تولید الکسی است: تابعی که تعداد ساعت اختصاص یافته به مطالعه در هر روز را (یا بعبارت دیگر کار ورودی او را) به درصد نمره او (یا همان خروجی) تبدیل میکند. درواقع، نمره نهایی از وقایع پیشبینیناپذیر هم متأثر شود (وقایعی که در زندگی روزمره غالباً آنها را یککاسه میکنیم و «شانس» مینامیم). یا میتوانید اینطور در نظر بگیرید که تابع تولید چیزی است که به ما میگوید تحت شرایط نرمال (یعنی نه شانس و نه بدشانسی) الکسی دستاوردی خواهد داشت.
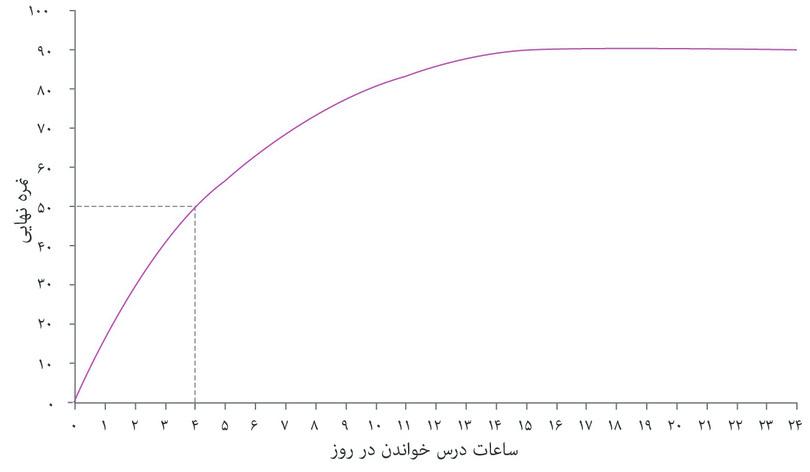
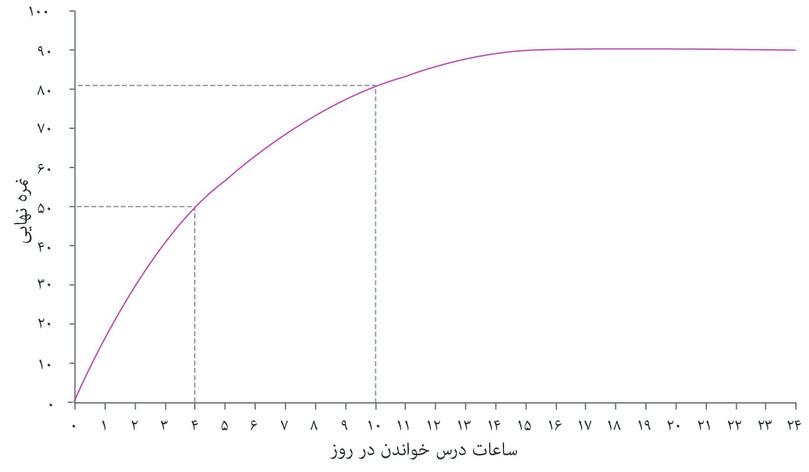
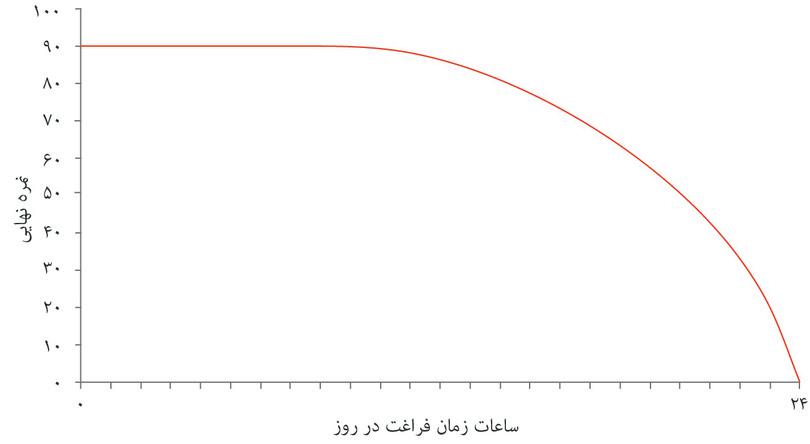
اگر این رابطه را روی یک نمودار ترسیم کنیم به منحنی شکل ۳.۵ میرسیم. الکسی میتواند با مطالعه بیشتر نمره بالاتری هم بگیرد، بنابراین منحنی شیب رو به بالا پیدا میکند. با ۱۵ ساعت مطالعه در روز او به بیشترین نمرهای که توان آن را دارد، یعنی ۹۰ درصد، دست پیدا میکند. و هر مقدار زمانی بیشتر از این حد دیگر تأثیری بر نتیجه امتحان او نخواهد داشت (یعنی آنقدر خسته خواهد بود که مطالعه بیشتر در هر روز دیگر حاصلی نخواهد داشت)، و منحنی تخت میشود.
- میانگین تولید
- کل خروجی تقسیم بر یک ورودی معین، مثلاً به ازای هر کارگر (یعنی تقسیم بر تعداد کارگران) یا به ازای هر کارگر در هر ساعت (یعنی کل خروجی تقسیم بر کل تعداد ساعت کاری صرف شده برای آن).
میتوانیم میانگین تولید نیروی کار الکسی را، درست مثل کشاورزان در فصل دوم، محاسبه کنیم. اگر روزی ۴ ساعت کار کند، نمرهای برابر با ۵۰ بدست میآورد. میانگین محصول– یعنی میانگین تعداد درصد نمرهای که به ازای هر ساعت مطالعه میگیرد – عبارت است از: ۵۰÷ ۴ = ۱۲.۵. این در شکل ۳.۵ معادل شیب شعاعی است که از نقطه شروع به نقطه ۴ ساعت در روز روی منحنی متصل میشود:
- محصول نهایی
- عبارت است از میزانِ خروجیِ مازادی که با افزایش یک واحدیِ یک ورودیِ معین درعین ثابت نگهداشتنِ سایر ورودیها، قابل تولید است.
محصول نهایی عبارت است از افزایش نمرهی حاصل از یک ساعت افزایش در زمان مطالعه. از خطوط جانبی کمک بگیرید تا ببینید که چگونه محصول نهایی را باید محاسبه کرد، و آن را با میانگین محصول مقایسه کنید.
در هر نقطه روی تابع تولید، محصول نهایی عبارت است از افزایش نمرهی ناشی از یک ساعت مطالعه بیشتر. محصول نهایی معادل شیب تابع تولید است.
لایبنیتز: میانگین محصول و محصول نهایی
- کاهشیابنده
- وضعیتی است که در آن استفاده از یک واحدِ اضافی از یکی مولفههای تولید، افزایشِ کوچکتری در خروجی نسبت به افزایشِ قبلی را در پی دارد. همچنان به عنوان روند کاهشی بازگشت نهایی تولید شناخته میشود.
در شکل۳.۵ تابع تولید الکسی، هرچه او ساعات بیشتری مطالعه میکند، تختتر میشود، بنابراین هر چه روی منحنی جلوتر میرویم، محصول نهایی یک ساعت کار اضافی کمتر و کمتر میشود. محصول نهایی کاهشیابندهاست. این الگو بیانی از این ایده است که یک ساعت مطالعه اضافی تنها درحالتی که میزان مطالعه شما زیاد نیست، کمککننده است، اما در صورتی که پیشاپیش مطالعه زیادی دارید، آنگاه دیگر مطالعه اضافی دیگر کمک چندانی نمیکند.
لایبنیتز: محصول نهایی کاهشیابنده
- مقعر
- تابعی است از دو متغیری که برای آنها بخشِ خطیِ میان هر دو نقطه روی تابع، کاملاً زیری منحنیِ نشاندهنده تابع قرار میگیرد (وقتی بخش خطی بالای تابع قرار بگیرد، تابع محدب خواهد بود).
در شکل ۳.۵خروجی همگام با افزایش ورودی افزایش پیدا میکند، اما محصول نهایی کاهش مییابد – تابع تدریجاً تختتر میشود. تابع تولیدی با این شکل را یک تابع تولید مقعر مینامیم.
لایبنیتز: توابع مقعر و محدب
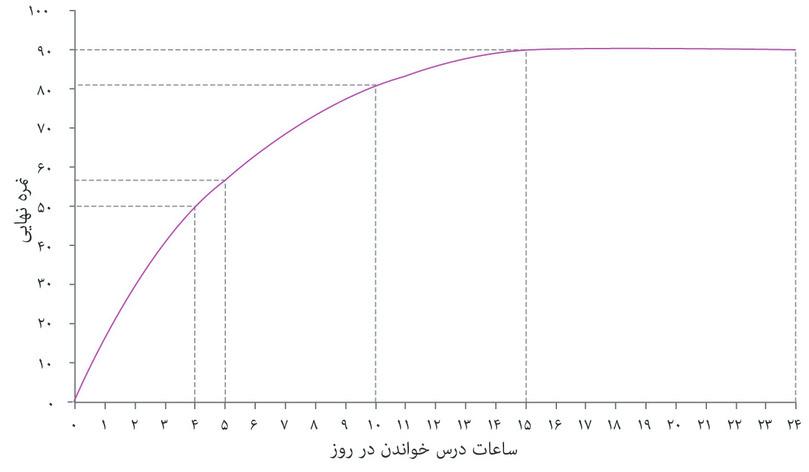
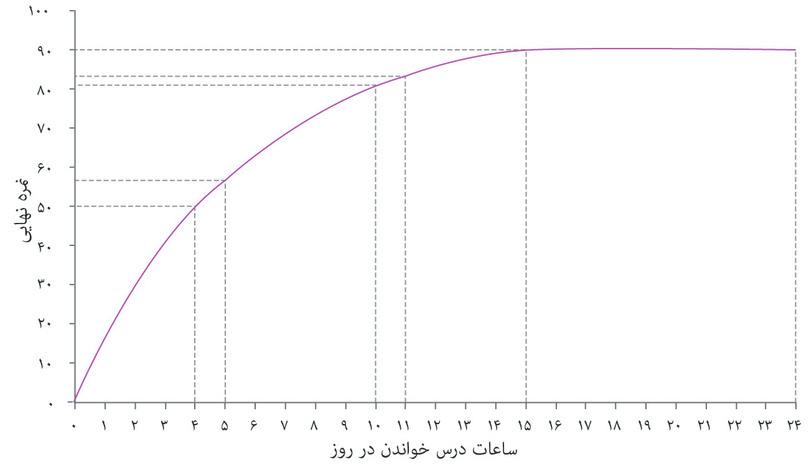
اگر محصول میانگین و محصول نهایی را در هر نقطهای از تابع تولید الکسی مقایسه کنیم، خواهیم دید که محصول نهایی کمتر از میانگین محصول است. برای مثال وقتی الکسی ۴ ساعت کار میکند میانگین تولید او ۵۰ ÷ ۴ = ۱۲.۵ است، اما یک ساعت کار اضافی نمره او را از ۵۰ به ۵۷ میرساند و بنابراین میانگین تولید ۷ است. این به این دلیل است که میانگین تولید خصلت کاهشیابنده دارد: هر ساعت کار نسبت به ساعتهای کاری پیش از خود کمتر مولد است. و این تلویحا به این معناست که میانگین تولید نیز کاهشیابنده است: هر ساعت کار اضافی به ازای هر روز میانگین تولید همه زمان کاری او بهعنوان یک کل را نیز کاهش میدهد.
این نمونه دیگری از میانگین تولید کاهشیابندهی نیروی کار است که در فصل دوم دیدیم. در آن مورد نیز میانگین تولید نیروی کار در تولید غذا (میزان غذای تولیدشده به ازای هر کارگر)، هرچه کارگران بیشتری روی یک مساحت معین زمین کار میکردند، کاهش مییافت.
نهایتاً اینکه توجه داشته باشید که اگر الکسی از همان ابتدا ۱۵ ساعت در روز کار میکرد، محصول نهایی هر ساعت کار اضافی صفر میبود؛ یعنی مطالعه بیشتر نمره او را افزایش نخواهد داد. احتمالاً براساس تجربه شخصیتان هم این را میدانید که کمبود خواب یا زمان استراحت هم میتواند نمره الکسی درصورتی که بیش از ۱۵ ساعت در روز کار کند، بازهم کاهش دهد. اگر اینطور باشد تابع تولید او بازهم شیب بیشتری رو بهپایین پیدا خواهد کرد و محصول نهایی الکسی منفی خواهد شد.
- شیب خط مماس
- No definition available.
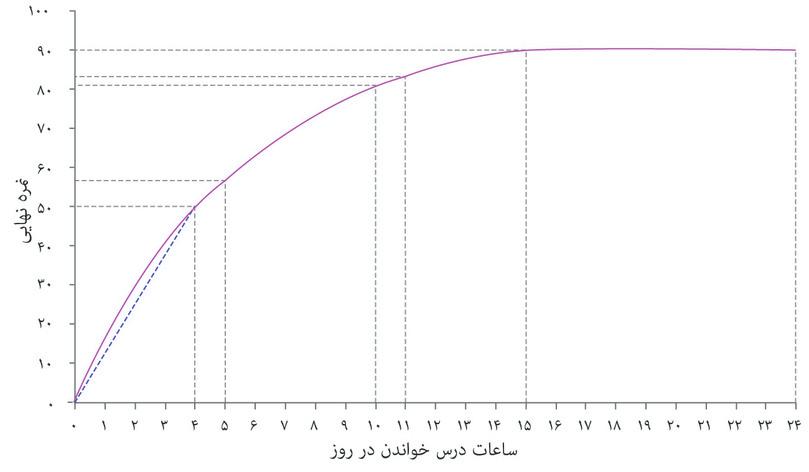
تغییر نهایی مفهوم مهم و عامی در علم اقتصاد است. اغلب آن را بصورت نوعی شیب روی نمودار خواهید دید. اگر تابع تولید مثل مورد شکل ۳.۵ باشد، با جلورفتن روی منحنی، شیب هم بطور پیوسته تغییر خواهد کرد. گفتیم که وقتی الکسی ۴ ساعت در روز مطالعه کند، محصول نهایی او برابر ۷ خواهد بود، که معادل میزان افزایش نمره ناشی از یک ساعت مطالعه اضافی است. از آنجا که شیب منحنی بین ۴ و ۵ ساعت روی محور افقی تغییر میکند، این تنها تخمینی از محصول نهایی واقعی خواهد بود. به عبارت دقیقتر، محصول نهایی عبارت است از نرخ افزایش نمره به ازای هر ساعت کار اضافی. در شکل ۳.۵ محصول نهایی واقعی، شیبِ خط مماس بر منحنی در نقطه ۴ ساعت است. در این فصل ما به دفعات از تخمینهای اینچنینی استفاده خواهیم کرد تا بتوانیم با اعداد رُند کار کنیم، اما بهتر است توجه داشته باشید که گاهی این اعداد دقیقاً و کاملاً با شیب واقعی برابر نیستند.
تمرین ۳.۲ توابع تولید
- نموداری رسم کنید برای نشان دادن تابع تولیدی که، برخلاف مورد الکسی، با افزایش ورودی شیب رو بهپایین پیدا کند.
- آیا میتوانید فرآیند تولیدی را تصور کنید که چنین شکلی داشته باشد؟ چرا شیب روند رو بهپایین پیدا میکند؟
- درباره محصول نهایی و محصول میانگین در این مورد چه میتوانید بگویید؟
محصول نهایی
محصول نهایی نرخ تغییر نمره در نقطه ۴ ساعت مطالعه است. تصور کنید که الکسی ۴ ساعت در روز کار میکرده و حالا هر روز ۱ دقیقه بیشتر از قبل کار میکند (یعنی مجموعاً ۴.۰۱۶۶۶۷ ساعت). بنابراین براساس نمودار، نمره او به اندازهی بسیار کمی بالا خواهد رفت – یعنی حدود ۰.۱۲۴ نمره). براورد دقیقتری از محصول نهایی (یا نرخ تغییرات) به این شکل خواهد بود:
اگر تغییرات جزئی در زمان مطالعه را بازهم بیشتر مورد دقت قرار دهیم (مثلاً افزایش نمره به ازای هر ثانیه اضافی مطالعه در روز) بازهم به محصول نهایی یا همان شیب خط مماس بر منحنی در نقطه ۴ ساعت مطالعه روزانه، نزدیکتر خواهیم شد.
پرسش ۳.۳ (یک پاسخ را انتخاب کنید)
شکل ۳.۵ تابع تولید الکسی را نشان میدهد، که در آن نمره نهایی (خروجی) انعکاسی از تعداد ساعات صرفشده برای مطالعه (ورودی) است.
کدامیک از گزینههای زیر صحیح است:
- (الف) ازآنجا که پیش از این هیچ ساعت قبلیای برای لحاظ کردن نداریم، میانگین تولید برای نخستین ساعت صرفاً همان پیشرفتی است که ظرف و درطول همان یک ساعت تولید شده است، که این به نوبه خود تقریباً معادلِ محصول نهایی در فاصله صفر تا ۱ ساعت است (میزان دقیق محصول نهایی در طول این فاصله تغییر میکند، که خود را در شیب کاهشیابنده تابع تولید نشان میدهد).
- (ب) تولید نهایی در نقاط پس از ۱۵ ساعت ثابت است، اما میانگین تولید همچنان روند کاهشی خود را ادامه میدهد. به این دلیل که محصول نهایی (صفر) کمتر از میانگین تولید است که مثبت باقی میماند اما روندی کاهشی دارد (بعبارت دیگر ساعات اضافی مطالعه که نتیجهای در برندارد، میانگین را کاهش میدهد).
- (ج) اگ مطالعه بیش از ۱۵ ساعت تأثیری منفی بر نمره الکسی میداشت، آنگاه باید محصول نهایی منفی میبود، که این بمعنای یک منحنی با شیب رو به پائین در نقاط پس از ۱۵ ساعت خواهد بود.
- (د) میانگین تولید در نقطه ۲۰ ساعت برابر با ۹۰ نمره ÷ ۲۰ ساعت = ۴.۵ نمره بهازای هر ساعت است. با این حال، محصول نهایی صفر است – همانطور که میبینید تابع تولید بالای نقطه ۱۵ ساعت تخت است.
۳.۲ ترجیحات
- ترجیحات
- توصیفی است از عواید یا هزینهای که به هریک از نتایج ممکن نسبت میدهیم.
اگر الکسی تابع تولیدی شبیه به شکل ۳.۵ داشته باشد، آنگاه چند ساعت مطالعه در روز را انتخاب خواهد کرد؟ این تصمیم به ترجیحات(یا اولویتهای) او بستگی دارد – یعنی مسائلی که او به آنها اهمیت میدهد. اگر تنها نمره برای او مهم باشد، قاعدتاً باید ۱۵ ساعت در روز مطالعه کند. اما الکسی هم مثل بسیاری از سایر مردم، به زمان آزاد خود هم اهمیت میدهد – دلش میخواهد بخوابد، بیرون برود یا تلویزیون تماشا کند. بنابراین، با یک بدهبستان یا سبک سنگین کردن روبهرو میشود: چند درصد از نمرهاش را حاضر است برای صرف کردن وقتش به اموری غیر از مطالعه ازدست بدهد؟
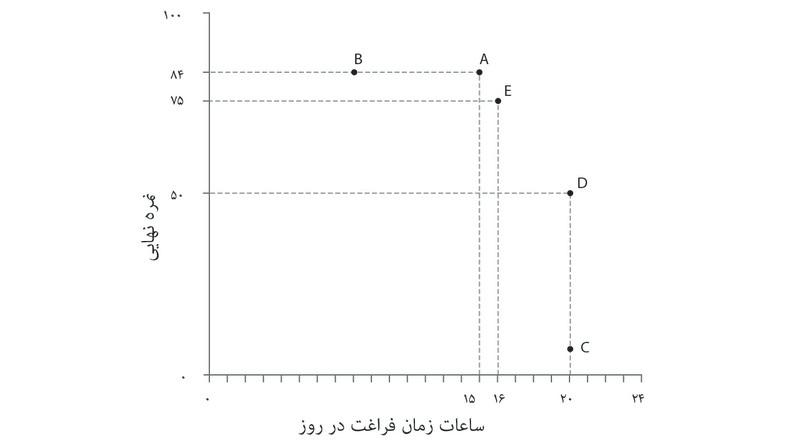
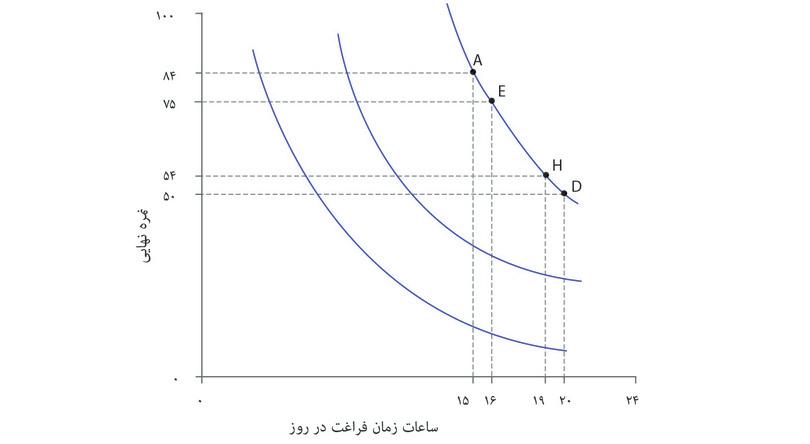
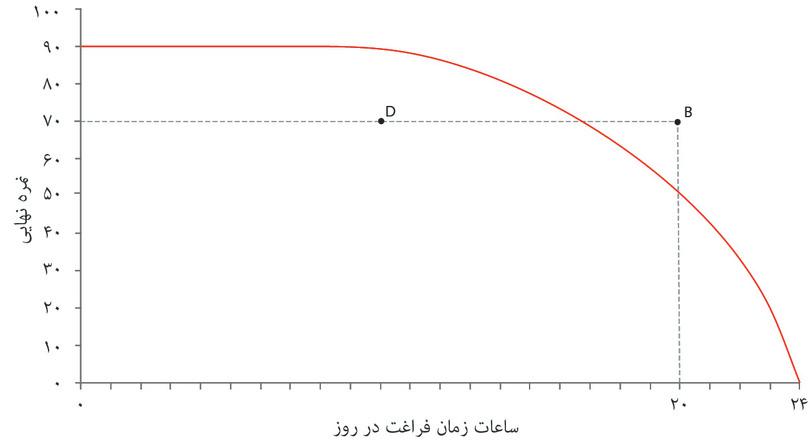
در شکل ۳.۶ ترجیحات یا اولویتهای او را نمایش دادهایم، همراه با زمان فراغت روی محور افقی و نمرات نهایی روی محور عمودی. زمان آزاد یا فراغت به کل زمانی اطلاق میشود که به کاری غیر از مطالعه کردن صرف میشود. هر نقطه روی نمودار نمایانگرترکیب متفاوتی از زمان آزاد و نمره نهایی است. با توجه به تابع تولید الکسی، همه ترکیباتی را که الکسی خواهان آن است ممکن نخواهند بود، اما فعلاً ما ترکیباتی را مدنظر میگیریم که او ترجیحشان میدهد.
میتوانیم درنظر بگیریم که:
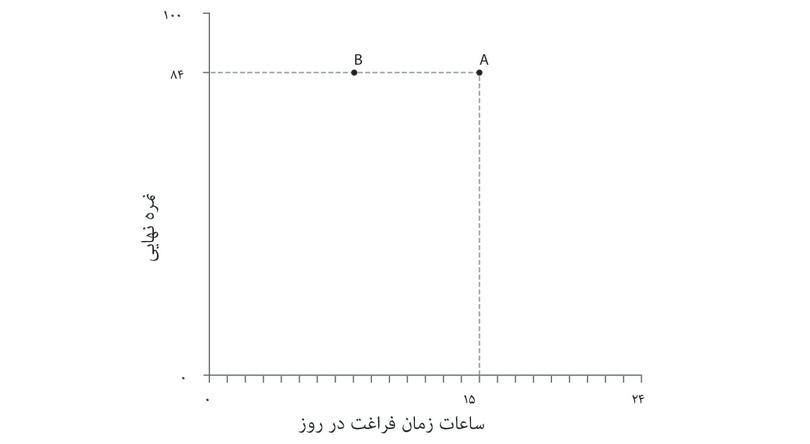
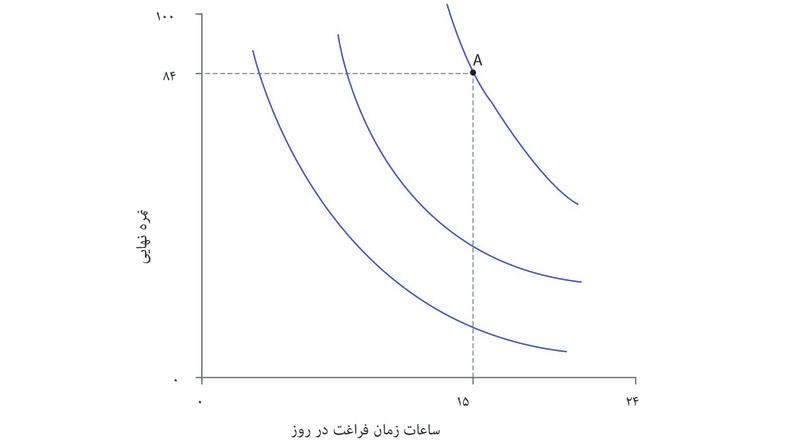
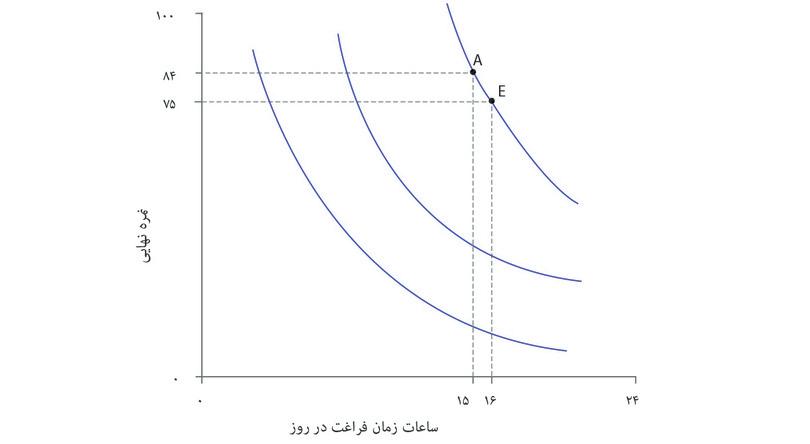
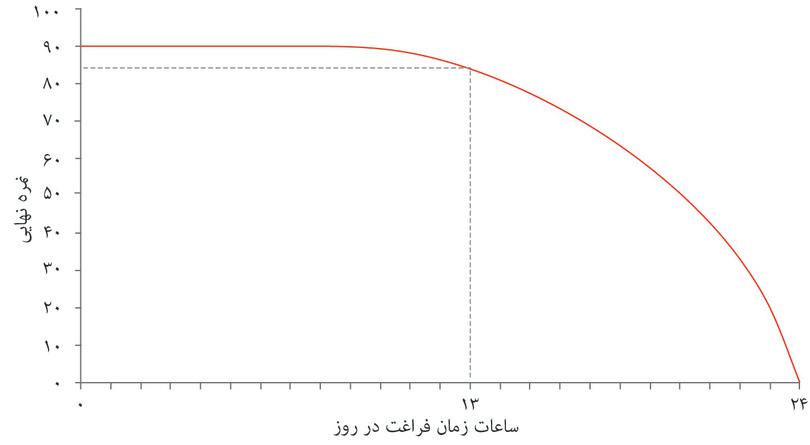
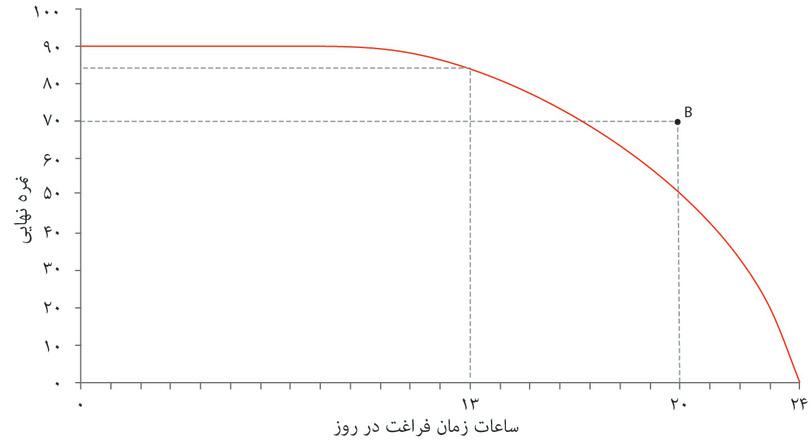
- به ازای هر نمره، الکسی ترکیباتی را که از زمان آزاد بیشتری برخوردارند نسبت به ترکیبات با زمان آزاد کمتر ترجیح میدهد. بنابراین، با اینکه A و B در شکل ۳.۶ هردو به نمره ۸۴ مربوط میشوند، الکسی گزیته A را ترجیح میدهد چون از زمان آزاد بیشتری برخوردار است.
- به همین ترتیب، اگر دو ترکیب هر دو ۲۰ ساعت زمان آزاد دارند، او گزینهای را ترجیح میدهد که نمره بیشتری دارد.
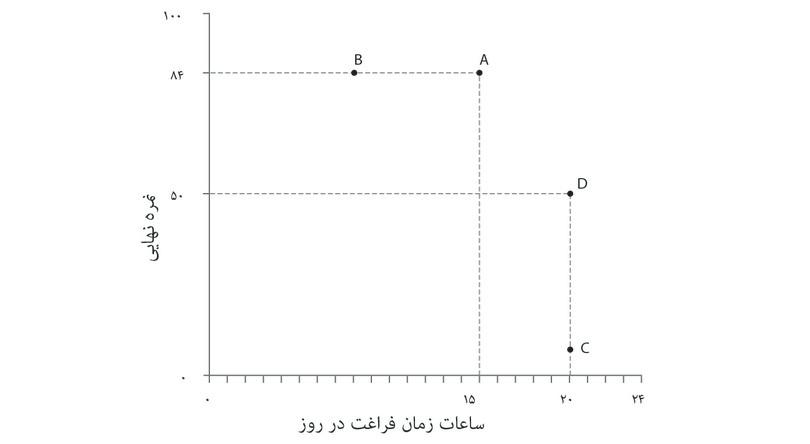
- اما نقاط A و D را در جدول مقایسه کنید. آیا الکسی ترکیب D (نمره پایین و زمان زیاد) را ترجیح میدهد یا ترکیب A (نمره بالاتر و زمان کمتر) را؟ یک راه این است که از خود او سوال کنیم.
- مطلوبیت
- نوعی شاخصِ عددی از ارزشی که فرد برای یک نتیجه قائل میشود، بطوریکه نتایجِ برخوردار از ارزشِ بالاتر بر نتایجِ برخوردار از ارزشِ کمتر، در شرایطی که هر دو مقرون به صرفه هستند، ترجیح داده میشود.
فرض کنید که الکسی میگوید که گزینههای A و D برایش تفاوتی ندارند، به این معنا که هردو نتیجه برای او رضایتبخش خواهند بود. در این حالت میگوییم که هر دو گزینه برای الکسی مطلوبیتیکسانی دارند. ازآنجاکه میدانیم گزینه A را به B ترجیح میدهد، پس B مطلوبیت کمتری نسبت به A و D به همراه دارد.
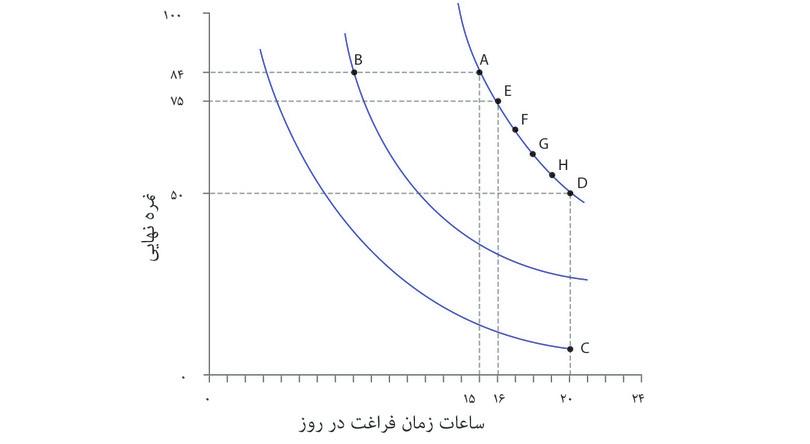
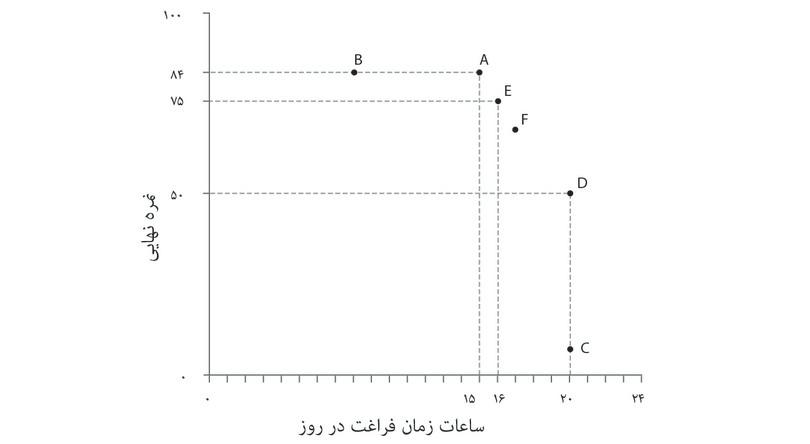
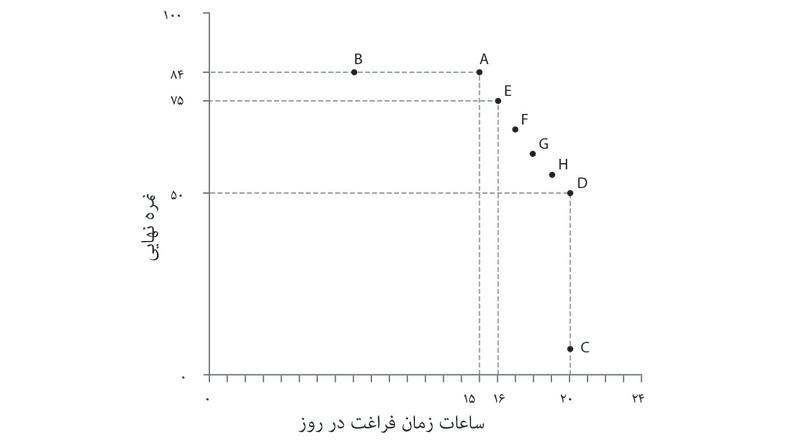
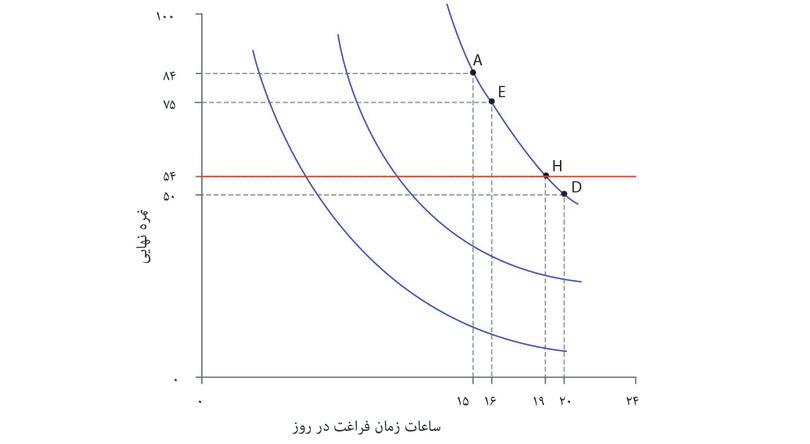
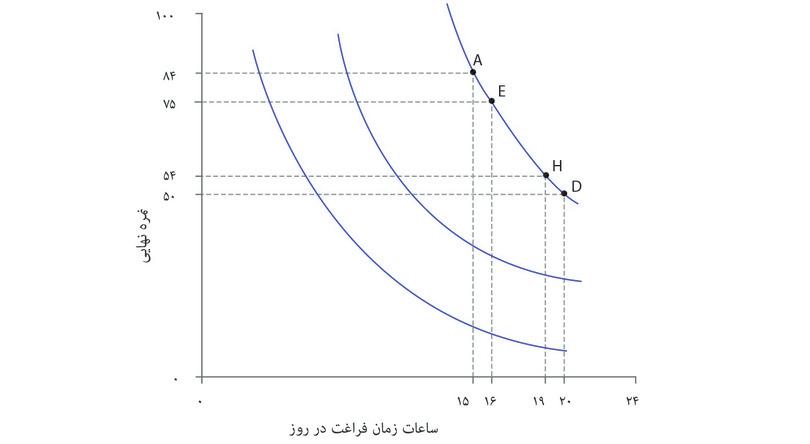
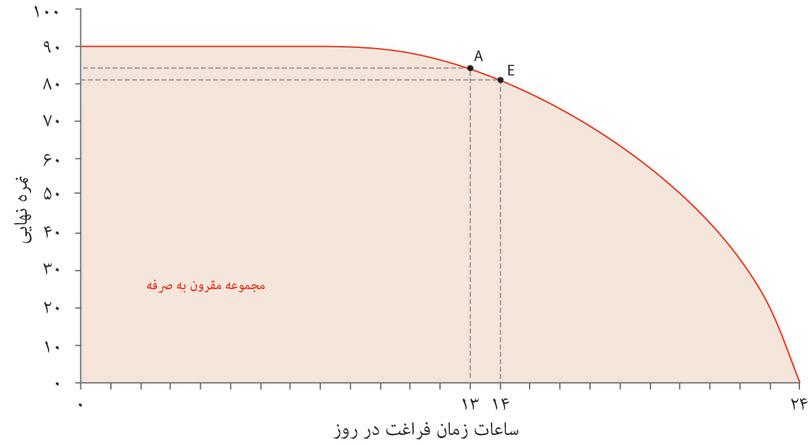
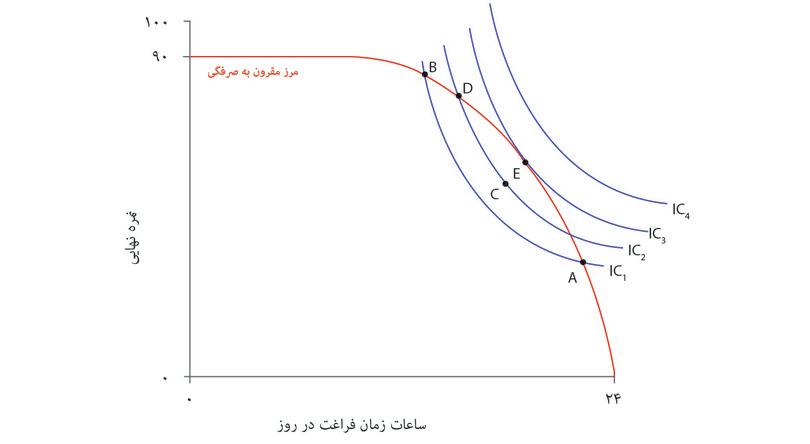
شیوهی نظاممند برای نمایش هندسی ترجیحات الکسی این خواهد بود که بدنبال همه ترکیباتی باشیم که مطلوبیتی برابر با گزینههای A و D به او میدهند. میتوانستیم از الکسی سوال دیگری بپرسیم: «فرض کن که میتوانستی ترکیب نقطه A را داشته باشی (یعنی ۱۵ ساعت زمان آزاد و نمره ۸۴). چند نمره را حاضری برای یک ساعت زمان آزاد بیشتر از دست بدهی؟» و فرض کنید که او پس از بررسی کافی پاسخ بدهد «۹ نمره». آنوقت ما میتوانستیم نتیجه بگیریم که گزینه A و E (۱۶ ساعت و ۷ نمره) برای او فرقی نمیکنند. سپس همین سوال را میتوانیم درباره ترکیب E تکرار کنیم و به همین ترتیب تا نقطه D ادامه دهیم. درنهایت میتوانیم جدولی شبیه جدول موجود در شکل ۳.۶ رسم کنیم. برای الکسی گزینههای A و E علیالسویهاند، و E و F و الی آخر، که به این معناست که همه ترکیبات از A تا D برای او بیتفاوت و علیالسویهاند.
- منحنی بیتفاوتی
- منحنیای متشکل از نقاطی که نشانگرِ ترکیبهای از کالا هستند که سطحِ معینی از مطلوبیت برای فرد را برآورده میکنند.
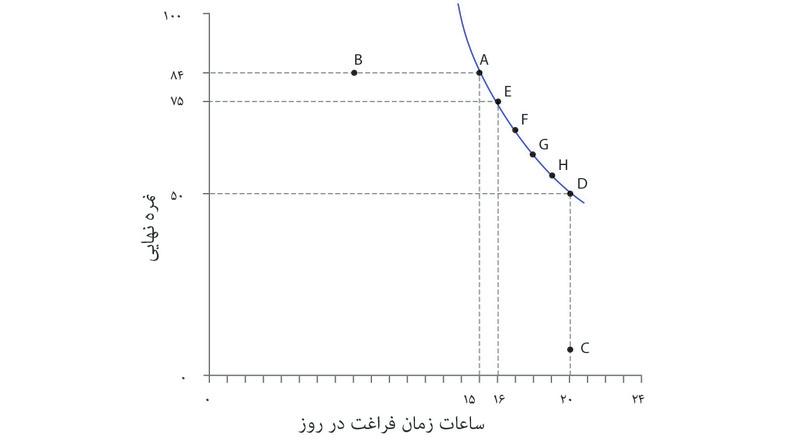
ترکیبات جدول را در قالب شکل ۳.۶ ترسیم و به هم متصل شدهاند تا یک منحنی با شیب-روبهپایین موسوم به منحنی بیتفاوتیرا تشکیل دهند، منحنی که نتیجه اتصال همه ترکیباتی است که مطلوبیت یا «رضایت» یکسانی برای او دارند.
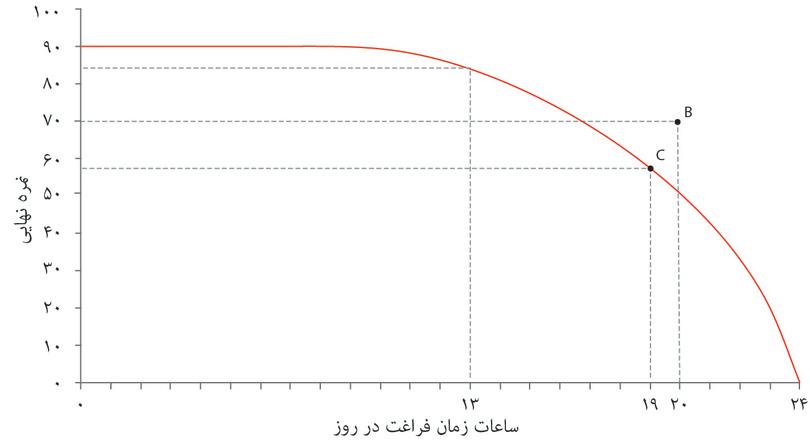
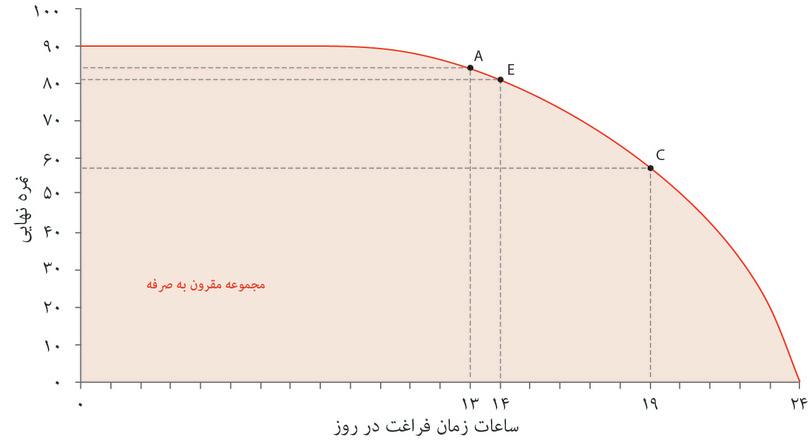
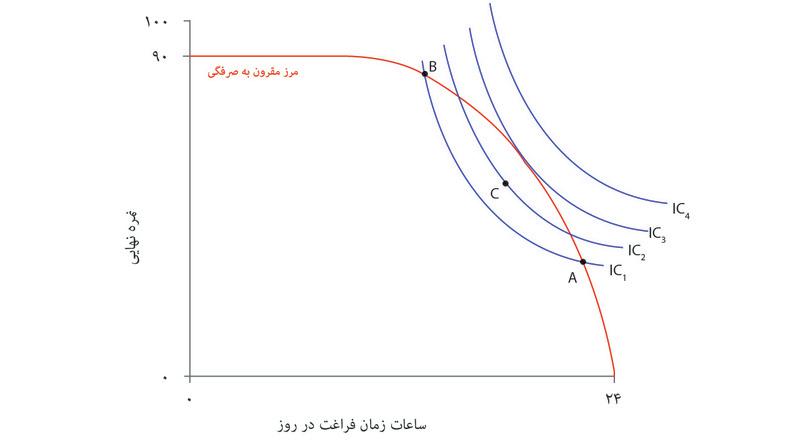
اگر به سه منحنی رسم شده در شکل ۳.۶ توجه کنید، میبینید که منحنی رسمشده از نقطه A مطلوبیت بیشتری نسبت به منحنی رسمشده از نقطه B دارد. و منحنی رسمشده از نقطه C هم کمترین مطلوبیت را در این سه گزینه نشان میدهد. برای تبیین اولویتها یا ترجیحات، نیازی نیست که مطلوبیت دقیق هر گزینه را بدانیم؛ کافی است بدانیم چه گزینههایی نسبت به گزینههای دیگر مطلوبیت کمتر یا بیشتری فراهم میکنند.
- کالاهای مصرفی
- کالا یا خدماتی که نیازهای مصرفکنندگان را در یک بازه زمانی کوتاه برآورده میکند.
منحنیهایی که رسم کردهایم، مفروضات نوعی ما درباب ترجیحات آدمها میان دو کالا را به تصویر میکشد. در الگوهای دیگر، این کالاها غالباً کالاهای مصرفی از قبیل غذا یا لباس خواهند بود و شخص را نیز با عنوان مصرفکننده خواهیم نامید. در الگویی که اینجا از ترجیحات یک دانشجو ارائه کردیم، کالاها «نمره پایانی» و «زمان آزاد» هستند. توجه داشته باشید که:
- منحنیهای بیتفاوتی، بهدلیل هزینهفایدهها یا بدهبستانها، شیب روبهپایین دارند: اگر دو ترکیب برای شما علیالسویه است، ترکیبی که سهم بیشتری از یک کالا دارد قاعدتاً سهم کمتری از کالای دیگر خواهد داشت.
- هرچه منحنی بیتفاوتی بالاتر باشد، یعنی سطح مطلوبیت بالاتر است: هرچه با دورشدن از نقطه آغاز به سمت بالا و طرف راست نمودار حرکت میکنیم، درواقع به سمت ترکیباتی نزدیک میشویم که سهم بیشتری از هر دو کالا را دارند.
- منحنیهای بیتفاوتی عموماً مسطحاند: تغییرات جزئی در میزان کالاها، جهش عمده در مطلوبیت را بدنبال ندارند.
- منحنیهای بیتفاوتی تقاطع ندارند: (چرا؟ به تمرین ۳.۳ نگاه کنید).
- هرچه در طول یک منحنی بیتفاوتی به سمت راست حرکت میکنید، تختتر میشود.
- نرخ نهایی جانشینی (MRS)
- بده-بستانی که فرد مایل است بین دو کالا انجام دهد. در هر نقطه، این عبارت است از شیبِ منحنی بیتفاوتی. همچنین نگاه کنید به نرخ نهایی تبدیل.
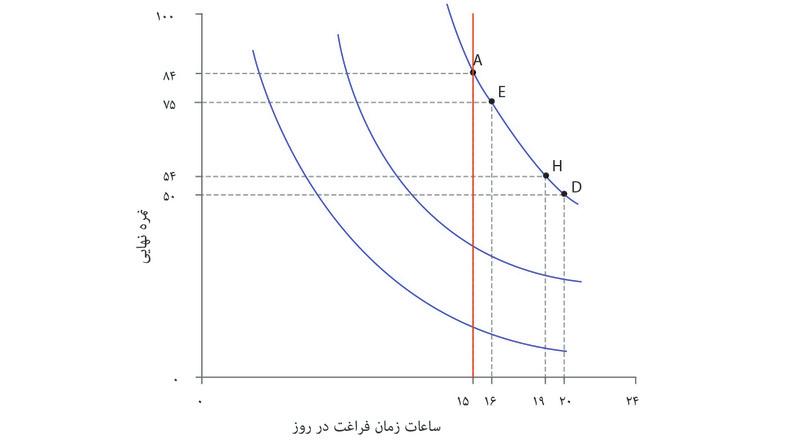
برای فهم آخرین ویژگی فهرستشده، نگاه کنید به منحنیهای بیتفاوتی الکسی که در کنار یکدیگر در شکل ۳.۷ رسم شدهاند. اگر الکسی در نقطه A با ۱۵ ساعت زمان آزاد و نمره ۸۴ باشد، تمایل خواهد داشت که در ازای یک ساعت زمان آزاد بیشتر ۹ نمره خود را از دست بدهد که این او را به نقطه E خواهد برد (فراموش نکنید که A و E برای او علیالسویهاند). در این حالت اصطلاحاً میگوییم که نرخ نهایی جانشینی (MRS) او میان نمره و زمان آزاد در نقطه A برابر ۹ است؛ و همین کاهش نمره است که مطلوبیت الکسی را درنتیجه افزایش یکساعتهی زمان آزاد، ثابت نگه میدارد.
منحنیهای بیتفاوتی، آنطور که ترسیم کردهایم، بهتدریج تختتر میشوند، زیرا قاعدتاً منطقی است که گمان کنیم که هرچه زمان آزاد بیشتر و نمره کمتری داشته باشد، تمایل او در ازدست دادن نمره برای کسب زمان آزاد بیشتر کمتر خواهد بود، و بنابراین نرخ نهایی جانشینی او نیز کمتر خواهد بود. در شکل ۳.۷ نرخ نهایی جانشینی را به ازای هر ترکیب در طول منحنی بیتفاوتی محاسبه کردهایم. میتوانید ببینید که وقتی الکسی زمان آزاد بیشتر و نمره کمتری داشته باشد، نرخ نهایی جانشینی او – یعنی تعداد نمرهای که مایل است برای کسب زمان آزاد بیشتر ازدست بدهد – نیز بهتدریج افت خواهد کرد.
نرخ نهایی جانشینی همان شیب منحنی بیتفاوتی است و هرچه روی منحنی به سمت راست حرکت کنیم، افت میکند. اگر در شکل ۳.۷ بخواهید از یک نقطه به نقطهای دیگر حرکت کنید، خواهید دید که اگر مقدار زمان آزاد را افزایش دهید منحنیهای بیتفاوتی تختتر و اگر نمره را افزایش دهید، پرشیبتر خواهند شد. وقتیکه زمان آزاد نسبت به تعداد نمره کم است، بدین معناست که الکسی تمایل کمتری برای از دست دادن یک ساعت زمان آزاد در ازای نمرهی بالاتر دارد: به عبارتی دیگر نرخ نهایی جانشینی او بالا و منحنی بیتفاوتی او پرشیب است.
همانطور که خطوط جانبی روی نمودار نشان میدهد، اگر روی خط عمودی و تا نقطهی ۱۵ ساعت به سمت بالا حرکت کنید، منحنیهای بیتفاوتی شیبدارتر میشوند: یعنی نرخ نهایی جانشینی افزایش پیدا میکند. در یک میزان معین از زمان آزاد، الکسی حاضرست بهازای یک ساعت زمان اضافی، نمرههای بیشتری را از دست بدهد و این زمانی است که نمرات زیادی داشته باشد و نه نمرات کم(مثلا اگر با خطر افتادن در درس روبهرو باشد). زمانیکه به نقطهی A میرسید یعنی جایی که نمره برابر با ۸۴ است، نرخ نهایی جانشینی بالاست؛ یعنی نمرات در این نقطه آنقدر زیادند که او به ازای یک ساعت زمان فراغت بیشتر حاضرست ۹ نمره را از دست بدهد.
Leibniz: Indifference curves and the marginal rate of substitution
همین تاثیر را در صورتیکه نمره را ثابت نگه دارید و مقدار زمان آزاد را جابهجا کنید وجود خواهد داشت. اگر در طول خط افقی و برای نمره ۵۴ به سمت راست حرکت کنید، نرخ نهایی جانشینی در هر منحنی بیتفاوتی کمتر میشود. هرچه زمان آزاد بیشتر میشود، الکسی تمایل کمتر و کمتری برای از دست دادن نمره در ازای زمان بیشتر پیدا میکند.
تمرین ۳.۳ چرا منحنیهای بیتفاوتی هیچگاه یکدیگر را قطع نمیکنند؟
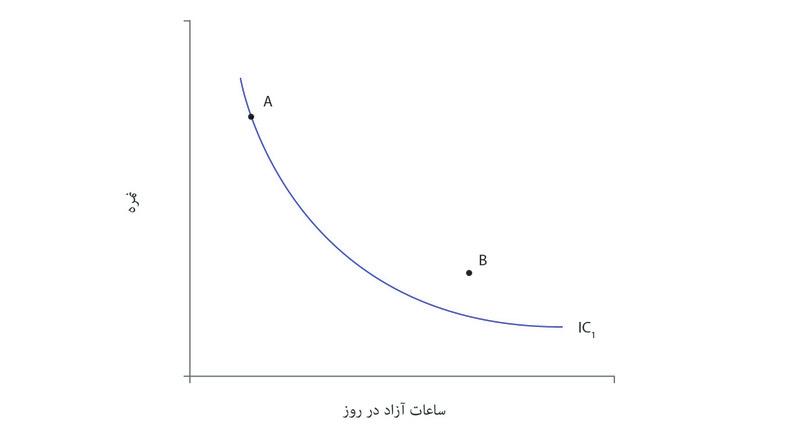
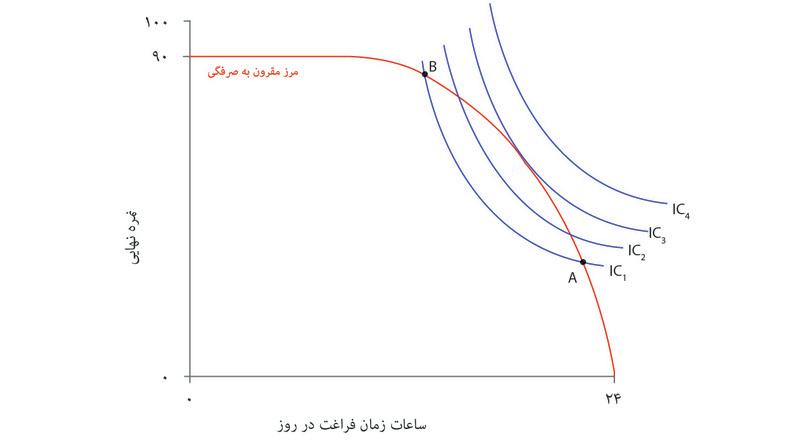
در نمودار زیر , IC۱ منحنی بیتفاوتی است که کلیه ترکیباتی را که سطح مطلوبیتی برابر با A دارند بهم وصل می کند. ترکیب B روی خط IC ۱قرار ندارد.
![]()
- آیا ترکیب B مطلوبیت بیشتر یا کمتری نسبت به ترکیب َ Aدارد؟ از کجا میدانید؟
- طرحی از نمودار رسم کنید و منحنی بیتفاوتی دیگری یعنی IC۲را اضافه کنید که از نقطه B میگذرد و IC۱را قطع میکند. محل تقاطع آنها را با علامت Cمشخص کنید.
- ترکیبهای B و C هر دو روی منحنی IC۲قرار دارند. این چه معنایی از نظر سطح مطلوبیت آنها دارد؟
- ترکیبهای C و A هر دو روی منحنی IC۱قرار دارند. این چه معنایی از نظر سطح مطلوبیت آنها دارد؟
- بر اساس پاسخهایی که به سوالات 3 و 4 میدهید، چگونه سطح مطلوبیت در ترکیبهای A و B را مقایسه میکنید؟
- حالا پاسخ سوالهای ۱ و ۵ را مقایسه کنید و توضیح دهید که از کجا میفهمید منحنیهای بیتفاوتی هرگز یکدیگر را قطع نمیکنند؟
تمرین ۳.۴ نرخ نهایی جانشینی
تصور کنید در پایان تحصیلات دانشگاهی شغلی به شما پیشنهاد شده است که به ۴۰ ساعت کار در هفته نیاز دارد. این کار ۱۲۸ ساعت زمان آزاد در هفته برای شما باقی خواهد گذاشت. درآمد هفتگی که انتظار دریافتش را دارید تخمین بزنید (و واقعگرا باشید!).
- نموداری را ترسیم کنید که زمان آزاد را روی محور افقی و پرداخت هفتگی را روی محور عمودی نشان میدهد و ترکیب متناظر با پیشنهاد شغلیتان را که آنرا A مینامیم را نیز رسم کنید. تصور کنید که حدود ۱۰ ساعت در روز به خواب و خوراک نیاز دارید و بنابراین ممکن است بخواهید محور افقی را با ۷۰ ساعت در نقطهی شروع ترسیم کنید.
- حالا منحنی بیتفاوتی را طوری رسم کنید که A بیانگر تعداد ساعتی که شما خودتان انتخاب کردهاید باشد.
- حالا تصور کنید شغل دیگری به شما پیشنهاد شده است که مستلزم ۴۵ ساعت کار در هفته است. با استفاده از منحنی بیتفاوتیای که رسم کردهاید، سطح پرداخت هفتگیای را که باعث خواهد شد این پیشنهاد با پیشنهاد اولیه برای شما بیتفاوت باشد تخمین بزنید.
- همین کار را در مورد شغل دیگری که مستلزم ۳۵ ساعت کار در هفته است انجام دهید. چه سطحی از پرداخت هفتگی باعث خواهد شد که این گزینه و گزینه اصلی برای شما بیتفاوت باشد؟
- با استفاده از نمودارتان، نرخ نهایی جانشینی خود میان پرداخت و زمان آزاد در نقطه A را محاسبه کنید.
پرسش ۳.۴ (یک پاسخ را انتخاب کنید)
شکل ۳.۶ منحنیهای بیتفاوتی الکسی برای زمان آزاد و نمرهی نهایی را نشان میدهد.کدامیک از گزینههای زیر صحیح است؟
- (الف) منحنی بیتفاوتی روی نقطه C کمتر از منحنی روی نقطه B است. بنابراین الکسی B را به C ترجیح می دهد.
- (ب) نقطه A یعنی جایی که الکسی نمره ۸۴ و ۱۵ ساعت زمان آزاد دارد، و نقطه B یعنی جایی که نمره ۵۰ و ۲۰ ساعت زمان آزاد دارد، هردو روی یک منحنی بیتفاوتی واحد قرار دارند.
- در نقطه D، الکسی همین مقدار زمان آزاد اما نمره بهتری دارد.
- بده-بستان معکوس صحیح است: الکسی با رفتن از نقطه G به D تمایل دارد که ۱۰ نمره را در ازای ۲ ساعت زمان آزاد اضافی از دست بدهد. اما اگر از نقطه G به E برود، درواقع تمایل دارد که ۲ ساعت زمان آزاد را در ازای ۱۵ نمره اضافی از دست بدهد.
پرسش ۳.۵ پاسخ (های) صحیح را انتخاب کنید.
نرخ نهایی جانشینی (MRS) چیست؟
- • نرخِ نهایی جانشینی نمایانگرِ نسبتِ مبادله در نهایت را نشان میدهد، به عبارت دیگر، اینکه چه مقدار از یک کالا را مصرفکننده مایل است در برابر یک واحد اضافی از کالای دیگر از دست بدهد.
- • این همان تعریف نرخ نهایی جانشینی است.
- • نرخ نهایی جانشینی عبارت است از مقداری از یک کالا که میتواند جایگزینِ یک واحد از کالای دیگر شود بدونِ آنکه کارائی تغییر کند.
- • شیب منحنی بیتفاوتی نمایانگر نرخ نهایی جانشینی است: یعنی مبادلهای میان دو کالا که کارائی را ثابت نگه میدارد.
۳.۳ هزینهی فرصت
- هزینه فرصت
- ازآنجاکه انجام هر اقدامی به معنای پشتسرگذاشتنِ بهترین گزینه بعدی است، هزینه فرصت عبارت است از سودِ خالصِ ناشی از جایگزینِ پشتسرگذاشته شده.
الکسی با یک تنگنا روبرو است: با نگاهی به ترجیحات او متوجه خواهیم شد که او میخواهد هم نمره و هم زمان آزاد او در بیشترین حد ممکن باشد. اما با توجه به تابع تولیدش، او نمیتواند زمان آزاد خود را افزایش دهد مگر اینکه نمره پایینتری در امتحان بگیرد. راه دیگر بیان این نکته این است که بگوییم زمان آزاد واجد یک هزینهی فرصت: است برای دستیابی به زمان آزاد بیشتر، الکسی باید فرصت بدست آوردن نمره بالاتر را از دست بدهد.
در علم اقتصاد هزینهی فرصت هنگامی معنا پیدا میکند که موضوع مطالعه افرادی هستند که قرارست میان چند اقدام جایگزین و متقابلا ناهمپوشان انتخاب کنند. در فصل دو اتخاذ اقدام A در مقایسه با اقدام B یا همان «بهترین گزینهی بعدی» را ارزیابی کردیم. وقتی هزینهی اتخاذ اقدام A را در نظر میگیریم درواقع این واقعیت را به حساب میآوریم که اگر اقدام A را انجام بدهیم دیگر نمیتوانیم اقدام B را اتخاذ کنیم. بنابراین «انجام ندادن B »به بخشی از هزینهی انجام دادن A بدل میشود. این را هزینهی فرصت مینامیم چرا که انجام دادن A به معنای صرفنظر کردن از فرصت انجام B است.
تصور کنید که از یک حسابدار و یک اقتصاددان خواسته شده است تا هزینهی رفتن به یک کنسرت، یعنی اقدام A، در یک سالن تئاتر را گزارش کنند که هزینهی بلیط آن ۲۵ دلارست. در پارکی کنار سالن تئاتر کنسرت B برقرارست که رایگان اما بطور همزمان برگزار میشود.
- حسابدار
- هزینهی کنسرت A، هزینهای است که «از جیب» پرداخت میکنید: یعنی ۲۵ دلار برای بلیط میپردازید پس هزینه برابرست با ۲۵ دلار.
- اقتصاددان
- اما برای رفتن به کنسرت A چه چیزی را باید از دست بدهید؟ ۲۵ دلار را از دست میدهید بعلاوه لذت کنسرت رایگان در پارک را. بنابراین هزینهی کنسرت Aبرای شما عبارتست از هزینهای که از جیب میدهید بعلاوه هزینهی فرصت.
تصور کنید که (اگر کنسرت پارک رایگان نبود)حداکثر هزینهای که برای شرکت در کنسرت رایگان در پارک مایل بودید بپردازید ۱۵ دلار باشد. بهترین گزینهی بعدی برای جایگزینی کنسرت A ، یک لذت ۱۵ دلاری در پارک خواهد بود. این هزینهی فرصت رفتن به کنسرت A است.
- هزینه اقتصادی
- هزینهی نقدی یک اقدام، بعلاوه هزینهی فرصتِ آن.
بنابراین کل هزینهی اقتصادی کنسرت A عبارتست از: ۲۵+۱۵= ۴۰ دلار. اگر لذتی که از حضور در کنسرت A انتظار دارید بیش از هزینهی اقتصادی آن باشد مثلا ۵۰ دلار، آنوقت از کنسرت B صرفنظر خواهید کرد و یک بلیط برای سالن تئاتر خواهید خرید. از سوی دیگر، اگر هزینهی لذت کنسرت Aرا ۳۵ دلار تخمین بزنید، آنوقت هزینهی اقتصادی ۴۰ دلاری به این معنا خواهد بود که رفتن به سالن تئاتر را انتخاب نخواهید کرد. به عبارت ساده تر با توجه به اینکه شما باید ۲۵ دلار برای بلیط بپردازید به جای آن کنسرت B را انتخاب خواهید کرد و با این کار ۲۵ دلار برای هزینه در امور دیگر پسانداز خواهید کرد و از ارزش سود ۱۵ دلاری کنسرت رایگان در پارک لذت خواهید برد.
چرا حسابدارها اینطور فکر نمیکنند؟ چون که شغلشان این نیست. حسابدارها حقوق میگیرند تا پول را ردیابی کنند نه اینکه عوایدی برای تصمیمگیری در مورد نحوهی انتخاب میان گزینههایی که برخی از آنها هم قیمت اعلامشده ندارند، فراهم کنند. اما اتخاذ تصمیمات معقول و پیشبینی اینکه انسانهای معقول چگونه تصمیم میگیرند، مستلزم کاری بیش از ردیابی پول است. یک حسابدار ممکن است استدلال کند که کنسرت پارک اساسا نامربوط است:
:حسابدار بودن یا نبودن کنسرت رایگان در پارک تاثیری بر هزینهی رفتن به کنسرت A ندارد. درهر حال هزینه برای شما ۲۵ دلارست.
:اقتصاددان اما بودن یا نبودن کنسرت رایگان در پارک میتواند بر اینکه شما به کنسرت Aبروید تاثیر بگذارد، زیرا گزینههای موجود شما را تغییر میدهد. اگر لذت از کنسرت A هزینهای معادل ۳۵ دلار دارد و بهترین گزینهی بعدی ماندن در خانه و یک لذت صفر دلاری یا رایگان باشد، شما کنسرت Aرا انتخاب خواهید کرد اما اگر کنسرت B موجود باشد شما آنرا به A ترجیح خواهید داد .
- بهره اقتصادی
- هرگونه پرداخت یا سایر مزایایی که فرد بالاتر و علاوه بر آنچه در بهترین گزینه بعدی خود (یا گزینه ذخیره خود) بدست میآورد، بدست آورده باشد. همچنین نگاه کنید به: گزینه ذخیره
در فصل دو گفتیم که اگر یک اقدام سود خالص بیشتری نسبت به بهترین گزینهی بعدی در برداشته باشد، آن اقدام واجد یک بهرهی اقتصادی خواهد بود و شما آنرا انجام خواهید داد. راه دیگر گفتن این مسأله این است که شما هنگامی با اتخاذ یک اقدام بهره اقتصادی دریافت میکنید که آن اقدام سودی بیشتر از هزینهی اقتصادی آن (یعنی مجموع هزینهی از جیب و هزینهی فرصت) داشته باشد.
شکل ۳.۸ مثال مربوط به انتخاب کنسرت را خلاصه میکند
| ارزش بالای تاتر، انتخاب(A) | ارزش پایین تاتر، انتخاب(A) | |
|---|---|---|
| پول از جیبت (قیمت بلیت A) | $۲۵ | $۲۵ |
| هزینه فرصت (لذت فراموش شده B، کنسرت در پارک) | $۱۵ | $۱۵ |
| هزینه اقتصادی (مجموع پول از جیب و هزینه فرصت) | $۴۰ | $۴۰ |
| لذت از تاتر (A) | $۵۰ | $۳۵ |
| بهره اقتصاد (لذت منهای هزینه اقتصادی)) | $۱۰ | −$۵ |
| تصمیم | A: به یک سالن تاتر بروی. | B: به یک تاتر در پارک بروی. |
کدام کنسرت را انتخاب میکنید؟ هزینه فرصت و بهره اقتصادی
شکل ۳.۸ کدام کنسرت را انتخاب میکنید؟ هزینه فرصت و بهره اقتصادی
پرسش ۳.۶ (یک پاسخ را انتخاب کنید)
تصور کنید که یک راننده تاکسی در ملبورن هستید که روزی ۵۰ دلار استرالیا درآمد دارد. به شما یک بلیط یک روزه برای مسابقات اُپن استرالیا به قیمت ۴۰ دلار استرالیا پیشنهاد شده است. چون یک طرفدار جدی تنیس هستید، این تجربه را ۱۰۰ دلار ارزیابی میکنید. بنابراین:
- (الف) با رفتن به مسابقات اُپن، درواقع فرصت بهدستآوردنِ ۵۰ دلار از کار روی تاکسی را ازدست میدهید. این هزینه فرصت شما است.
- (ب) هزینه اقتصادی عبارت است از مجموع قیمتِ واقعیای که میپردازید و بعلاوهی هزینه فرصت که در این مورد عبارت است از: ۴۰ دلار + ۵۰ دلار = ۹۰ دلار.
- (ج) بهره اقتصادی یک اقدام عبارت است از سود آن منهای هزینه اقتصادی آن (هزینه جیب به علاوه هزینه فرصت). بنابراین بهره اقتصادی عبارت است از: ۱۰۰ دلار – ۴۰ دلار – ۵۰ دلار = ۱۰ دلار.
- (د) حداکثر قیمتی که باید برای بلیط پرداخته باشید عبارت است از قیمتی که در آن بهره اقتصادی شما برابر صفر باشد که در این مورد برابر با ۵۰ دلار است.
تمرین ۳.۵ هزینهی فرصت
دولت بریتانیا در سال ۲۰۱۲ قانونی را تصویب کرد که به دانشگاهها اختیار میداد شهریههایشان را افزایش دهند. اغلب دانشگاهها تصمیم گرفتند که شهریهی سالانهشان را از ۳۰۰۰ دلار به ۹۰۰۰ دلار افزایش دهند.
آیا این به آن معناست که هزینه رفتن به دانشگاه سه برابر شده است؟ (فکر کنید که یک حسابدار و یک اقتصاددان احتمالاً چگونه به این سوال پاسخ خواهند داد.)
۳.۴ مجموعهی مقرونبهصرفه
اجازه بدهید دوباره به مسأله نحوه انتخاب الکسی میان نمره و زمان آزاد برگردیم. زمان آزاد هزینه فرصتی دارد که درقالب تعداد ازدسترفتهی نمرات خود را نشان میدهد (یا معادل با آن، میتوان گفت که درصد نمره هزینه فرصتی دارد که درقالب تعداد ساعات ازدسترفته از زمان آزاد برای کسب آن نمره خود را نشان میدهد). اما پیش از آنکه نشان دهیم چگونه الکسی این معما را حل خواهد کرد، لازم است که گزینههای جایگزینی که پیشروی او هستند را دقیقاً استخراج کنیم.
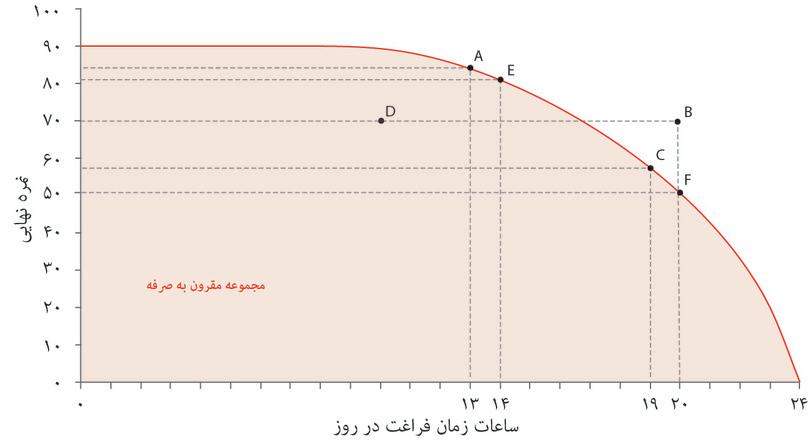
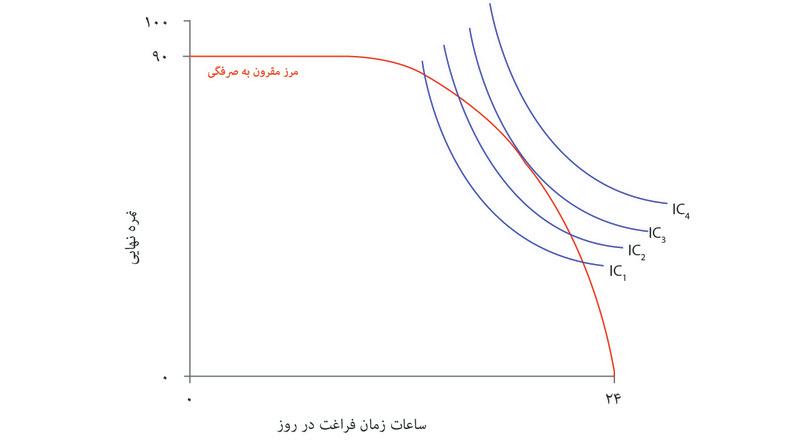
برای پاسخ به این سوال، دوباره به تابع تولید نگاه میکنیم. این بار نشان میدهیم که چگونه نمره پایانی به زمان آزاد بستگی دارد و نه زمان مطالعه. هر روز ۲۴ ساعت است. الکسی باید این زمان را میان مطالعه (کلیه ساعاتی که به یادگیری اختصاص پیدا میکنند) و زمان آزاد (و کل زمان باقیماندهاش) تقسیم کند. شکل ۳.۹ رابطه میان نمره پایانی و تعداد ساعت زمان آزاد در هر روز را نشان میدهد – که تصویر معکوس شکل ۳.۵ است. اگر الکسی کل ۲۴ ساعت را به مطالعه بگذراند این بدان معناست که هیچ زمان آزادی نخواهد داشت و نمره ۹۰ خواهد گرفت. و در فرض میگیریم که اگر ۲۴ ساعت زمان آزاد در روز را انتخاب کند، نمره صفر خواهد گرفت.
- مرز مقرونبهصرفهبودن
- منحنی که از نقاطی تشکیل شده است که اکثریت مقدار احتمالی یک کالا برای مقدار داده شده از یک کالای دیگر است.
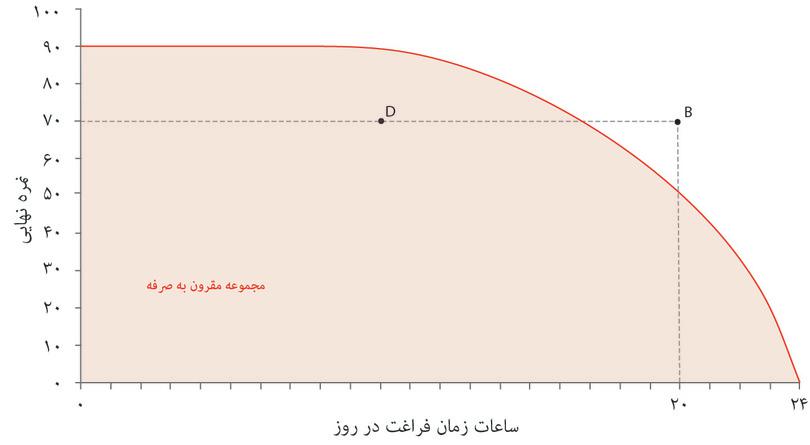
در شکل ۳.۹ محورها را نمره پایانی و زمان آزاد تشکیل میدهند، دو کالایی که برای الکسی مطلوبیت بههمراه دارند. اگر فکر کنیم که او ترکیبی از این دو کالا را برای مصرف انتخاب خواهد کرد، آنگاه خط منحنی در شکل ۳.۹ نشان میدهد که چه چیز مقرون بهصرفه است. درواقع مرز مقرونبهصرفهبودنرا برای او نشان میدهد: یعنی بالاترین نمرهای که باتوجه به میزان زمان آزادی که کنار میگذارد، خواهد گرفت. بااستفاده از خطوط جانبی ببینید که چه ترکیباتی از نمره و زمان آزاد مقرون بهصرفه هستند، و کدام ترکیبها مقرون بهصرفه نیستند، و چگونه انحنای خط مرزی، هزینهی فرصت زمان آزاد را نشان میدهد.
- مرز مقرونبهصرفهبودن
- منحنی که از نقاطی تشکیل شده است که اکثریت مقدار احتمالی یک کالا برای مقدار داده شده از یک کالای دیگر است.
هر ترکیبی از زمان آزاد و نمره که داخل یا روی مرز قرار بگیرد مقرون بهصرفه است. ترکیباتی که بیرون از مرز مقرون بهصرفهگی قرار بگیرند، با توجه به قابلیتها و شرایط مطالعه الکسی، غیر مقرون بهصرفه محسوب میشوند. از سوی دیگر، اگرچه هر ترکیب داخل مرز مقرون بهصرفه محسوب میشود، اما انتخاب آن به این معناست که الکسی چیزی را که درعمل برایش ارزش قائل است، کنار میگذارد. اگر روزی ۱۴ ساعت مطالعه میکرد، آنوقت براساس الگوی ما، میتوانست نمره ۸۹ را برای خود تضمین کند. اما اگر قبل از پایان امتحان دست از نوشتن میکشید، ممکن بود نمره کمتری (مثلاً ۷۰) بگیرد. احتمالاً دورریختن نمره به این شکل و بیهیچ دلیلی احمقانه است، اما ناممکن نیست. راه دیگر برای بهدست آوردن یک ترکیب داخل مرز این است که در کتابخانه بنشیند و هیچکاری نکند – که به این معناست که الکسی از زمان آزادی کمتر از میزانی که در دسترس اوست استفاده کند، که بازهم بیمعناست.
با انتخاب یک ترکیب داخل مرز، الکسی چیزی را ازدست میدهد که بطور رایگان دراختیار اوست – یعنی چیزی که هیچ هزینه فرصتی در پی ندارد. او میتوانست بدون از دست دادن هیچ زمان آزادی نمره بیشتر بگیرد، یا بدون کاستن از نمرهاش زمان آزاد بیشتری داشته باشد.
مرز مقرون بهصرفهگی، حد یا محدودیتی بر انتخابهای الکسی است. نمایانگر بدهبستان یا هزینهفایدهای است که باید میان نمره و زمان آزاد انجام دهد. در هر نقطهای روی مرز، در اختیارگرفتن زمان آزاد بیشتر هزینه فرصتی دارد که درقالب نمرات ازدست رفته خود را نشان میدهد و متناظر با شیب خط مرزی است.
- نرخ نهایی تبدیل(MRT)
- تعداد کالایی که باید برای دستیابی به یک واحد اضافی از کالایی دیگر قربانی شود. در هر نقطه، این عبارت است از شیبِ مرزِ مقرونبهصرفگی. همچنین نگاه کنید به نرخ نهایی جانشینی.
این ایده را بهشکل دیگری هم میتوان بیان کرد؛ اینکه بگوییم مرز مقرون بهصرفهگی نمایانگر نرخ نهایی تبدیلاست: نرخی که الکسی میتواند زمان آزاد را به نمره تبدیل کند. دوباره در شکل ۳.۹ به شیب خط مرزی میان نقاط A و E نگاه کنید:
- شیب خط AE (فاصله عمودی تقسیم بر فاصله افقی) برابر با ۳- است.
- در نقطه A، الکسی میتواند یک واحد زمان آزاد بیشتری را در ازای از دست دادن ۳ نمره بدست بیاورد. هزینه فرصت یک واحد از زمان آزاد ۳ نمره است.
- در نقطه E الکسی میتواند یک واحد زمان آزاد را با ۳ نمره تعویض کند. نرخ نهایی برای تبدیل زمان آزاد به نمره ۳ است.
توجه داشته باشید که شیب خط AE تنها تخمینی از شیب مرز است. به عبارت دقیقتر، شیب در هر نقطه، شیب خط مماس است و این نمایانگر هم نرخ نهایی تبدیل و هم هزینه فرصت در آن نقطه است.
توجه داشته باشید که ما اکنون دو بدهبستان یا هزینهفایده را شناسایی کردهایم:
لایبنیتز: نرخ نهایی تبدیل و نرخ نهایی جانشینی
- نرخ نهایی جانشینی (MRS ): همانطور که در بخش قبل دیدیم، نرخ نهایی جایگزینی سنجهای است برای اندازهگیری بدهبستانی که الکسی مایل است میان نمره امتحان و زمان آزاد انجام دهد.
- نرخ نهایی تبدیل (MRT): اما درعوض نرخ نهایی تبدیل، بدهبستانی را میسنجد که الکسی بواسطه مرز مقرون بهصرفهگی محدود و مقید به انجام آن است.
همانطور که در بخش بعدی خواهیم دید، انتخابی که الکسی میان نمره و زمان آزادش میکند، به تعادلی میان این دو بدهبستان خواهد رسید.
پرسش ۳.۷ (همه پاسخهای صحیح را انتخاب کنید)
به شکل ۳.۵نگاه کنید که تابع تولید الکسی را نشان میدهد: اینکه چطور نمره پایانی (یا خروجی) به تعداد ساعات صرفشده برای مطالعه (ورودی) بستگی دارد.
زمان آزاد در هر روز عبارت است از ۲۴ ساعت منهای زمان اختصاص یافته به مطالعه در هر روز. مجموعه مقرون به صرفه ترکیبات نمره و ساعات مطالعه روزانهی الکسی توجه کنید. به این ترتیب:
- (الف) پیشاپیش میدانیم که ساعت زمان آزاد در روز عبارت است از ۲۴ ساعت منهای ساعات مطالعه در روز. بنابراین، تعداد ساعتی که صرف خوابیدن شده پیشاپیش در زمان آزاد محاسبه شده است.
- (ب) باتوجه به این واقعیت که تابع تولید دقیقاً معادل مرز مقرون به صرفهگی است مگر اینکه معکوسِ زمان آزاد (یعنی ساعات مطالعه) را به عنوان ورودی آن درنظر بگیریم، بنابراین اولی همان دومی است که در راستای محور X و به سطح افقی جابجا شده باشد.
- (ج) تابع تولید پس از ۱۵ ساعت مطالعه روزانه افقی است. بنابراین مرز مقرون به صرفهگی تنها تا نقطه ۹ ساعت زمان آزاد در روز افقی است.
- (د) با توجه به ۲۴ ساعت شبانهروز، ۱۰ ساعت زمان مطالعه معادل ۱۴ ساعت زمان آزاد است، و تولید نهایی نیروی کار (یعنی خروجی اضافی به ازای هر ساعت مطالعه) همان نرخ نهایی تبدیل (یا بدهبستان میان خروجی و نیروی کار اضافی) است، بطوری که این ارزش برابرند.
۳.۵ تصمیم-سازی و کمیابی
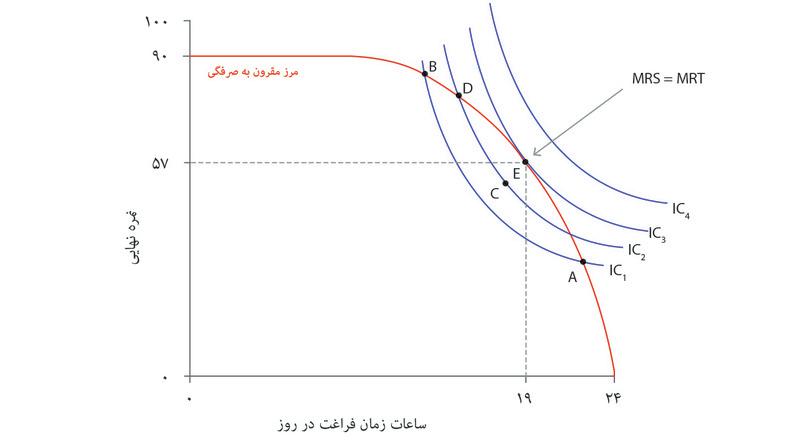
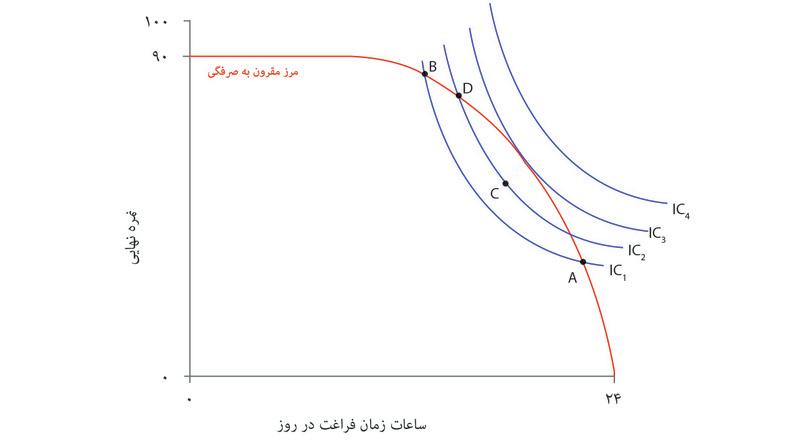
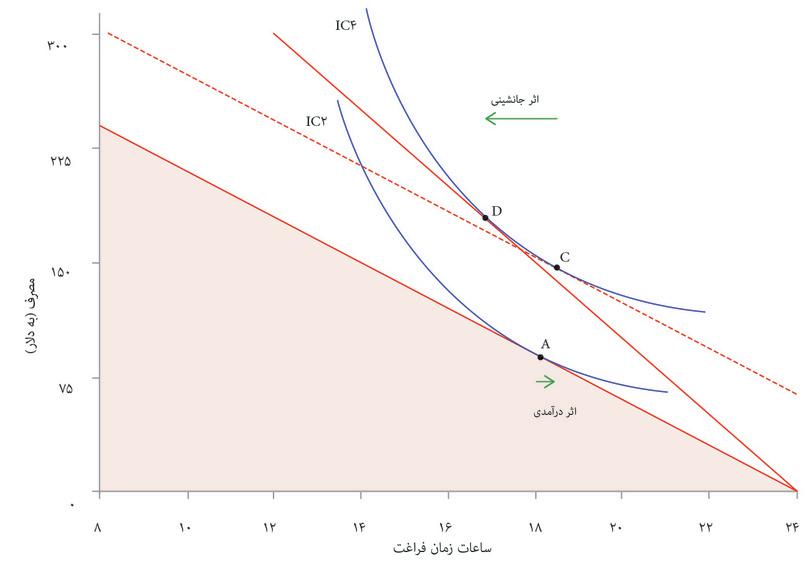
آخرین گام در فرآیند تصمیم-سازی تعیین ترکیبی از نمره نهایی و زمان آزاد است که الکسی انتخاب خواهد کرد. شکل ۳.۱۰ الف مرز مقرون بهصرفهگی (شکل ۳.۹) و منحنیهای بیتفاوتی او (شکل ۳.۶) را کنار هم گذاشته است. بیاد داشته باشید که منحنیهای بیتفاوتی نشاندهنده ترجیحات الکسی، و انحنای آنها نشانگر بدهبستانهایی است که او احتمالاً مایل به انجام آنهاست؛ و مرز مقرون بهصرفهگی حد یا محدودیتی بر انتخابهای او و شیب آن نشانگر بدهبستانی است که او مقید و محدود به انجام آن است.
شکل ۳.۱۰ الف چهار منحنی بیتفاوتی را نشان میدهد که از IC1 تا IC4 نامگذاری شدهاند. منحنی IC4 نمودار بالاترین سطح مطلوبیت است زیرا در دورترین نقطه از نقطه آغاز قرار دارد. بااینحال، هیچ ترکیبی از نمره و زمان آزاد روی منحنی IC4 مقرون بهصرفه نیست زیرا کل منحنی بیتفاوتی بیرون از مجموعه مقرون بهصرفه قرار میگیرد. حالا تصور کنید که الکسی میخواهد ترکیبی داخل مجموعه مقرون بهصرفهگی روی منحنی IC1 را انتخاب کند. اگر طبق مراحل نشانداده شده در شکل ۳.۱۰ الف پیش برویم، خواهیم دید که الکسی میتواند به سمت نقاطی روی منحنیهای بیتفاوتی بالاتر حرکت کند و این کار را تا رسیدن به گزینه مقرون بهصرفهای که حداکثر کارایی را برای او دارد ادامه دهد.
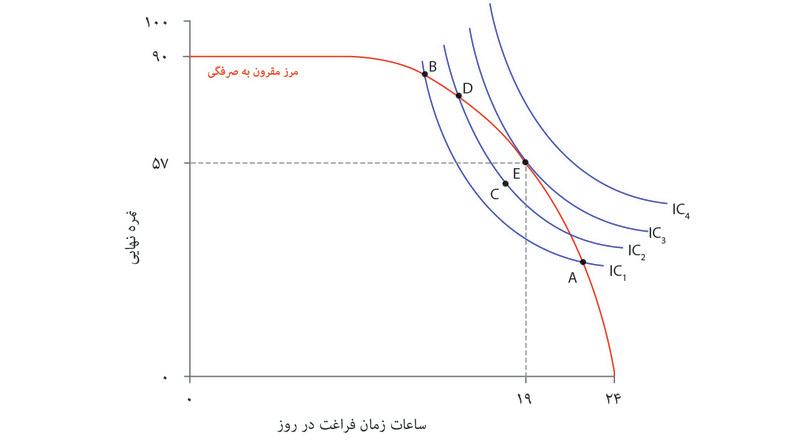
الکسی در نقطه E کاراییاش را به حداکثر میرساند، یعنی نقطه ای که در آن منحنی بیتفاوتی خط مماس بر مرز مقرون بهصرفهگی است. الگو پیشبینی میکند که الکسی،
- ۵ ساعت در روز را به مطالعه و ۱۹ ساعت را به سایر فعالیتها اختصاص خواهد داد
- و بهعنوان نتیجه نمره ۵۷ خواهد گرفت.
همانطور که از روی شکل ۳.۱۰ الف پیداست، در نقطه E مرز مقرون بهصرفهگی و بالاترین منحنی مقرون بهصرفهگی قابل حصول یعنی IC3 هر دو مماس یگدیگرند (تماس پیدا میکنند اما قطع نمیکنند). در نقطه E شیب منحنی بیتفاوتی به اندازه شیب خط مقرون بهصرفهگی است. حالا فراموش نکنید که این شیبها نمایانگر دو بدهبستانی هستند که پیشروی الکسی قرار دارد:
- شیب منحنی بیتفاوتی همان نرخ نهایی جانشینی است: که بدهبستانی است که او مایل است میان زمان آزاد و نمره انجام دهد.
- شیب خط مرزی همان نرخ نهایی تبدیل است: یعنی بدهبستانی که او محدود و مقید است میان زمان آزاد و نمره برقرار کند زیرا فراتر رفتن از مرز مقرون بهصرفهگی ممکن نیست.
اما نقطه ای که در آن الکسی بیشترین کارایی را پیدا میکند جایی است که این دو بدهبستان موازنه پیدا کنند (یعنی نقطه E). ترکیب بهینه نمره و زمان آزاد در نقطه ای است که نرخ نهایی تبدیل با نرخ نهایی جانشینی برابر است.
لایبنیتز: اختصاص بهینه زمان آزاد: نرخ نهایی تبدیل و نرخ نهایی جانشینی برابر میشوند
شکل ۳.۱۰ ب نرخ نهایی جانشینی (یا شیب منحنی بیتفاوتی) و نرخ نهایی تبدیل (یا مرز مقرون به صرفهگی) را در نقاط نشان داده شده در شکل ۳.۱۰ الف نشان میدهد. در نقطه B و D تعداد نقاطی که الکسی مایل است با یک ساعت زمان آزاد معاوضه کند (نرخ نهایی جانشینی) بزرگ تر از هزینه فرصت آن ساعت (یا نرخ نهایی تبدیل) است، بنابراین او ترجیح میدهد که زمان آزادش را بیشتر کند. در نقطه A نرخ نهایی تبدیل بزرگ تر از نرخ نهایی جانشینی است بنابراین او ترجیح میدهد که زمان آزادش را کاهش دهد. و همانطور که انتظار میرود در نقطه E نرخ نهایی جانشینی و نرخ نهایی تبدیل برابر هستند.
| B | D | E | A | |
|---|---|---|---|---|
| اوقات فراغت | ۱۳ | ۱۵ | ۱۹ | ۲۲ |
| نمره | ۸۴ | ۷۸ | ۵۷ | ۳۳ |
| MRT | ۲ | ۴ | ۷ | ۹ |
| MRS | ۲۰ | ۱۵ | ۷ | ۳ |
الکسی چند ساعت را برای مطالعه انتخاب میکند؟
شکل ۳.۱۰ب الکسی چند ساعت را برای مطالعه انتخاب میکند؟
- مسأله انتخاب محدود
- این مسأله درباره این است که چگونه میتوانیم، با توجه به ترجیحات و محدودیتهایمان و وقتی که کالایی که برای آن ارزش قائل هستیم کمیاب است، بهترین اقدام را برای خود انجام دهیم. همچنین نکاه کنید به: مشکل بهینهسازی محدود
ما انتخاب تعداد ساعات مطالعه دانشجو را بر مبنایی الگوسازی کردهایم که آن را مسأله انتخاب محدود مینامیم: به این معنا که یک تصمیم-گیر (الکسی) بدنبال هدفی است (در این مورد حداکثرسازی کارایی) که آن هدف درمعرض محدودیتهایی است (مرز مقرون بهصرفهگی).
در مثال ما همان زمان آزاد و هم نمره امتحان برای الکسی کمیاب محسوب میشوند زیرا:
-
زمان آزاد و نمره هر دو کالا محسوب میشوند: یعنی الکسی برای هر دوی آنها ارزش قائل است.
-
هرکدام یک هزینه فرصت دارند: میزان بیشتر از یکی از آنها به معنای میزان کمتر از آن دیگری است.
در مسائل ناشی از انتخاب محدود، راه حل گزینه بهینه فرد است. اگر هدف الکسی حداکثرسازی کارایی باشد، ترکیب بهینه نمره و زمان آزاد، نقطهای روی مرز مقرون بهصرفهگی است که در آن:
شکل ۳.۱۱ بدهبستانهای الکسی را خلاصه میکند:
| بدهبستان | در کجای نمودار قرار دارد | برابر است با … | |
|---|---|---|---|
| MRS | نرخ نهایی جانشینی: درصد نمراتی که الکسی حاضر است برای اوقات فراغت بدهبستان کند | شیب نمودار بیتفاوتی | |
| MRT، یا هزینه فرصت اوقات فراغت | نرخ نهایی تبدیل: درصدی که الکسی با دادن یا گرفتن یک ساعت آزاد بیشتر به دست میآورد یا از دست میدهد | شیب مرز مقرونبهصرفهبودن | قیمت نهایی تولید کار |
بدهبستانهای الکسی
شکل ۳.۱۱ بدهبستانهای الکسی
تمرین ۳.۶ جستجوی کمبود
وضعیتی را توصیف کنید که در آن نمرات و زمان آزاد الکسی کمیاب نباشد. بیاد داشته باشید که کمیابی هم به ترجیحات یا اولویتهای الکسی و هم به تابع تولید او وابسته است.
پرسش ۳.۸ (یک پاسخ را انتخاب کنید)
شکل ۳.۱۰الف مرز مقرون به صرفگی و منحنی ترجیحات الکسی به ازای نمره نهایی و زمان آزاد او در هر روز را نشان میدهد. تصور کنید که کلیه دانشجویان مرز مقرون به صرفگی یکسانی دارند، اما منحنیهای بیتفاوتی آنها برحسبِ ترجیحاتشان شکل و شیبِ متفاوتی دارند.
با استفاده از دیاگرام مشخص کنید که کدامیک از گزینه های زیر صحیح است:
- (الف) اگر الکسی روی نقطه ای از مرز مقرون به صرفگی قرار داشت که در آن نرخ نهایی جانشینی و نرخ نهایی تبدیل برابراند، آنگاه او احتمالاً مایل خواهد بود مقدار بیشتری از یک کالا که درواقع برای بدست آوردن مقداری از کالای دیگر ضروری است ازدست بدهد. بنابراین، او اینکار را ادامه خواهد داد تا به نقطه ای برسد که در آن نرخ نهایی جانشینی و نرخ نهایی تبدیل برابر باشند.
- (ب) به موازات مرز مقرون به صرفگی، الکسی در نقطه E روی منحنی بیتفاوتی بالاتری خواهد بود تا در نقطه D. بنابراین نقطه D گزینه بهینه نخواهد بود.
- (ج) دانشجویانِ برخوردار از یک منحنی بیتفاوتی تختتر (به این معنا که مایلاند ساعات بیشتری از زمان آزاد را برای کسب مقدار ثابتی از نمره اضافی فدا کنند)، نرخ نهایی جانشینی پائینتری دارند. بنابراین بستههای سمتِ چپِ E (مثلِ D) را انتخاب خواهند کرد، یعنی جایی که منحنیهای بیتفاوتی بر مرز مقرون به صرفگی مماس هستند.
- (د) نقطههایی روی مرز مقرون به صرفگی که در سمت چپ E قرار دارندنرخ بیشتری از نمره نهایی به ازای ساعت زمان آزاد در روز خواهند داشت، اما بهینه نخواهند بود. نقطه بهینه جایی است که در آن نرخ نهایی جانشینی و نرخ نهایی تبدیل برابر باشند.
۳.۶ ساعات کار و رشد اقتصادی
در سال۱۹۳۰ جان مینارد کینز، اقتصاددان بریتانیایی، مقالهای با عنوان احتمالاتِ اقتصادی برای نوادگان ما، منتشر کرد که در آن پیشبینی میکرد که در صد سال آینده، پیشرفت فناوری بطور میانگین ما را ۸ برابر مرفهتر خواهد کرد.2 چیزی که او «مسأله اقتصادی یا همان تنازع برای معاش» مینامید، حلوفصل خواهد شد و دیگر نیازی نخواهد بود که بیشتر از مثلاً ۱۵ ساعت در روز برای برآوردن نیازهایمان کار کنیم. پرسشی که پیش میکشید چنین چیزی بود: با این همه وقت فراغت اضافی چه خواهیم کرد؟
پیشبینی کینز از نرخ پیشرفت اقتصادی در کشورهایی چون بریتانیا و ایالات متحده تقریباً درست بوده، و ساعات کار درواقع کاهش پیدا کرده است اگرچه به میزانی بسیار کمتر از آنچه پیشبینی کرده بود – احتمالاً حتی تا سال ۲۰۳۰ هم میانگین ساعات کاری در هفته به ۱۵ ساعت نخواهد رسید. یک مقاله از تیم هارفورد در بخش مقالات مخفیانه مجله فینانشیل تایمز نشان میدهد که چرا پیشبینی کینز نادرست بود.3
همانطور که در فصل ۲ دیدیم، فناوریهای جدید بهرهوری نیروی کار را بالا میبرند. اکنون ابزارهای لازم برای تحلیل تأثیرات افزایش بهرهوری بر استاندارهای زندگی و خصوصاً درآمد و زمان آزاد کارگران را در اختیار داریم.
تااینجای کار به انتخاب زمان کار و زمان آزاد الکسی را بررسی کردهایم. اکنون الگوی انتخاب محدود خود را به شخص دیگری اعمال خواهیم کرد: آنجلا، کشاورز خودکفایی که تعداد ساعت کاریش را انتخاب میکند. تصور میکنیم که آنجلا غلات را تنها برای صرف شخصی تولید میکند بیآنکه به کس دیگری بفروشد. بهعبارت دیگر اگر غله بسیار کمی تولید کند، گرسنگی خواهد کشید.
چه چیز او را از تولید بیشترین غله ممکن باز میدارد؟ مثل آن دانشجو، برای آنجلا نیز وقت آزاد ارزش دارد – یعنی هم زمان آزاد و هم از مصرف غله برای او کارایی دارد.
اما انتخاب او محدود است: تولید غله به زمان کاری نیاز دارد، و هر ساعت کار به این معناست که آنجلا یک ساعت زمان آزاد از دست میدهد. ساعات زمان آزاد از دست رفته، هزینه فرصت غله تولیدشده است. آنجلا هم مثل الکسی با مسأله کمیابی روبهرو است: او باید میان مصرف غله و مصرف زمان آزاد انتخاب کند.
برای فهم انتخاب او، و تاثیر تحول فناوری بر این انتخاب، نیاز داریم تا تابع تولید او و ترجیحات او را الگوسازی کنیم.
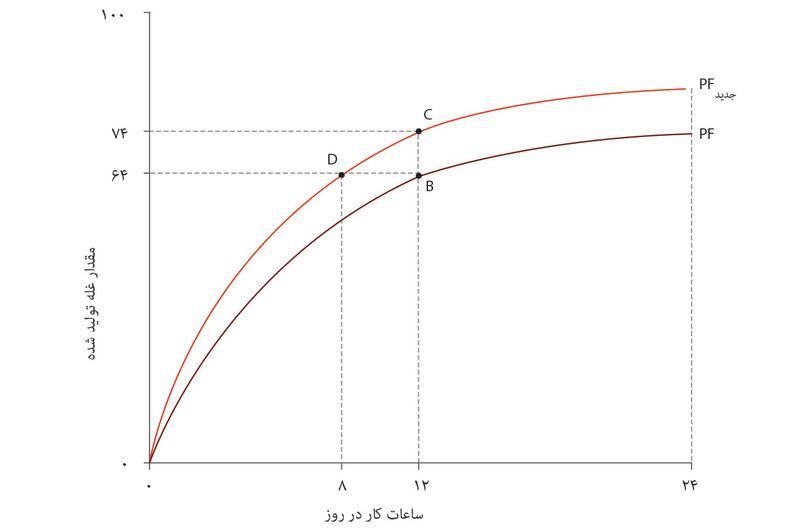
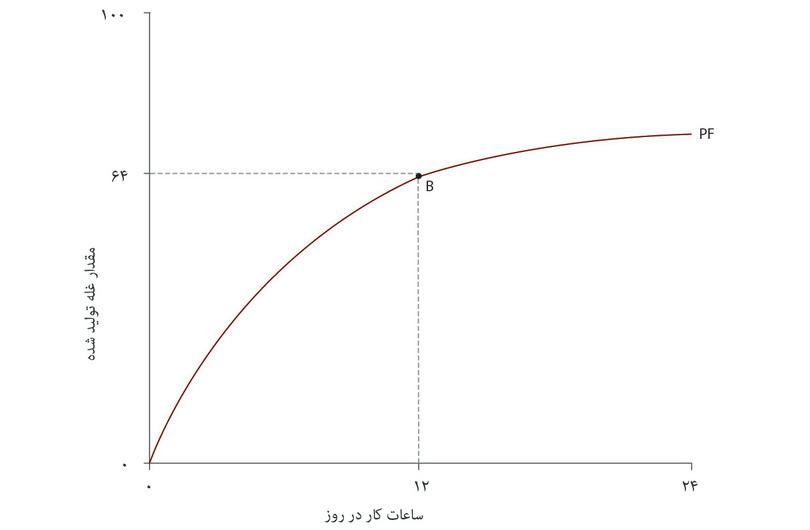
شکل ۳.۱۲ تابع تولید اولیه قبل از وقوع تحول فناورانه را نشان میدهد: یعنی رابطه میان تعداد ساعات کارشده و مقدار غله تولیدشده. توجه داشته باشید که این نمودار هندسی شکل مقعری شبیه به تابع تولید الکسی دارد: محصول نهایی یک ساعت کار اضافی، که توسط شیب نشان داده میشود، با افزایش تعداد ساعات کاهش پیدا میکند.
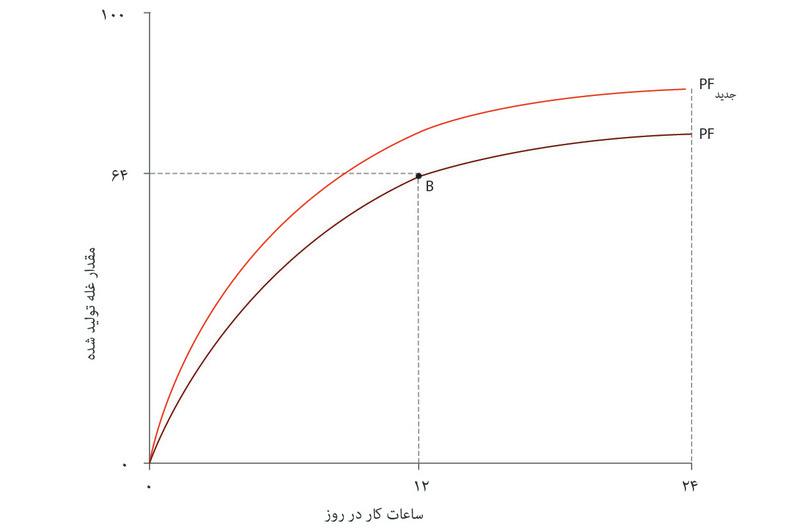
یک پیشرفت فناورانه از قبیل بذر پرمحصولتر یا تجهیزات مناسبتر برای برداشت غله، میزان غله تولیدی در تعداد مشخصی از ساعت را افزایش خواهد داد. تحلیل در شکل ۳.۱۲ تاثیر عملکرد تولید را نشان میدهد.
توجه داشته باشید که تابع تولید جدید، به ازای هر تعداد ساعت مشخص، گودی بیشتری از تابع تولید اولیه دارد. فناوری جدید تولید نهایی نیروی کار آنجلا را بالا برده است: در هر نقطه یک ساعت کار اضافی، غله بیشتری نسبت به میزان متناظر تحت فناوری سابق دارد.
لایبنیتز: الگوسازی تحول فناورانه
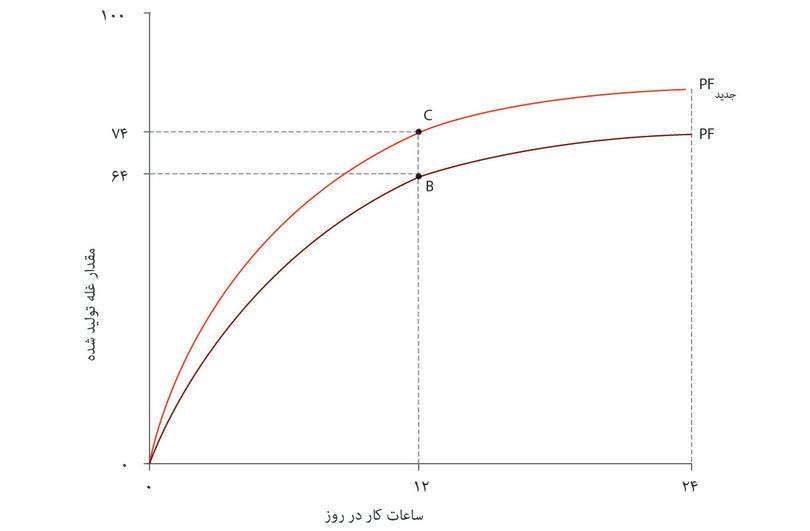
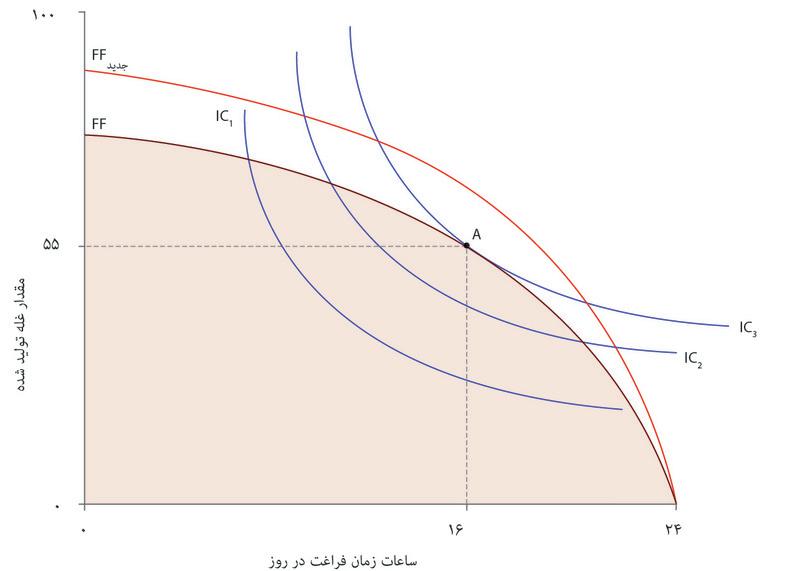
شکل ۳.۱۳ مرز مقرون بهصرفهگی آنجلا را نشان میدهد، که دقیقاً تصویر آینهای تابع تولید، برای فناوری اولیه (FF) و فناوری جدید (FFجدید)است.
مثل سابق، زمان آزاد را به کلیه زمانهایی که برای کار کردن درجهت تولید غله صرف نشده اطلاق میکنیم – که شامل زمان خوردن، خوابیدن، و هر چیز دیگری غیر از کار زراعت، و همچنین زمان فراغت میشود. مرز مقرون بهصرفهگی نشان میدهد که به ازای هر میزان ممکن از زمان آزاد چه مقدار غله میتواند تولید شود. نقاط B،C و D همان ترکیبات زمان آزاد و میزان غله تولیدی مثل جدول ۳.۱۲ را نشان میدهند. شیب خط مرزی نرخ نهایی تبدیل (یعنی نرخ نهایی برای تبدیل زمان آزاد به غله) یا معادل آن، هزینه فرصت زمان آزاد را نشان میدهد. میبینید که پیشرفت فناوری مجموعه مقرون بهصرفه را گسترش میدهد: یعنی گستره بزرگتری از ترکیبات زمان آزاد و غله را دراختیار او قرار میدهد.
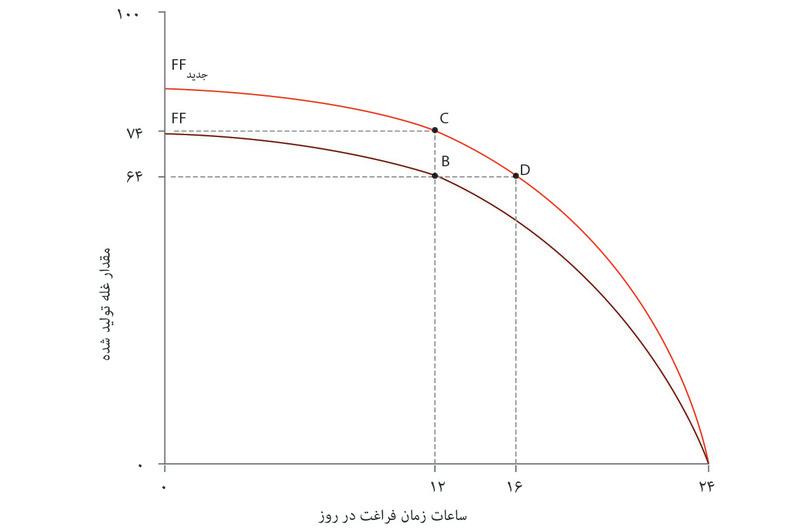
پیشرفت فناوری مجموعه مقرون بهصرفهگی آنجلا را وسیعتر میکند.
شکل ۳.۱۳ پیشرفت فناوری مجموعه مقرون بهصرفهگی آنجلا را وسیعتر میکند.
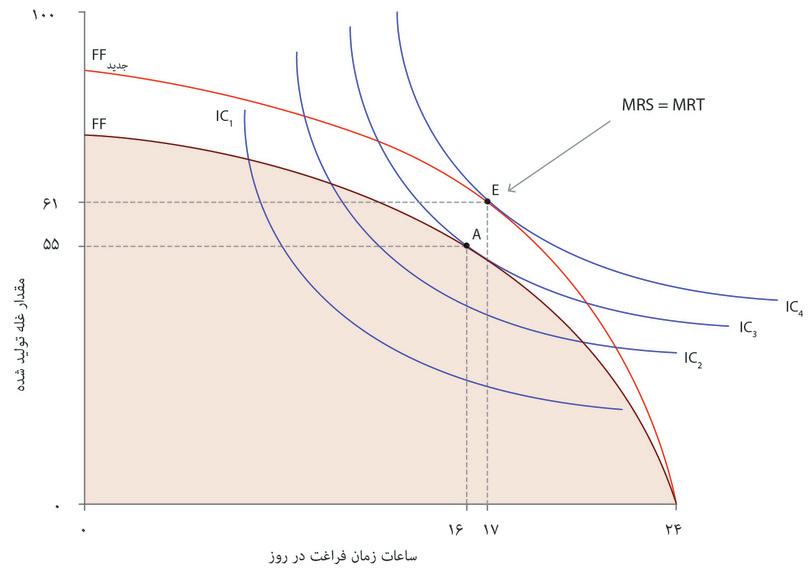
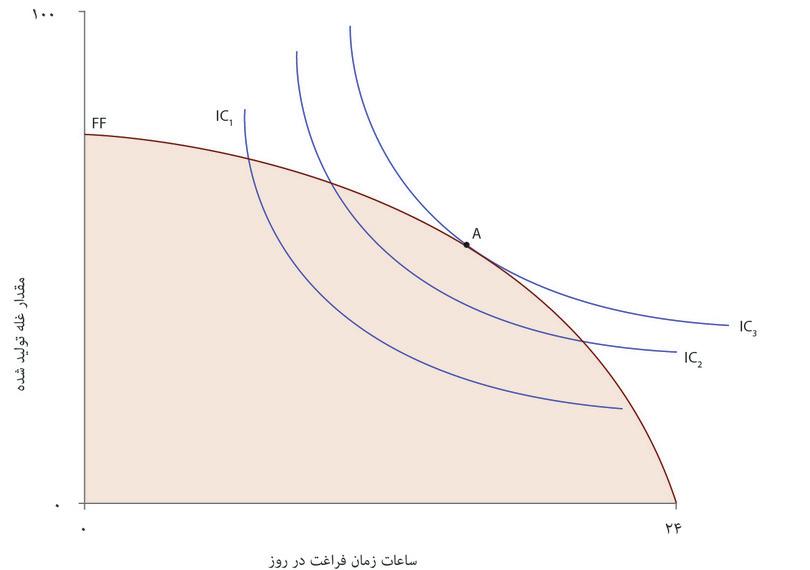
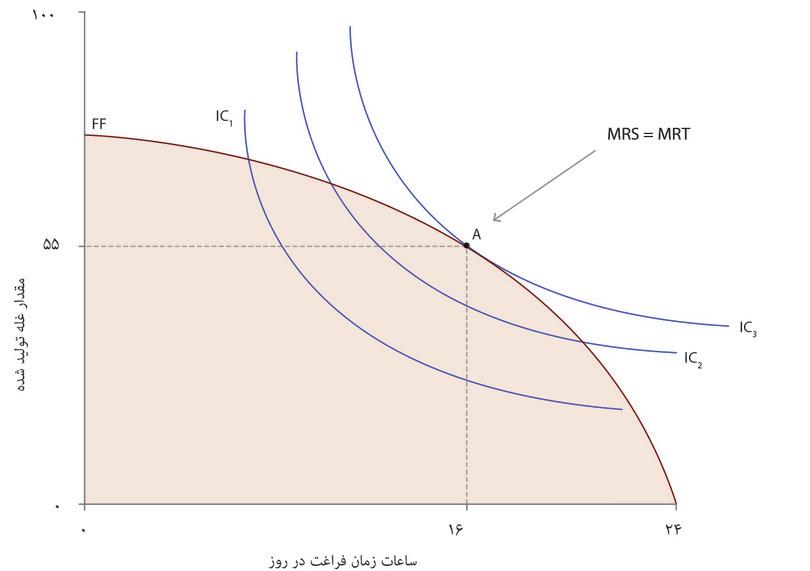
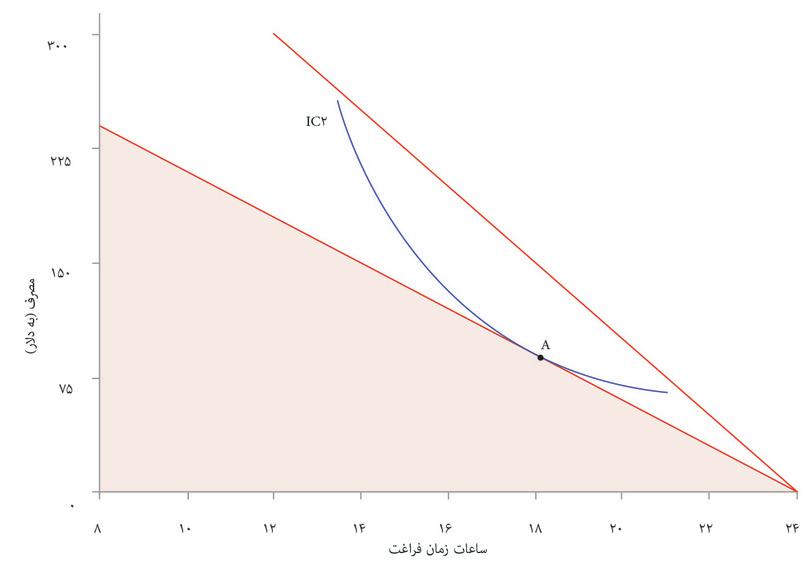
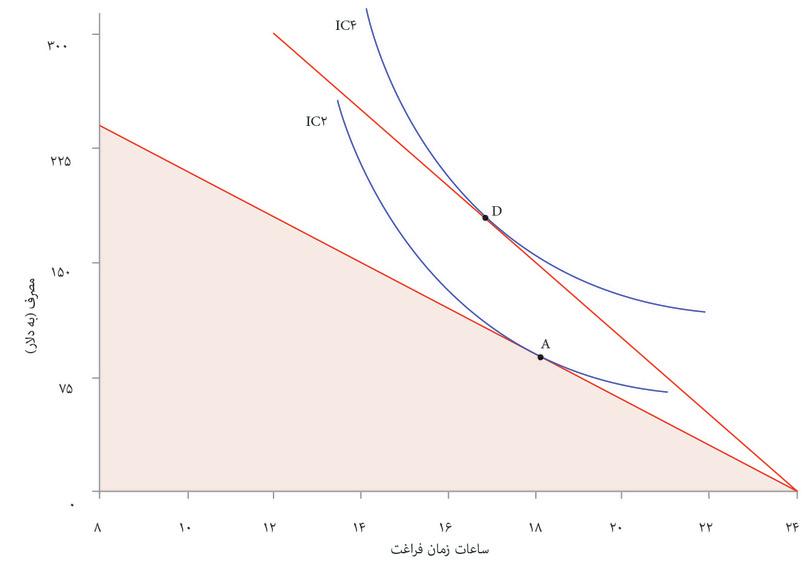
حالا منحنیهای بیتفاوتی آنجلا، که ترجیحات او درخصوص زمان آزاد و مصرف غله را نشان میدهند، را به نمودار اضافه میکنیم تا پیدا کنیم کدام ترکیب در مجموعه مقرون به صرفهگی برای او بهترین است. شکل ۳.۱۴ نشان میدهد که گزینه بهینه تحت فناوری اولیه برای او این است که ۸ ساعت در روز کار کند که درمقابل ۱۶ ساعت زمان آزاد در روز و ۵۵ واحد غله به او خواهد داد. این همان نقطه مماسشدن است، نقطهای که دو معاوضه یا بدهبستان او به توازن میرسند: نرخ نهایی جانشینی میان زمان آزاد و غله (یا شیب منحنی بیتفاوتی) با نرخ نهایی تبدیل (شیب مرز مقرون بهصرفهگی) برابر میشوند. میتوانیم ترکیب زمان آزاد و غله در نقطه A را به عنوان سنجهای برای سنجش استاندارد زندگی او درنظر بگیریم.
با استفاده از خطوط فرعی، ببینید که انتخاب او در نتیجه پیشرفت فنشناسانه چه تغییری میکند.
تحول فناوری استاندارد زندگی آنجلا را بالا میبرد: او را قادر میکند که کارایی بیشتری داشته باشد. بیاد داشته باشید که در شکل ۳.۱۴ هم مصرف غله و هم مصرف زمان آزاد خود را بالا میبرد.
مهم است تشخیص دهیم که این تنها یکی از نتایج ممکن است. اگر منحنیهای بیتفاوتی یا مرز مقرون بهصرفهگی را بهشکل متفاوتی رسم کرده بودیم، بدهبستانهایی که پیشروی آنجلا قرار میگرفت هم متفاوت بود. میتوانیم بگوییم که پیشرفت در فناوری میتواند هم مصرف غله بیشتر و هم زمان آزاد بیشتر را مقرون بهصرفه کند، اما اینکه آنجلا مقدار بیشتر این دو را انتخاب کند بسته به ترجیحات او میان این دو کالا و نیز تمایل او به جایگزین کردن یکی با دیگری است.
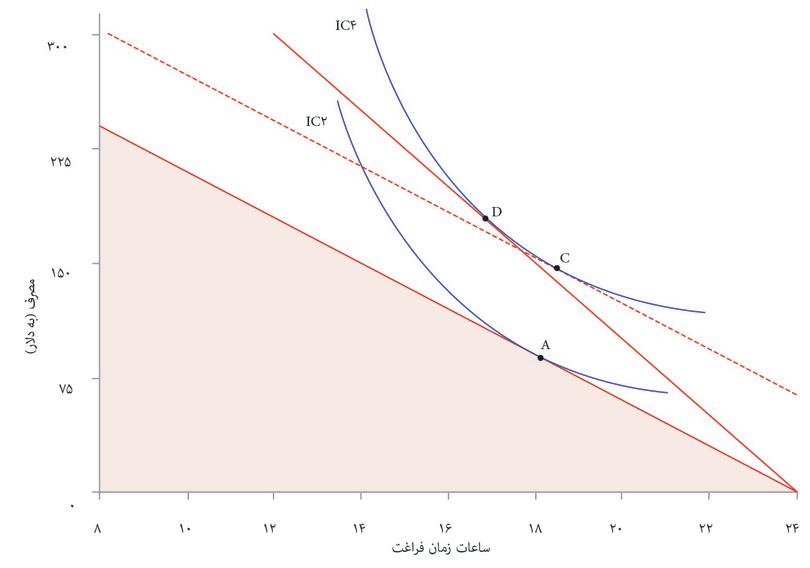
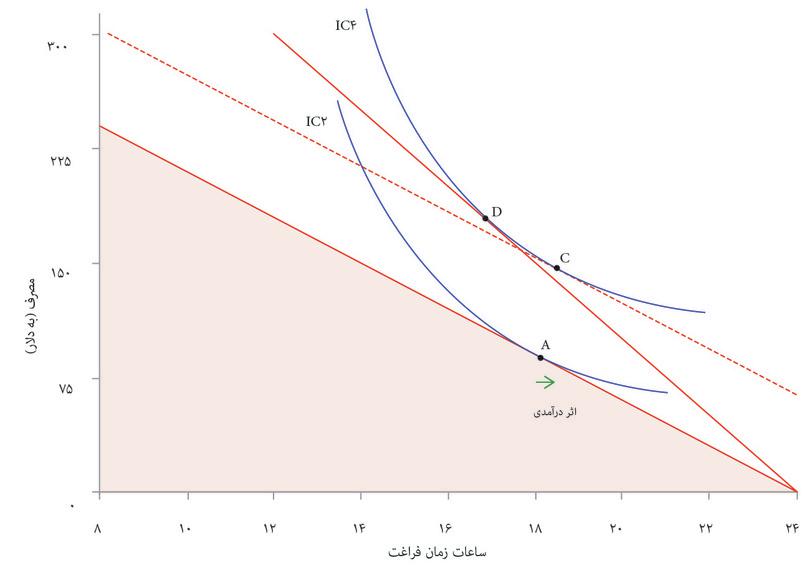
برای اینکه بفهمیم چرا، بیاد بیاورید که تغییر فناوری شیب بیشتری به تابع تولید میدهد: یعنی محصول نهایی نیروی کار آنجلا را بالا میبرد. این بدان معناست که هزینه فرصت زمان آزاد بیشتر است، و مشوق بیشتری برای کار به او میدهد. اما همچنین، حالا که میتواند غله بیشتری به ازای هر مقدار از زمان آزاد داشته باشد، ممکن است تمایل بیشتری هم داشته باشد که مقداری غله را برای زمان آزاد بیشتر از دست بدهد: یعنی ساعات کاریاش را کاهش دهد.
این دو تأثیر پیشرفت فناوری در دو سمت و سوی متضاد عمل میکنند. در شکل ۳.۱۴ تأثیر دوم است که غالب است و او نقطه E را انتخاب میکند که هم زمان آزاد بیشتری دارد و هم غله بیشتری. در بخش بعد نگاه دقیقتری به این دو سمتوسوی متضاد خواهیم داشت، و برای باز کردن آنها مثال متفاوتی را بکار خواهیم برد.
پرسش ۳.۹ (همه پاسخهای صحیح را انتخاب کنید)
شکلهای زیر تابع تولید الکسی را و مرز مقرون به صرفگی متناظر با آن برای نمره نهایی و ساعات کار یا زمان آزاد در هر روز را نشان میدهند. این اشکال تأثیر یک نوع پیشرفت در تکنیک مطالعه او را نشان میدهند که از نوسان رو به بالای دو منحنی معلوم میشود.
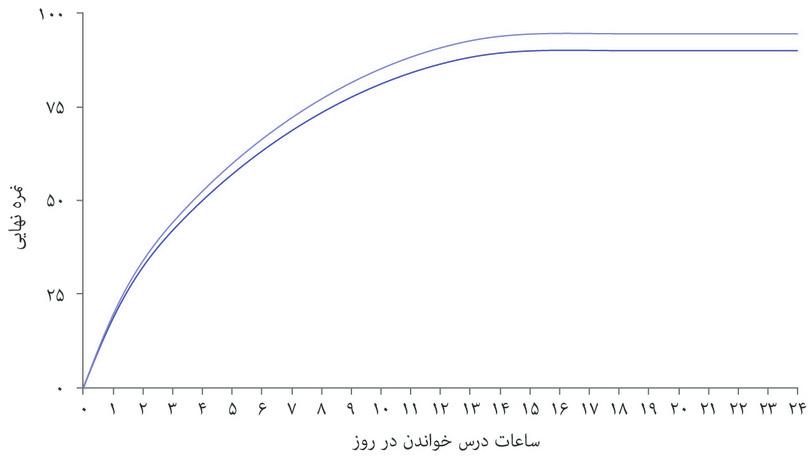
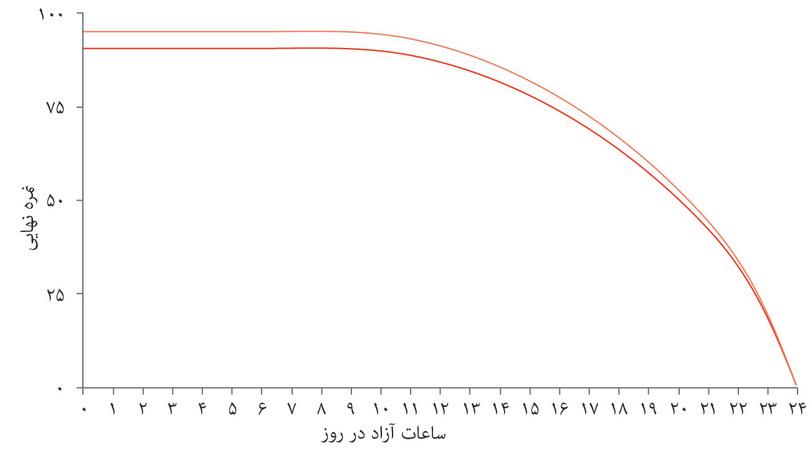
حالا به تأثیر دو مورد از تغییرات دیگر در محیط مطالعه الکسی توجه کنید:
مورد الف. الکسی به یکباره متوجه میشود که مجبور است ۴ ساعت در روز را به مراقبت از یک عضو خانواده اختصاص دهد. (ممکن است تصور کنید که محصول نهایی نیروی کار او در ساعاتی که به مطالعه میپردازد دستنخورده میماند).
مورد ب. به دلایلی مربوط به وضع سلامتش، محصول نهایی نیروی کار او برای کلیه ساعتها به میزان ۱۰ درصد کاهش پیدا میکند.
آنگاه:
- (الف) محصول نهایی نیروی کار الکسی تغییری نمیکند و بنابراین تابع تولید ثابت باقی میماند: هر تعداد ساعت کارشده همان میزان نمرهای را در پی دارد که قبلاً داشت.
- (ب) مرز مقرون به صرفگی به سمت چپ جابجا میشود و با نقطه ۲۰ ساعت روی محور افقی تقاطع پیدا میکند، چراکه حالا ۴ ساعت در روز صرف مراقبت میشود، بطوریکه هر تعداد ساعت اختصاص یافته با زمان آزاد در روز، معادل ساعات کارشده کمتر و نمره کمتری است.
- (ج) با کاهش محصول نهایی نیروی کار الکسی، منحنی تابع تولید تختتر میشود. این باعث میشود که منحنی به سمت داخل و بر محور نقطه شروع نوسان پیدا کند.
- (د) کاهش محصول نهایی به کسب نمرهای کمتر به ازای هر سطحی از ساعت کار (به استثنای صفر) منجر میشود، بنابراین مرز مقرون به صرفگی روی نقطه تقاطع شانه میاندازد و به سمت پائین چرخش پیدا میکند.
تمرین ۳.۷ تابع تولید شما
- چه چیزی میتواند یک پیشرفت فناورانه را در تابع تولید شما و یا دانشجویان همکلاسی شما ایجاد کند؟
- نموداری رسم کنید که نشان دهد چگونه این پیشرفت بر مجموعه مقرون بهصرفهگی نمرات و ساعات مطالعه شما تأثیر بگذارد.
- تحلیل کنید که چه اتفاقی ممکن است برای گزینه انتخابی شما در ساعات مطالعه، و برای انتخابهای همکلاسیهایتان بیفتد.
۳.۷ تأثیرات درآمدی و جانشینی بر تعداد ساعات کار و زمان آزاد
تصور کنید که پس از فارغالتحصیلی دنبال کار میگردید. انتظار دارید که بتوانید دستمزدی برابر با ۱۵ دلار در ساعت بدست بیاورید. شغلها برحسب تعداد ساعتی که باید کار کنید متفاوت هستند – پس باید بدانید که تعداد ساعت کاری ایدهآل شما چقدر است؟ دستمزد و ساعت کار، روی هم رفته، تعداد ساعت زمان آزادی که خواهید داشت و کل عوایدتان را تعیین میکنند.
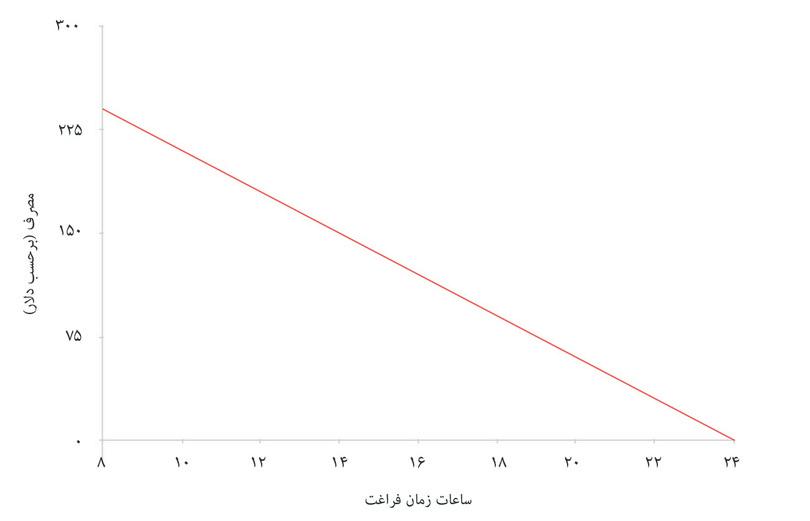
ما براساس میانگین زمان آزاد و مصرف روزانه پیش خواهیم رفت، درست مثل مورد آنجلا. تصور خواهیم کرد که هزینهکرد شما – یعنی میانگین مصرف غذا، مسکن، و سایر کالاها و خدمات – نمیتواند از کل عایدی شما بیشتر باشد (مثلاً امکان قرضگرفتن برای افزایش مصرفتان را نخواهید داشت). اگر بجای دستمزد از w استفاده کنیم، و شما tساعت زمان آزاد در روز داشته باشید و بنابراین زمان کار شما عبارت باشد از (۲۴ − t)ساعت، آنگاه حداکثر سطح مصرف شما یعنی cعبارت خواهد بود از:
- محدودیت بودجه
- یک معادله که نشان دهنده ترکیب کالاها و خدماتی است که یک فرد میتواند بهدست آورد و منابع بودجه را را به اتمام برساند.
این را محدودیت بودجه شما خواهیم نامید، زیرا نشانگر این است که از عهده خریدن چه چیزهایی برمیآیید.
در جدول شکل ۳.۱۵ زمان آزاد به ازای ساعات کار که بین صفر تا ۱۶ ساعت در روز متغیر است، و همچنین حداکثر مصرف را در شرایطی که دستمزد شما برابر ۱۵ دلار است w = $۱۵، محاسبه کردهایم.
شکل ۳.۱۵ دو کالا در این مسأله را نشان میدهد: ساعات زمان آزاد (t) روی محور افقی، و مصرف (c) روی محور عمودی. وقتی نقاط نشان داده شده در جدول را ترسیم میکنیم، به یک خط مستقیم با شیب رو به پایین میرسیم: این نمودار هندسی محدودیت بودجه است. معادله محدودیت بودجه بدین قرار است:
شیب محدودیت بودجه با دستمزد مرتبط است: به ازای هر ساعت زمان آزاد اضافی، مصرف باید به اندازه ۱۵ درصد کاهش پیدا کند. منطقه زیرین محدودیت بودجه، مجموعه مقرون بهصرفهگی شما است. مساله شما کاملا شبیه مسأله آنجلا است، بجز اینکه مرز مقرون بهصرفهگی شما یک خط مستقیم است. بیاد داشته باشید که برای آنجلا شیب مرز مقرون بهصرفهگی عبارت است از هم نرخ نهایی تبدیل (نرخی که براساس آن زمان آزاد را میتوان به غله تبدیل کرد) و هم هزینه فرصت یک ساعت زمان آزاد (یا غله از دست رفته). این مقادیر متغیرند چراکه محصول نهایی آنجلا با تعداد ساعات کاری او تغییر میکند. برای شما نرخ نهاییای که بتوانید زمان آزاد را به مصرف تبدیل کنید، و هزینه فرصت زمان آزاد، ثابت و برابری دستمزد شما (ارزش مطلق آن) است: که عبارت است از ۱۵ دلار برای نخستین ساعت کار، و بازهم ۱۵ دلار برای همه ساعات بعد از آن.
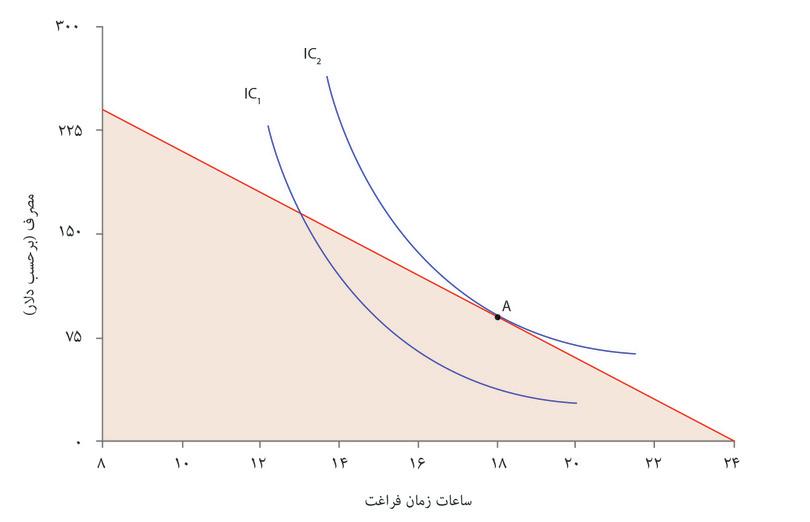
شغل ایدهآل شما چه خواهد بود؟ گزینه مرجح زمان آزاد و مصرف شما، ترکیبی روی خط مقرون به صرفهگی است که روی بالاترین منحنی بیتفاوتی ممکن باشد.
اگر منحنی بیتفاوتی شما شبیه منحنیهای شکل ۳.۱۵باشد، آنگاه شما نقطه A با ۱۸ ساعت زمان آزاد را انتخاب خواهید کرد. در این نقطه نرخ نهایی جانشینی – نرخی که شما مایلید مصرف را با زمان تعویض کنید – برابر با دستمزد (یعنی ۱۵ دلار که هزینه فرصت زمان شماست) خواهد بود. احتمالاً تمایل خواهید داشت شغلی پیدا کنید که در آن ۶ ساعت در روز کار کنید و عواید روزانه شما ۹۰ دلار خواهد بود.
شما هم مثل مورد دانشجو، درحال موازنه دو بدهبستان هستید:
| بده-بستان | نقطهای که روی نمودار قرار میگیرد | |
|---|---|---|
| MRS | نرخ نهایی جانشینی: میزان مصرفی که تمایل دارید با یک ساعت زمان آزاد مبادله کنید. | شیب منحنی بیتفاوتی |
| MRT | نرخ نهایی تبدیل: نرخ نهایی تبدیل: میزان مصرفی که میتوانید با ازدستدادن یک ساعت زمان آزاد بدست بیاورید، که با نرخ دستمزد،wبرابر است. | شیب محدودیت بودجه (مرز امکان پذیر) که برابر با دستمزد است. |
دو بدهبستان شما
شکل ۳.۱۶ دو بدهبستان شما
ترکیب بهینه مصرف و زمان آزاد شما نقطهای روی خط محدودیت بودجه است که در آن:
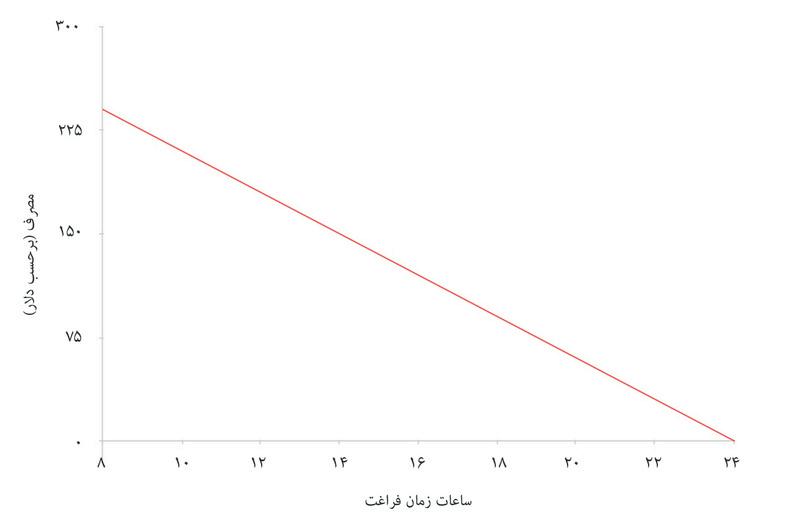
تصور کنید که درست وقتی درحال بررسی این تصمیم هستید، ایمیلی دریافت میکنید. خَیِر گمنامی مایل است که به شما یک درآمد ۵۰ دلاری در روز بدهد – آنهم بطور مادامالعمر (و تنها چیزی که از شما میخواهد اطلاعات حساب بانکیتان است). متوجه میشوید که این بر انتخاب شغلیتان تأثیر خواهد داشت. وضعیت جدید را در شکل ۳.۱۷نشان دادهایم: برای هر سطحی از زمان آزاد، کل درآمد شما (عواید بهعلاوه پاداش رازآلودی که دریافت میکنید) ۵۰ دلار بیشتر از قبل است. پس محدودیت بودجه به اندازه ۵۰ دلار به سمت بالا جابه جا شده است – مجموعه مقرون بهصرفه نیز گسترش یافته است. اکنون محدودیت بودجه شما عبارت است از:
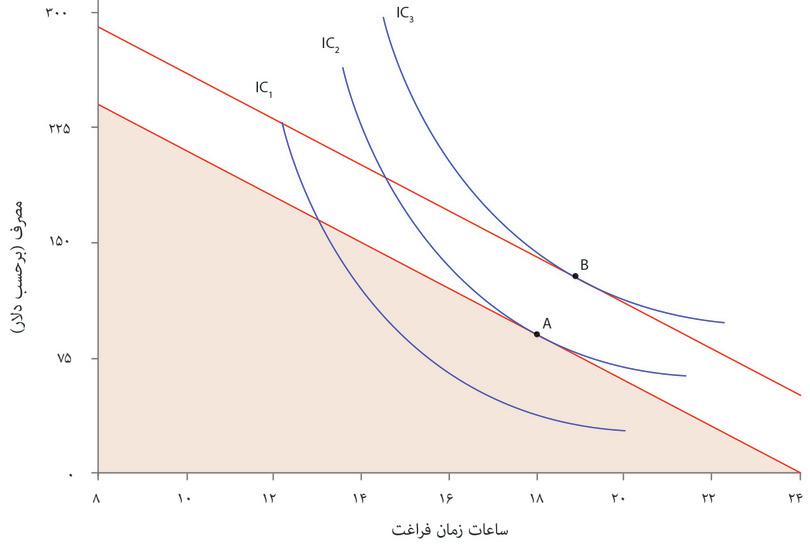
تأثیر درآمد اضافی بر انتخاب زمان آزاد و مصرف
شکل ۳.۱۷ تأثیر درآمد اضافی بر انتخاب زمان آزاد و مصرف
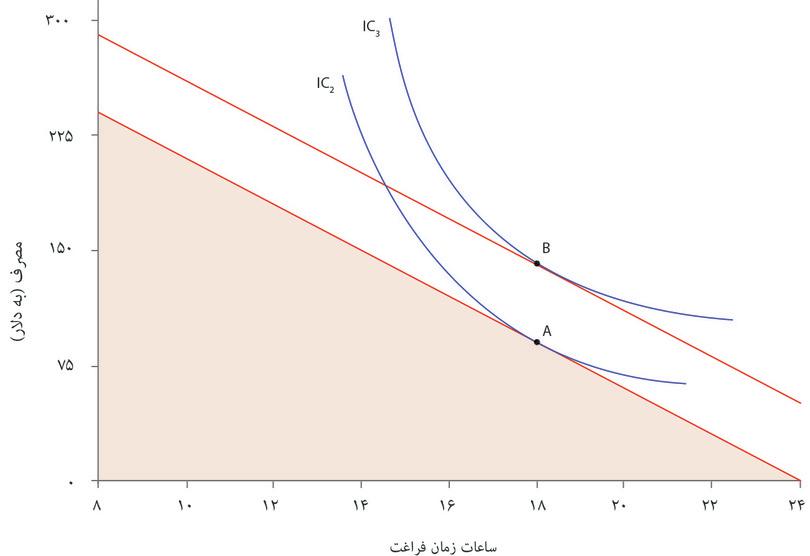
توجه داشته باشید که درآمد اضافی ۵۰ دلاری، هزینه فرصت زمان شما را تغییر نمیدهد: هر ساعت زمان آزاد همچنان مصرف شما را به اندازه ۱۵ دلار (یعنی دستمزد) کاهش میدهد. شغل ایدهآل جدید شما در نقطه B با ۱۵.۵ ساعت زمان آزاد خواهد بود. نقطه B نقطهای روی IC3 با نرخ نهایی جانشینی برابر با ۱۵ دلار است. با توجه به منحنیهای بیتفاوتی نشاندادهشده در این نمودار، پاسخ شما به درآمد اضافی صرفاً این نیست که ۵۰ دلار بیشتر خرج کنید: مصرف را به میزانی کمتر از ۵۰ دلار افزایش میدهید، و بجای آن زمان آزاد بیشتری برمیدارید. فردی دیگر با ترجیحاتی دیگر، ممکن است تمایلی به افزایش زمان آزاد خود نداشته باشد: شکل ۳.۱۸ موردی را نشان میدهد که در آن نرخ نهایی جانشینی به ازای هر مقداری از زمان آزاد، چه روی IC2 و چه روی منحنی بیتفاوتی بالاتر یعنی IC3 یکسان خواهد بود. این فرد ترجیح میدهد که زمان آزادش را ثابت نگه دارد و درعوض مصرف بیشتری داشته باشد.
تأثیر درآمد اضافی برای فردی که نرخ نهایی جانشینی او با افرایش مصرف تغییری نمیکند.
شکل ۳.۱۸ تأثیر درآمد اضافی برای فردی که نرخ نهایی جانشینی او با افرایش مصرف تغییری نمیکند.
- تأثیر درآمدی
- تأثیری است که درآمدِ اضافی، وقتی هیچ تغییری در قیمت یا هزینهی فرصت وجود نداشته باشد، ایجاد خواهد کرد.
تأثیر درآمد اضافی (کسبنشده) بر انتخاب زمان آزاد را تأثیر درآمدی مینامیم. تأثیر درآمدی که در شکل ۳.۱۷ نشان داده شد، تأثیری مثبت است – چراکه درآمد اضافی انتخاب زمان آزاد را افزایش میدهد. برای فرد موردبحث در شکل ۳.۱۸، تأثیر درآمدی صفر است، اما منفی نیست: یعنی اگر درآمد شما افزایش پیدا کرد، انتخاب شما این نخواهد بود که میزان کمتری از چیزی که برای آن ارزش قائلید داشته باشید.
به ناگهان متوجه میشوید که دادن اطلاعات حساب بانکی به این شخص ناشناس کار عاقلانهای نخواهد بود (شاید یک طعمه باشد). با حسرت تمام به برنامه اول برمیگردید و شغلی پیدا میکنید که به ۶ ساعت کار در روز نیاز دارد. یک سال بعد، بختتان یاری میکند: کارفرمایتان یک افزایش ۱۰ دلاری در ساعت و امکان مذاکره مجدد بر سر ساعات کاریتان را به شما پیشنهاد میکند. حالا محدودیت بودجه شما عبارت است از:
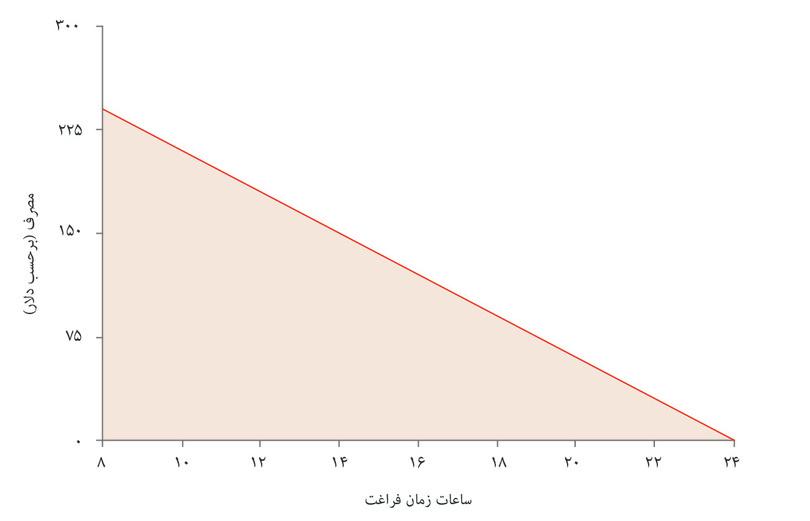
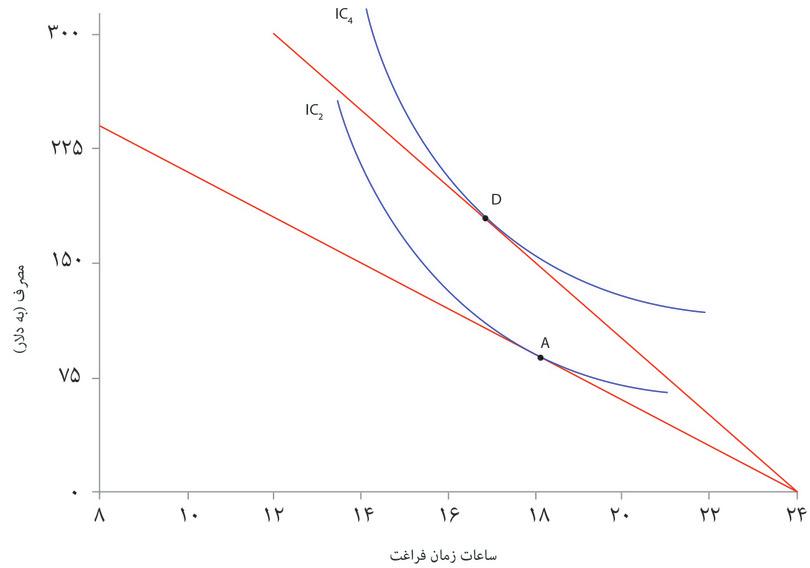
در شکل ۳.۱۹الف میتوانید ببینید که چگونه محدودیت بودجه با افزایش دستمزد تغییر میکند. با ۲۴ ساعت زمان آزاد (و صفر ساعت کار)، مصرف شما، صرف نظر از میزان دستمزد، صفر خواهد بود. اما برای هر ساعت زمان آزادی که از دست میدهید، حالا مصرف شما میتواند به اندازه ۲۵ دلار و نه ۱۵ دلار افزایش پیدا کند. پس خط محدودیت بودجه جدید شما، خط مستقیم پرشیبتری است که از نقاط (۲۴ و ۰) میگذرد و شیبی برابر با ۲۵- دلار دارد. مجموعه مقرون بهصرفه گسترش پیدا کرده است. و حالا بالاترین کارایی ممکن را در نقطه D بدست میآورید که تنها ۱۷ ساعت زمان آزاد دارد. پس از کارفرمایتان میپرسید که آیا میتوانید ساعات بیشتری کار کنید – یعنی یک روز ۷ ساعته.
شکل ۳.۱۹الف تأثیر افزایش درآمد بر زمان آزاد و مصرف
نتایج شکل ۳.۱۷و شکل ۳.۱۹ الف را مقایسه کنید. با افزایش درآمد غیرکسبشده، تمایل پیدا میکنید که ساعات کمتری کار کنید، این در حالی است که افرایش درآمدی در شکل ۳.۱۹ الف باعث میشود که تصمیم بگیرید ساعات کاریتان را افزایش دهید. چرا چنین اتفاقی میافتد؟ زیرا افزایش درآمدی دو تأثیر برجای میگذارد:
- درآمد بیشتر به ازای هر ساعت کارشده: به ازای هر سطحی از زمان آزاد میتوانید مصرف بیشتری داشته باشید و نرخ نهایی جانشینی شما بالاتر است: حالا بیشتر تمایل دارید که مصرف را قربانی زمان آزاد بیشتر کنید. این همان اثر درآمدیای است که در شکل ۳.۱۷ دیدیم – یعنی درآمد اضافی را با برداشتن زمان آزاد بیشتر و افزایش مصرف پاسخ میدهید.
- اثرِ جانشینی
- تأثیری است که با توجه به سطحِ مطلوبیتِ جدید، تنها ناشی از تغییر در قیمت یا هزینه فرصت است.
- خط محدودیت بودجه پرشیبتر است: هزینه فرصت زمان آزاد حالا بالاتر است. بهعبارت دیگر، نرخ نهاییای که میتوانید زمان آزاد را به درآمد تبدیل کنید (نرخ نهایی تبدیل) افزایش پیدا کرده است. و این بدین معناست که مشوقی برای کار بیشتر – و کاستن از زمان آزادتان- دارید. این را اثرِ جانشینی مینامیم.
Leibniz: Mathematics of income and substitution effects
اثر جانشینی بیان این ایده است که وقتی یک کالا نسبت به کالای دیگر گرانتر میشود، انتخاب شما این است که مقداری از کالای دیگر را جایگزین آن کنید. این همان اثری است که یک تغییر در هزینه فرصت، در سطح معینی از کارایی، بر خود آن فرصت خواهد داشت.
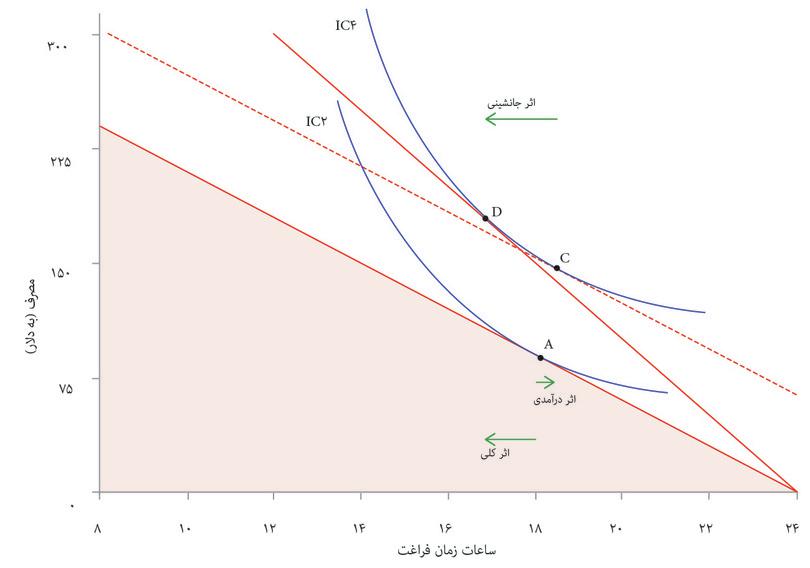
میتوانیم هردوی این تاثیرات را روی نمودار نشان دهیم. قبل از افزایش دستمزد شما در نقطه A روی IC2 هستید. دستمزد بالاتر شما را قادر میکند به نقطه D روی IC4 برسید. شکل ۳.۱۹ ب نشان میدهد که چگونه میتوانیم تغییر از نقطه A به D را به دو بخش متناظر با این دو تغییر تجزیه کنیم.
اثر درآمدی و جانشینی
یک افزایش درآمدی:
- درآمد شما را در هر سطحی از زمان آزاد افزایش میدهد، و سطح کارایی قابلحصول برای شما را بالا میبرد.
- هزینه فرصت زمان آزاد را افزایش میدهد.
و بنابراین دو تأثیر بر انتخاب زمان آزاد شما برجای میگذارد:
- اثر درآمدی (چراکه خط محدودیت بودجه به سمت بیرون حرکت میکند): و این تأثیری است که افزایش درآمدی، درصورتی که تغییری در هزینهی فرصت رخ ندهد، خواهد داشت.
- اثر جانشینی (چراکه شیب خط محدودیت بودجه، یا نرخ نهایی تبدیل، افزایش پیدا میکند): تأثیر تغییر در هزینه فرصت با توجه به سطح تازهی کارایی.
میتوانید در شکل ۳.۱۹ب ببینید که با وجود منحنیهای بیتفاوتیای با این شکل نوعی، اثر درآمدی همواره منفی خواهد بود: با هزینه فرصت بالاتر زمان آزاد، نقطهای روی منحنی بیتفاوتی را انتخاب خواهید کرد که نرخ نهایی جانشینی بالاتری دارد، که نقطهای با زمان آزاد کمتر (و مصرف بیشتر) است. تأثیر کلی افزایش دستمزد به حاصلجمع اثرات درآمدی و جانشینی بستگی خواهد داشت. در شکل ۳.۱۹ب اثر جانشینی منفی بزرگتر از اثر درآمدی مثبت است، و بنابراین زمان آزاد کمتر میشود.
پیشرفت فناوری
اگر برگردید و به بخش ۳.۶ نگاه کنید، خواهید دید که پاسخ آنجلا به افزایش بهرهوری، تابع این دو اثر متضاد هم بوده است: مشوق بیشتر برای کار محصول افزایش هزینه فرصت زمان آزاد بوده، و میل بیشتر به زمان آزاد وقتی درآمد او افزایش پیدا میکند.
ما الگوی کشاورز خودکفا را برای این بکار بردیم که ببینیم تغییر فنشناختی چگونه بر ساعات کاری اثر میگذارد. آنجلا میتواند مستقیماً به افزایش بهرهوری ناشی از ورود فناوری جدید پاسخ دهد. کارکنان هم در نتیحه تحول فناوری بهرهوری بیشتری پیدا میکنند و اگر قدرت چانهزنی کافی داشته باشند، دستمزدشان افزایش خواهد یافت. الگوی این بخش پیشبینی میکند که اگر چنین اتفاقی بیفتد، پیشرفت فناوری همچنین در میزان زمانی که کارکنان مایلاند به کار اختصاص دهند نیز تغییری به بار خواهد آورد.
اثر درآمدی دستمزد بیشتر، باعث میشود که کارگران زمان آزاد بیشتری بخواهند، درحالی که اثر جانشینی مشوقی درجهت کار کردن برای ساعات بیشتر فراهم میکند. اگر اثر درآمدی بر اثر جانشینی غالب باشد، کارگران ساعات کاری کمتر را ترجیح خواهند داد.
پرسش ۳.۱۰ (همه پاسخهای صحیح را انتخاب کنید)
شکل ۳.۱۵ خط محدودیت بودجه را در زمانی که دستمزد ساعتی ۱۵ دلار است نشان میدهد.
کدامیک از گزینههای زیر صحیحاند؟
- (الف) به ازای هر یک ساعت زمان آزادِ اضافی، ۱۵ دلار کمتر برای خرجکردن در حوزه مصرف خواهید داشت و بنابراین شیبِ خط محدودیت بودجه ۱۵- است.
- (ب) خط محدودیت بودجه، مرز مقرون به صرفگیِ ترکیبات موجود از زمان آزاد و مصرف است. شیبِ ان ثابت است و بنابراین نرخ نهایی تبدیل هم ثابت است.
- (ج) افزایش نرخ دستمزد خط محدودیت بودجه، که محور چرخش آن نقطه تقاطع روی محور x است، را پرشیبتر خواهد کرد، همانطور که هر ساعت زمان آزاد حالا هزینهی بیشتری به لحاظ مصرف از دست رفته خواهد داشت.
- (د) هر پاداشی خط محدودیت بودجه را، به موازاتِ مصرف مصرفکننده در هر سطح معلومی از زمان آزاد، رو به بیرون حرکت خواهد داد.
۳.۸ آیا این الگوی مناسبی هست؟
تااینجا ما سه بستر مختلفی که در آن انسانها برای طول زمان کاریشان تصمیم میگیرند را بررسی کردهایم – یک دانشجو (الکسی)، یک کشاورز (آنجلا)، و یک دستمزد-بگیر (که امیدواریم در آینده شما باشید). در هر مورد ترجیحات و مجموعه مقرون به صرفهگی آنها را الگوسازی کردهایم، و الگوها به ما میگویند که بهترین گزینه آنها (یعنی با حداکثر کارایی) سطحی از ساعت کاری است که در آن شیب خط مقرون بهصرفهگی با شیب منحنی بیتفاوتی برابر است.
ممکن است با خود فکر کرده باشید: اما مردم این کار را نمیکنند!
میلیاردها انسان زندگی کاری خود را بیآنکه چیزی از نرخ نهایی جانشینی و نرخ نهایی تبدیل بدانند تنظیم میکنند (اگر هم تصمیماتشان را به این شکل میگرفتند، آنوقت باید تعداد ساعاتی را که برای این محاسبات میگذارند کسر میکردیم). و حتی اگر تصمیماتشان را با استفاده از ریاضیات میگرفتند، بسیاری از ما نمیتوانستیم هر زمانی که دلمان خواست کار را ترک کنیم. پس چطور این الگو میتواند مفید باشد؟
بیاد بیاورید که در فصل دوم میگفتیم الگوها به ما کمک میکنند تا «با نگاه کردن به کمترینها، بیشترینها را ببینیم». فقدان واقعنگری یکی از ویژگیهای عامدانه این الگو است، و نه نقص آن.
آزمون و خطا به جای محاسبه
آیا الگویی که شیوه اندیشیدن ما را نادیده میگیرد، میتواند الگوی خوبی برای نحوه انتخاب ما باشد؟
میلتون فریدمنِ اقتصاددان، توضیح میداد که وقتی اقتصاددانان به این شکل از الگوها استفاده میکنند، مدعی نیستند که ما در هر نوبتی که تصمیمی میگیریم، درواقع ازطریق محاسبات این چنینی (مثلاً برابری MRS و MRT) میاندیشیم و فکر میکنیم. بلکه هرکدام از ما گزینههای مختلفی را آزمون میکنیم (و گاهی نه حتی آگاهانه) و تمایل داریم گزینههایی را انتخاب کنیم که به ما احساس رضایت درباره تصمیماتمان میدهند و نه حسرت چنانکه عادتها و محاسبههای سرانگشتی.
او در کتاب خود موسوم به مقالاتی در اقتصاد ایجابی، این مسأله را به بازی بیلیارد تشبیه میکند:
«مسأله پیشبینی ضربات یک بازیکن ماهر بیلیارد را در نظر بگیرید. ظاهراً هیچ غیرمنطقی نیست که پیشبینیهای عالی اغلب از این فرضیه ناشی میشوند که بازیکن بیلیارد ضرباتش را طوری انتخاب میکند که انگار از فرمولهای ریاضی پیچیده برای تعیین بهینهترین مسیرهای حرکت توپ خبر دارند و میتوانند زوایا را با چشمشان بهشکل دقیق تخمین بزنند و غیره؛ یا با توصیف موقعیت توپها، قادرند محاسبات بسیار سریعی از روی فرمولها انجام دهند و سپس توپها را در مسیری که فرمولها معین میکنند به حرکت درآورند.
اعتماد ما به این فرضیه بر مبنای این باور نیست که بازیکنان بیلیارد، حتی ماهرترینهایشان، قادرند از این فرآیند عبور کنند یا چنین کاری میکنند. بلکه مبتنی بر این باور است که آنها درواقع بیلیاردبازهای ماهری نخواهند بود مگر اینکه به هر حال به شیوهای توانسته باشند به این نتیجهی اساساً یکسان برسند».4
بههمین شیوه، اگر شخصی را میبینیم که منظماً بعد از کلاس درس رفتن به کتابخانه را بجای بیرون رفتن انتخاب میکند، یا زمان کار چندانی را در مزرعهاش صرف نمیکند، و یا بعد از افزایش دستمزد تقاضای ساعت کار بیشتری دارد، لازم نیست که فکر کنیم آن شخص چنین محاسباتی را انجام داده است. اگر آن شخص بعداً از انتخابش پشیمان بود، دفعهی بعد باید کمی بیشتر بیرون برود، بیشتر روی مزرعه کار کند، یا ساعات کارش را دوباره کوتاهتر کند. نهایتاً میتوانیم تصور کنیم که آنها در پایان به تصمیماتی درباره زمان کارشان برسند که به نتایج محاسبات ما نزدیک است.
به همین دلیل است که نظریه اقتصادی میتواند کمک کند که رفتارهای انسانها را تبیین و گاهی حتی پیشبینی کنیم – حتی اگر این انسانها محاسبات ریاضیاتیای که اقتصاددانها در الگوهایشان انجام میدهند را انجام نداده باشند.
تأثیر فرهنگ و سیاست
دومین وجه غیرواقعگرایانه الگو: ساعات کاری را عموماً کارفرمایان انتخاب میکنند و نه فرد کارگر، و اغلب اینطور است که کارفرما روز کاری طولانیتری نسبت به آنچه کارگران ترجیح میدهند را انتخاب میکنند. در نتیجه تعداد ساعت کاری بسیاری از مردم را قانون تنظیم میکند بطوریکه نه کارفرما و نه کارگر بالاتر از یک میزان حداکثری نمیتوانند کار کنند. در این مورد دولت مجموعه مقرون بهصرفه ساعات کار و کالا را محدود و معین کرده است.
اگرچه افراد کارگر غالباً آزادی کمی در انتخاب ساعات کارشان دارند، با این حال ممکن است در مواردی، تعداد ساعات کاری در طول زمان، و تفاوت میان کشورها، تاحدی بازتاب انتخابهای کارگران باشد. اگر تعداد زیادی از افراد کارگر در یک دموکراسی بخواهند تعداد ساعات کاریشان را کم کنند، ممکن است این را بطور غیرمستقیم و بعنوان رأیدهنده «انتخاب کنند» و نه بصورت فردی و بهعنوان کارگر. یا ممکن است بعنوان اعضای یک اتحادیه کارگری به دنبال چانهزنی برای قراردادهایی باشند که کارفرما را ملزم میکند تا برای ساعات اضافی نرخ اضافهکار بیشتری پرداخت کند.
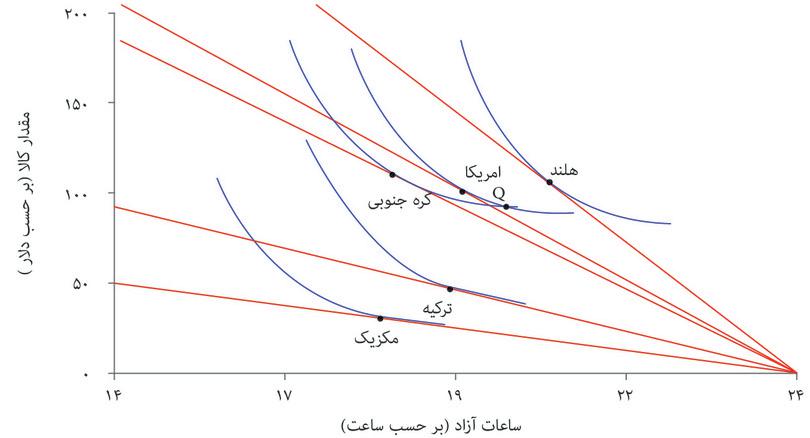
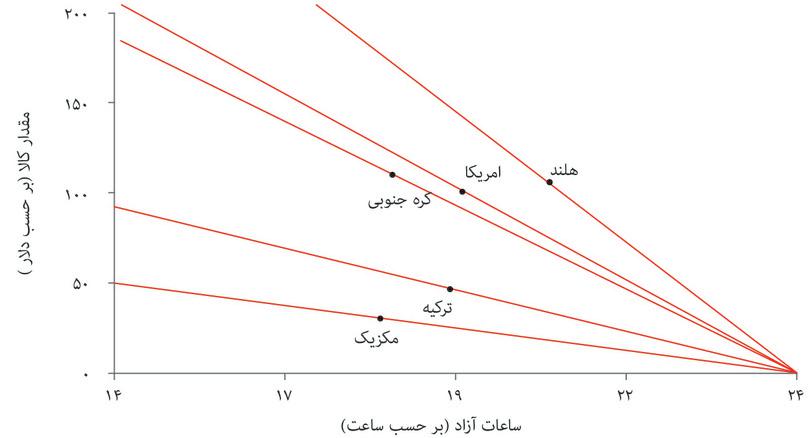
این تبیینی است که تأکید آن بر فرهنگ (به معنای تغییر ترجیحات یا تفاوت در ترجیحات میان کشورها) و سیاست (به معنای تفاوت در قوانین، یا قدرت و اهداف اتحادیههای صنفی) است. قطعاً این عوامل در توضیح تفاوت ساعات کاری میان کشورها موثرند:
بنظر میرسد که فرهنگها با یکدیگر متفاوتاند. برخی فرهنگهای اروپای شمالی به اوقات تعطیلاتشان بهای زیادی میدهند، درحالی که کره جنوبی به ساعات کاری طولانیای که خود کارکنان پیشنهاد میدهند مشهورند. محدودیتهای قانونی بر ساعت کاری هم متفاوت است. در بلژیک و فرانسه هفته کاری معمول محدود به ۳۵ تا ۳۹ ساعت است درحالی که در مکزیک این حد ۴۸ ساعت و در کنیا از این هم بیشتر است.
اما حتی در سطح فردی نیز ممکن است ما بتوانیم بر ساعات کاری تأثیر بگذاریم. برای مثال کارفرمایانی که مشاغلی با ساعت کاری مطلوب اغلب مردم را آگهی میکنند ممکن است ببینند که نسبت به کارفرمایان دیگری که ساعت کاری بسیار بیشتر (یا کمتری) ارائه میکنند، متقاضیان بیشتری دارند.
بیاد داشته باشیم که ما کیفیت یک الگو را نیز براین اساس قضاوت میکنیم که آیا بینشی درباب آنچه میخواهیم بفهمیم به ما میدهد یا نه. در فصل بعدی به این مسأله خواهیم پرداخت که آیا الگوی انتخاب ساعات کاری میتواند به ما کمک کند که بفهمیم چرا ساعات کاری تااین حد از کشوری به کشور دیگر متفاوت است و چرا، همانطور که در مقدمه دیدیم، در طول زمان تغییر کردهاند.
تمرین ۳.۸ تعریف دیگری از علم اقتصاد
لیونل رابینزی اقتصاددان در سال ۱۹۳۲ نوشت که: «اقتصاد علمی است برای مطالعه رفتار انسانی درمقام رابطهای میان اهداف معلوم و وسايل کمیاب برخوردار از کاربردهای متنوع و جایگزین».5
- مثالی از همین فصل بیاورید که نشان دهد چگونه علم اقتصاد «رفتار انسانی را بهمثابه رابطهای میان اهداف معلوم و وسایل کمیاب برخوردار از کاربردهای متنوع و جایگزین» مطالعه میکند.
- آیا «اهداف» فعالیت اقتصادی یعنی چیزهایی که به آنها تمایل داریم، ثابتاند؟ برای نشان دادن پاسختان مثالهایی از همین فصل (زمان مطالعه و نمرات، یا زمان کاری و مصرف) را بکار بگیرید.
- موضوعی که رابینز به آن اشاره میکند – داشتن بهترین عملکرد در یک وضعیت معلوم – بخشی حیاتی و لاینفک از علم اقتصاد است. اما آیا علم اقتصاد محدود به مطالعه «وسایل کمیاب برخوردار از کاربردهای متنوع و جایگزین» است؟ درپاسخدادن به این سوال، تمایز میان تعریف رابینز و تعریف دادهشده در فصل ۱ را درنظر بگیرید، و بیاد داشته باشید که رابینز این متن را در زمانی مینوشت که ۱۵ درصد از نیروی کار بریتانیا بیکار بود.
۳.۹ تبیین ساعات کار: تغییرات در طول زمان
در سال ۱۶۰۰ میانگین روزهایی که کارگر بریتانیایی سر کار بود ۲۶۶ روز بود. و این آمار تا وقوع انقلاب صنعتی تغییر چندانی نکرد. درآن زمان است که همانطور که از فصل قبل میدانیم، دستمزدها شروع به افزایش کرد و زمان کاری هم بالا رفت: تا ۳۱۸ روز در سال ۱۸۷۰.
در همین حال در ایالات متحده آمریکا ساعات کاری برای خیلی از کارگرانی که از کشاورزی به مشاغل صنعتی روی آوردند افزایش یافت. در سال ۱۸۶۵ آمریکا بردهداری را لغو کرد و بردگان سابق از آزادی خود استفاده کردند تا کمتر کار کنند. از اواخر قرن ۱۹ تا اواسط قرن ۲۰ زمان کاری در بسیاری از کشورها بهتدریج کاهش پیدا کرد. شکل ۳.۱ در ابتدای این فصل نشان میدهد که چگونه ساعات کاری سالانه از سال ۱۸۷۰ به این سو در کشورهای هلند، ایالات متحده آمریکا کاهش یافته است.6
الگوهای سادهای که ما ساختهایم مسلماً کل قضیه را بازگو نمیکنند. بیاد داشته باشید که مفروضات مبتنی بر ثابتبودن سایر شرایط (ceteris paribus) میتوانند جزئیات مهمی را از قلم بیاندازند: عواملی که در الگوها ثابت فرض میشوند، در زندگی ممکن است تغییر کنند.
همانطور که در فصل پیش توضیح دادیم، الگوی ما دو تبیین مهمی را نادیده میگرفت، که ما فرهنگ و سیاست نامیدیم. الگوی ما تبیین دیگری را فراهم میکند: اقتصاد.
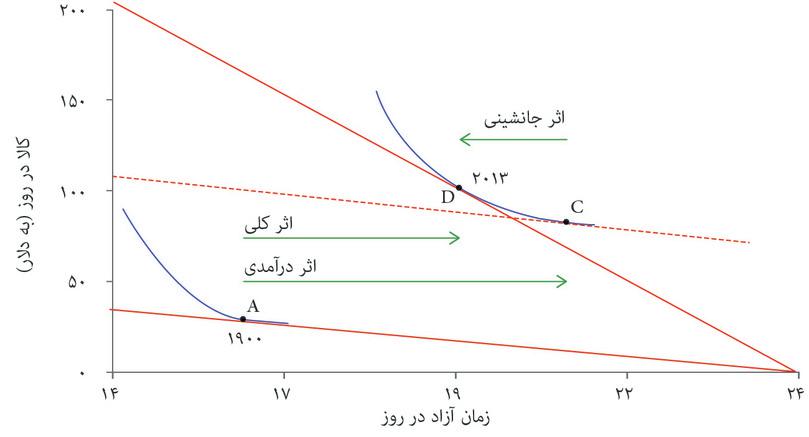
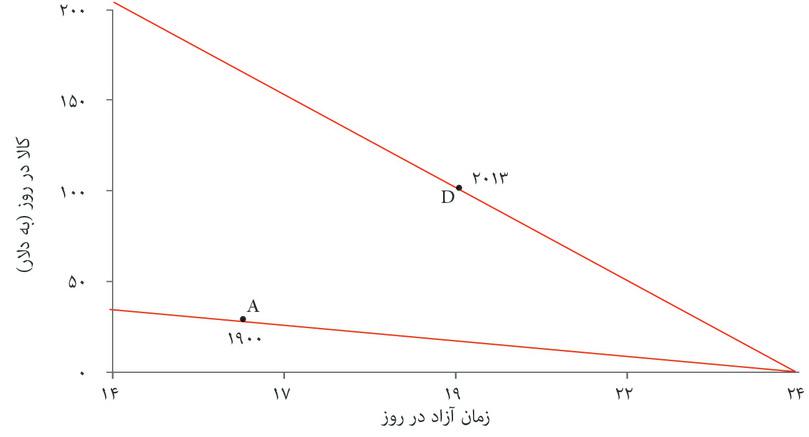
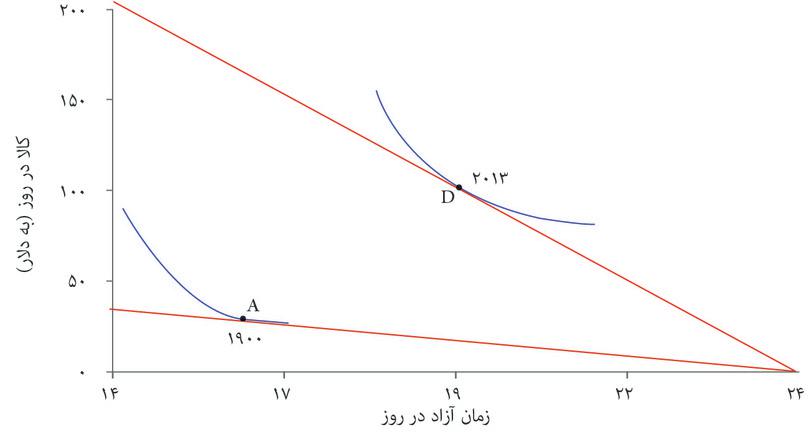
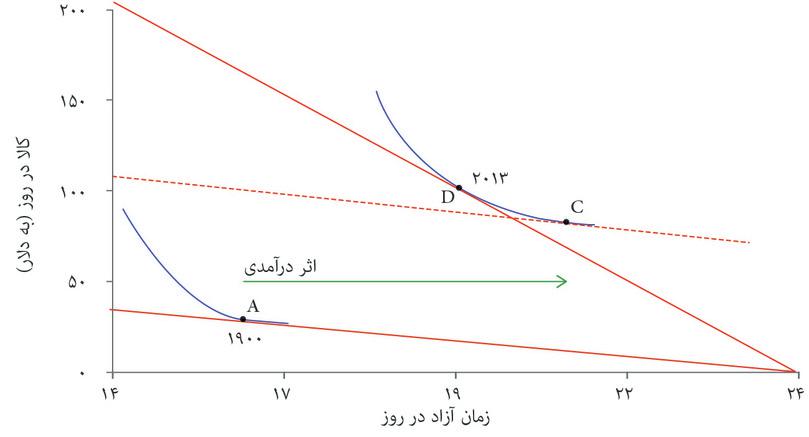
نگاه کنید به دو نقطه در شکل ۳.۲۰ که تخمینی از میانگین زمان آزاد و مقدار کالای روزانه برای هر کارگر در ایالات متحده را در سالهای ۱۹۰۰ و ۲۰۱۳ نشان میدهند. شیب منحنیهای محدودیت بودجه گذرنده از نقطههای A و D برابر با دستمزد واقعی (کالا در ساعت) در سال ۱۹۰۰ و ۲۰۱۳ است. این آن دسته از مجموعههای مقرونبهصرفهی زمان آزاد و کالا را نشان میدهد که میتوانستهاند این نقاط را ممکن کنند. سپس آن دسته از منحنیهای بیتفاوتیای که کارگران را به انتخاب این ساعات کاری واداشته را بررسی خواهیم کرد. البته ما نمیتوانیم منحنیهای بیتفاوتی را بهشکل مستقیم اندازهگیری کنیم: درباب اینکه ترجیحات کارگران با توجه به اقداماتی که کردهاند چه بوده تنها میتوانیم به بهترین حدسهایمان تکیه کنیم.
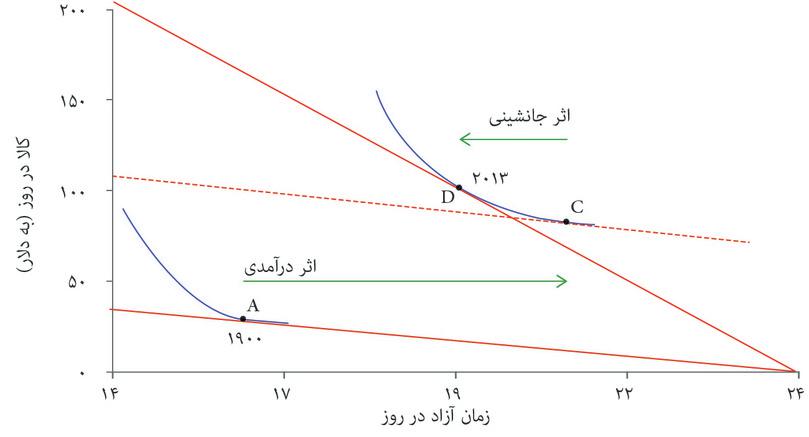
اما الگوی ما چگونه رسیدنمان از نقطه A به D را توضیح میدهد؟ ما از روی شکل ۳.۱۹ میدانیم که افزایش در دستمزد هم به یک اثر درآمدی و هم به یک اثر جانشینی منجر خواهد شد. دراین مورد اثر درآمدی بر اثر جانشینی میچربد، بطوریکه هم زمان آزاد و هم کالای مصرفشده در روز بالا میروند. به این ترتیب، شکل ۳.۲۰ صرفاً کاربست الگوی رسمشده در شکل ۳.۱۹ب به عرصه تاریخ است. با پیش رفتن طبق مراحل، اثر درآمدی و اثر جانشینی را مشاهده خواهید کرد.
اما این شیوه استدلال چگونه میتواند سایر دادههای تاریخیای که در دست داریم را توضیح دهد؟
پیش از هر چیز دوره قبل از ۱۸۷۰ در بریتانیا، یعنی زمانی که هم ساعت کاری و هم دستمزدها افزایش پیدا میکردند، را درنظر بگیرید:
- اثر درآمدی: با سطح نسبتاً پایین مصرف در دوره پیش از ۱۸۷۰، تمایل کارگران به جایگزین کردن زمان آزاد بجای کالا افزایش چندانی نداشت، آنهم در زمانی که بالارفتن دستمزد، مصرف بالاتر را ممکن میکرد.
- ثر جانشینی: اما کارگران مولدتر بودند و دستمزد بیشتری هم میگرفتند، بطوری که هر ساعت کار نسبت به گذشته پاداش بیشتری درقالب کالا میگرفت، و این مشوق برای ساعات طولانیتر کار را بیشتر میکرد.
- اثر جانشینی غلبه کرد: بنابراین قبل از ۱۸۷۰ اثر جانشینی منفی (کاهش زمان آزاد) بیشتر از اثر درآمدی مثبت (افزایش زمان آزاد) بود، پس ساعات کاری افزایش پیدا کرد.
درطول قرن بیستم شاهد افزایش دستمزدها و کاهش ساعات کاری بودیم. الگوی ما این تغییر را اینگونه توضیح میدهد:
- اثر درآمدی: تا اواخر قرن نوزدهم کارگران سطح بالاتری از مصرف داشتند و برای زمان آزاد نسبتاً ارزش بیشتری قائل بودند – نرخ نهایی جانشینی آنها بالاتر بود – بطوریکه اثر درآمدی افزایش دستمزد بزرگتر بود.
- اثر جانشینی: اثر جانشینی با دوره قبل از ۱۸۷۰ همخوانی داشت.
- اثر درآمدی اکنون غالب است: وقتی اثر درآمدی بهتدریج دست بالا را نسبت به اثر جانشینی پیدا کرد، زمان کاری کاهش پیدا کرد.
همچنین باید امکان تغییر اولویتها در طول زمان را نیز در نظر داشت. اگر با دقت به شکل ۳.۱ نگاه کنید، خواهید دید که در آخرین قسمت قرن بیستم ساعات کاری در آمریکا افزایش پیدا کرده است، اگرچه دستمزدها بهندرت افزایش داشتهاند. در همین دوره ساعات کار در سوئد هم افزایش پیدا کرده است.
تورستن وبلنِ اقتصاددان (۱۸۵۷ تا ۱۹۲۹) اصطلاح مصرف حریصانه’ را وضع کرد تا توضیح دهد که چرا مردم کمتر برخوردار به دنبال تقلید از عادات مصرفی ثروتمندان هستند.
Thorstein Veblen. 2007. Theory of the leisure class. Oxford: Oxford University Press.
- مصرف حریصانه
- خرید کالا و خدمات با هدفِ به نمایش گذاشتنِ منزلتِ اجتماعی خود برای عموم.
اما چرا؟ شاید به این دلیل که در طول این سالها آمریکا و سوئد ارزش بیشتری برای مصرف قائل بودهاند. بهعبارت دیگر، ترجیحاتشان بگونهای تغییر کرده که نرخ نهایی جانشینی شان کاهش یافته است (یعنی وضعیتی بیشتر شبیه به کارگران امروزی کره جنوبی پیدا کردهاند). این اتفاق احتمالاً میتواند به این دلیل افتاده باشد که چه در ایالات متحده و چه در سوئد سهم درآمد بدست آمده توسط ثروتمندان بهشکل قابل توجهی افزایش یافته، و عادات مصرفی اسرافکارانه ثروتمندان استاندارد بالاتری برای دیگران و همه ایجاد کرده باشد. براساس این تبیین، سوئدیها و آمریکاییها مشغول «چشمو همچشمی با اغنیا» شدهاند و ثروتمندتر شدن اغنیا همه را به سمت تغییر اولویتهایشان برده است.
آمیزهای از تأثیرات سیاسی، فرهنگی و اقتصادی بر انتخابهای ما میتواند روندهای عجیبی را ایجاد کند. در این ویدیوی اقتصاد-در-عمل، صحبتهای ژولیت شور جامعهشناس و اقتصاددان بوستون کالج را میشنوید؛ او مقالاتی درباره این تناقض نوشته است که بسیاری از ثروتمندترین افراد دنیا علیرغم عوایدی که از فناوری نصیبشان میشود بیشتر کار میکنند؛ دراینجا او میپرسد که این مسأله چه تأثیری بر کیفیت زندگی و ما بر محیط دارد؟
پرسش ۳.۱۱ پاسخهای درست را انتخاب کنید
شکل ۳.۲۰ الگویی از عرضه و مصرف نیروی کار در ایالات متحده در سال ۱۹۰۰ و ۲۰۱۳ را نشان میدهد. پیداست که نرخ دستمزدها در این فاصله زمانی افزایش پیدا کرده است.
کدامیک از گزینههای زیر صحیح است؟
- اثر جانشینی، تأثیر خالصِ تغییر در شیب خط محدودیت بودجه است. حرکت از A به D تاثیرِ ترکیبیِ حاصل از اثر جانشینی و اثر درآمدی است.
- اثر درآمدی، تاثیر درآمد بیشتر بر انتخاب زمان آزاد است که با جابجائی موازی و روبهبیرون خط محدودیت بودجه و درنتیجه جابجائی از A به C نشان داده میشود.
- با توجه به منحنیهای بیتفاوتی نشان داده شده، اثر درآمدیِ افزایش بزرگتر از اثر جانشینی است بنابراین کل زمان آزاد افزایش پیدا میکند و ساعت کار کاهش.
- با توجه به منحنیهای بیتفاوتیِ مختلف، اثر جانشینی میتوانست بر اثر درآمدی غالب شود و زمان آزاد را در فاصله سالهای ۱۹۰۰ تا ۲۰۱۳ کاهش دهد.
اما در آینده چه خواهد شد؟ اقتصادهای پر-درآمد همچنان یک استحاله اساسی را تجربه خواهند کرد: کمشدن نقش کار در طول دوره زندگی ما. عمر بیشتری خواهیم داشت، در سن بالاتری سر کار خواهیم رفت، در سنی زودتر دست از کار خواهیم کشید، و در همان سالهای کاری هم ساعتهای کمتری کار خواهیم کرد. رابرت فوگل، مورخ اقتصادی، کل زمان کاری، مشتمل بر زمان ایاب و ذهاب به محل کار و همچنین کار خانگی در گذشته را بطور تخمینی محاسبه کرده است. پیشبینیهایی برای سال ۲۰۴۰ کرده و مفهومی بنام زمان بیدارباش (یا زمان تشخیص) را به این صورت تعریف کرده است: کل 24 ساعت شبانهروز منهای زمانهایی که همه ما برای انواع امورات مربوط به بقای زیستی (خوابیدن، خوردن و بهداشت شخصی) نیاز داریم. فوگل زمان فراغت را نیز به این شکل تعریف میکند: زمان بیدارباش منهای ساعات کاری.7
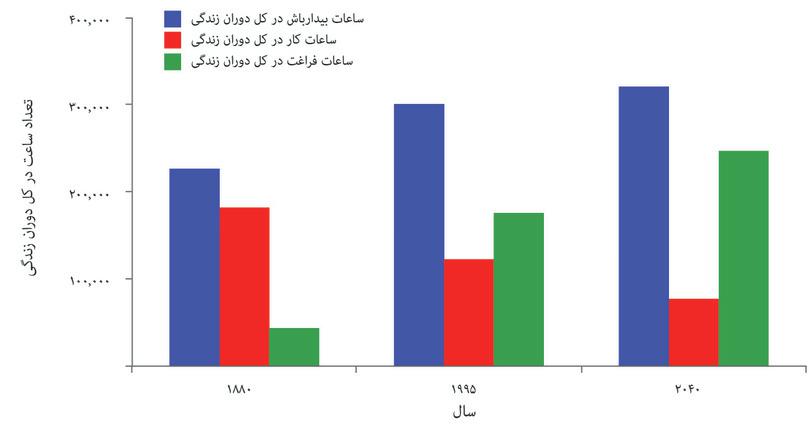
کل ساعات کار و فراغت در دوران زندگی (۱۸۸۰،۱۹۹۵،۲۰۴۰).
شکل ۳.۲۱ کل ساعات کار و فراغت در دوران زندگی (۱۸۸۰،۱۹۹۵،۲۰۴۰).
Robert William Fogel. 2000. The Fourth Great Awakening and the Future of Egalitarianism. Chicago: University of Chicago Press.
براساس تخمین او در سال ۱۸۸۰ زمان فراغت در طول زندگی تنها یکچهارم زمان کاری در طول زندگی بوده است. در سال ۱۹۹۵ زمان فراغت نسبت به زمان کار در طول کل دوران زندگی فرد بالاتر رفته است. او پیشبینی کرده که تا سال ۲۰۴۰ زمان فراغت در طول دوران زندگی سه برابر زمان کار در طول دوران زندگی خواهد بود. تخمینهای او را در شکل ۳.۲۱ ملاحظه میکنید.
ما هنوز نمیدانیم که آیا فوگل درباره کاهش زمان کار در آینده به راه اغراق رفته است، آنطور که روزی کینز رفته بود، یا نه. اما او قطعاً درست میگوید که یکی از بزرگترین تحولات ناشی از انقلاب صنعتی، کاهش گسترده نقش کار در زندگی یک فرد عادی و میانهحال بوده است.
تمرین ۳.۹ کمیابی و انتخاب
- آیا الگوهای کمیابی و انتخاب ما تبیین قابلقبولی از روندهای مشاهدهشده در ساعات کاری در طول قرن بیستم بدست میدهند یا نه؟
- چه عوامل دیگری، غیر از عوامل مورنظر در این الگو، میتوانند در تبیین آنچه رخ داده اهمیت داشته باشند؟
- این پیشبینی کینز را که تعداد ساعات کاری در قرن بیستم و پس از ۱۹۳۰ تا ۱۵ ساعت در هفته کاهش پیدا خواهد کرد، بیاد بیاورید. بنظر شما چرا تعداد ساعات کاری طبق انتظار او تغییر نکرده است؟ آیا ترجیحات مردم عوض شده است؟ تمرکز این الگو بر تعداد ساعاتی است که کارگران باید انتخاب کنند، پس به این ترتیب آیا بنظر شما بسیاری از کارکنان بیشتر از ساعاتی که دوست دارند کار میکنند؟
- کینز در مقالهاش میگفت که انسانها دو نوع نیاز یا خواسته اقتصادی دارند: نیازهای مطلقی که تابع وضعیت سایر همنوعان او نیستند، و نیازهای نسبی – یا بهعبارت دیگر چیزی که او «میل به برتری» مینامید. اصطلاح “همچشمی کردن با اغنیا” بیان ایدهی مشابهی است دال بر اینکه ترجیحات ما میتواند متأثر از مشاهدهی مصرف دیگران باشد. آیا ایده نیازهای نسبی میتواند توضیح دهد که چرا کینز تا این حد درباره ساعات کار اشتباه میکرد؟
۳.۱۰ تبیین ساعات کار: تفاوت میان کشورها
شکل ۳.۲ نشان میداد که در کشورهایی با درآمد بالاتر (برحسب سرانه جی.دی.پی) کارگران مایلند تا زمان آزاد بیشتری داشته باشند، اما این نکته را هم نشان میداد که درمیان کشورهای مختلف برخوردار از سطوح درآمدی مشابه، تفاوتهای مهمی هم بهلحاظ ساعات کاری وجود دارد. برای اینکه این تفاوتها را با الگوی خود تحلیل کنیم، به سنجه درآمدی متفاوتی نیاز داریم که تناظر دقیقتری با عواید حاصل از استخدام شغلی داشته باشد. جدول زیر تعداد ساعات کاری برای ۵ کشور را همراه با درآمد قابل استفاده یک کارمند عادی و میانهحال (برحسب مالیاتها و مزایای یک شخص واحد بدون فرزند) نشان میدهد.
از روی این ارقام، زمان آزاد سالانه، و همچنین میانگین دستمزد را (با تقسیم درآمد سالانه بر تعداد ساعات کارشده در سال) محاسبه کردهایم. در پایان هم زمان آزاد روزانه و مصرف روزانه را با تقسیم زمان آزاد و عواید سالانه بر ۳۶۵ روز محاسبه کردهایم.
| کشور | میانگین ساعت کار شده در سال هر کارمند | میانگین درآمد قابل استفاده (فرد مجرد و غیر کودک) | مانگین سالانه زمان آزاد | دستمزد (درامد قابل استفاده بر اساس یک ساعت کار) | زمان آزاد در یک روز | مصرف در روز |
|---|---|---|---|---|---|---|
| آمریکا | ۱.۷۸۹ | ۳۶.۷۳۷ | ۶.۹۷۱ | ۲۰.۵۴ | ۱۹.۱۰ | ۱۰۰.۶۵ |
| کره جنوبی | ۲.۱۶۳ | ۳۹.۶۸۶ | ۶.۵۹۷ | ۱۸.۳۵ | ۱۸.۰۷ | ۱۰۸.۷۳ |
| هلند | ۱.۳۸۳ | ۴۰.۱۷۱ | ۷.۳۷۷ | ۲۹.۰۵ | ۲۰.۲۱ | ۱۱۰.۰۶ |
| ترکیه | ۱.۸۵۵ | ۱۷.۱۱۸ | ۶.۹۰۵ | ۹.۲۳ | ۱۸.۹۲ | ۴۶.۹۰ |
| مکزیک | ۲.۲۲۶ | ۱۱.۰۴۶ | ۶.۵۳۴ | ۴.۹۶ | ۱۷.۹۰ | ۳۰.۲۶ |
زمان آزاد و مصرف روزانه در کشورهای مختلف (۲۰۱۳)
۳.۲۲ زمان آزاد و مصرف روزانه در کشورهای مختلف (۲.۱۳)
OECD. Average annual hours actually worked per worker. Accessed June 2016. Net income after taxes calculated in US dollars using PPP exchange rates.
شکل ۳.۲۳ نشان میدهد که چگونه میتوانیم از این دادهها و براساس الگوی ارائه شده در بخش ۳.۷ درجهت فهم تفاوت میان کشورها استفاده کنیم. از روی دادههای شکل ۳.۲۲ میزان مصرف و زمان آزاد روزانه برای یک کارگر نوعی در هر کشور را، و همچنین خط محدودیت بودجه را به روال سابق (یعنی با استفاده از خط (۲۴، ۰) با شیب برابر با دستمزد، محاسبه کردهایم. درباره ترجیحات کارگران در هر کشور هیچ اطلاعاتی نداریم، و نمیدانیم که ترکیبات موجود در نمودار را میتوان بهعنوان انتخاب صورتگرفته توسط خود کارگران تفسیر کنیم یا نه. اما اگر فرض کنیم که این ترکیبها واقعاً بازتاب انتخاب کارگران هستند، آنوقت میتوانیم به این بپردازیم که این دادهها درباره ترجیحات مختلف کارگران در کشورهای مختلف به ما چه میگویند.
از روی شکل ۳.۲۳ میتوانیم ببینیم که میانگین زمان آزاد در مکزیک و کره جنوبی تقریباً یکسان بوده، اگرچه میزان دستمزد در کره جنوبی بسیار بالاتر از مکزیک بوده است. مردم کره جنوبی، آمریکاییها و هلندیها مبلغ تقریباً یکسانی برای خرج کردن در هر روز دارند، بااینحال مردم کره جنوبی ۳ ساعت زمان آزاد کمتری دارند. آیا میتوان گفت که مردم کره جنوبی ترجیحات یکسانی با آمریکاییها دارند، بطوریکه اگر نرخ دستمزد در کره جنوبی افزایش پیدا کند آنها هم همین انتخاب را خواهند کرد؟ چنین چیزی محتمل بنظر نمیرسد: اثر جانشینی آنها را وادار خواهد کرد که کالای بیشتری مصرف کنند و زمان آزاد کمتری بردارند، و این فرض که تأثیر درآمدی ناشی از یک افزایش دستمزد آنها را به سمت مصرف کالای کمتر ببرد نامحتمل است. درعوض آنچه محتملتر است این فرضیه است که مردم کره جنوبی و آمریکاییها (بطور میانگین) ترجیحات متفاوتی دارند. با استفاده از خطوط جانبی، چند منحنی بیتفاوتی فرضی را که میتوانند به تبیین تفاوتهای میان کشورها کمک کنند ملاحظه کنید. توجه داشته باشید که منحنیهای بیتفاوتی ایالات متحده و کره جنوبی هم را قطع میکنند. این بدان معناست که مردم کره جنوبی و آمریکاییها ترجیحات متفاوتی دارند.
نقطه Q در آخرین مرحله شکل نقطه تقاطع دو منحنی بیتفاوتی کره جنوبی و آمریکا است. در این نقطه منحنی بیتفاوتی آمریکا شیبدارتر از منحنی بیتفاوتی کره جنوبی است. این بدان معناست که یک آمریکایی میانهحال مایل است که واحد بیشتری از کالای روزانه را در ازای یک ساعت زمان آزاد نسبت به شهروند میانهحال کره جنوبی از دست بدهد (نرخ نهایی جانشینی)، و این چیزی است که با این ایده که مردم کرهجنوبی عمیقاً سختکوش هستند، خوانایی دارد. بنابراین ممکن است درنظرگرفتن تفاوت در ترجیحات میان کشورها یا میان افراد اهمیت داشته باشد.
تمرین ۳.۱۰ ترجیحات و فرهنگ
فرض کنید که نقاط رسمشده در شکل ۳.۲۳ بازتابی باشد از انتخابهایی که کارگران این ۵ کشور، براساس الگوی ما، در مورد زمان آزاد و مصرف دارند.
- آیا ممکن است که مردم در ترکیه و در آمریکا ترجیحات مشابهی داشته باشند؟ اگر چنین است، یک افزایش دستمزدی در ترکیه چه تأثیری بر مصرف و زمان آزاد خواهد داشت؟ و این چه معنایی برای اثر درآمدی و اثر جانشینی خواهد داشت؟
- فرض کنید که مردم در ترکیه و در کره جنوبی ترجیحات یکسانی داشته باشند. در این صورت، درباره اثر درآمدی و اثر جانشینی ناشی از یک افزایش دستمزد چه میتوان گفت؟
- اگر دستمزدها در کره جنوبی افزایش پیدا کنند، آیا انتظار خواهید داشت که مصرف در این کشور نسبت به هلند بالاتر باشد یا پایینتر؟ چرا؟
تمرین ۳.۱۱ ساعات کاری در میان کشورها و زمان
جدول زیر نشان میدهد که در طول قرن بیستم چه تحولاتی در ساعات کاری در برخی کشورها اتفاق افتاده است. (مورد بریتانیا را در هر دو جدول و برای سهولت مقایسه آوردهایم).
![ساعات کاری در قرن بیستم]()
Michael Huberman and Chris Minns. 2007. ‘The times they are not changin’: Days and hours of work in Old and New Worlds, 1870–2000’. Explorations in Economic History 44 (4): pp. 538–567.
- آنچه اتفاق افتاده را چطور توصیف میکنید؟
- کشورهای واقع در دسته A چه تفاوتی با کشورهای واقع در دسته B دارند؟
- درباب اینکه افت ساعات کاری در برخی کشورها بیشتر از برخی دیگر بوده است، احتمالاً چه توضیحاتی دارید؟
- فکر میکنید چرا افت ساعات کاری در غالب کشورها در نیمه نخست قرن سریعتر بوده است؟
- در سالهای اخیر، آیا کشوری وجود دارد که در آن ساعات کار افزایش پیدا کرده باشد؟ و فکر میکنید چرا این اتفاق افتاده است؟
۳.۱۱ نتیجهگیری
ما از الگویی برای تصمیم-سازی تحت شرایط کمیابی استفاده کردیم تا انتخاب ساعات کار را تحلیل کنیم و بفهمیم چرا ساعات کاری در طول قرن گذشته افت داشته است. ترجیحات مردم در رابطه با کالا و زمان آزاد بواسطه منحنیهای بیتفاوتی توصیف میشوند، و تابع تولید افراد (یا محدودیت بودجه آنها) تعیینکننده مجموعه مقرون بهصرفهگی آنهاست. گزینهای که کارایی را به حداکثر میرساند، نقطهای روی مرز مقرون بهصرفهگی است که در آن نرخ نهایی جانشینی (MRS) میان کالا و زمان آزاد، با نرخ نهایی تبدیل (MRT) برابر است.
هر افزایشی در بهرهوری یا دستمزدها، مقدار MRT را تغییر میدهد و هزینه فرصت زمان آزاد را بالا میبرد. این مشوقی فراهم میکند که افراد ساعات بیشتری کار کنند (یعنی اثر جانشینی). اما درآمد بالاتر ممکن است میل به زمان آزاد را هم بیشتر کند (اثر درآمدی). تغییر نهایی در ساعات کار بسته به این است که کدامیک از این دو اثر بزرگتر باشد.
مفاهیم معرفیشده در فصل سوم
پیش از آنکه به فصل بعد بروید، تعاریف زیر را مرور کنید:
۳.۱۲ برای مطالعه بیشتر
-
Elizabeth Ashby Plant, Karl Anders Ericsson, Len Hill, and Kia Asberg. 2005. ‘Why study time does not predict grade point average across college students: Implications of deliberate practice for academic performance.’ Contemporary Educational Psychology 30 (1): pp. 96–116. ↩
-
John Maynard Keynes. 1963. احتمالاتِ اقتصادی برای نوادگان ما. In Essays in Persuasion, New York, NY: W. W. Norton & Co. ↩
-
Tim Harford. 2015. ‘The rewards for working hard are too big for Keynes’s vision’. The Undercover Economist. First published by The Financial Times. Updated 3 August 2015. ↩
-
Milton Friedman. 1953. Essays in positive economics, 7th ed. Chicago: University of Chicago Press. ↩
-
Lionel Robbins. 1984. An essay on the nature and significance of economic science, 3rd ed. New York: New York University Press. ↩
-
Robert Whaples. 2001. ‘Hours of work in U.S. History’ EH.Net Encyclopedia. ↩
-
Robert William Fogel. 2000. The fourth great awakening and the future of egalitarianism: The political realignment of the 1990s and the fate of egalitarianism. Chicago: University of Chicago Press. ↩