فصل ۴ تعامل اجتماعی
فهرستها و موضوعات فصلها
ترکیبی از منفعت شخصی، توجه به رفاه دیگران، و وجود نهادهای مناسب میتواند نتایج اجتماعی مطلوب را در تعامل مردم درپی داشته باشد.
- نظریهی بازی شیوهای است از درک اینکه مردم چگونه برمبنای موانع محدودگر کنشهایشان، براساس انگیزهها، و یا نظراتی که دربارهی اعمال احتمالی دیگران دارند، با یکدیگر تعامل میکنند.
- آزمایشها و دیگر شواهد نشانگر آنند که منفعت شخصی، توجه به دیگران، و تمایل به برابری، همه و همه انگیزههایی هستند که چگونگی تعامل مردم با یکدیگر را تبیین میکنند.
- در اغلب تعاملات اندکی تضاد منافع بین مردم وجود دارد، اما فرصتهایی برای سود متقابل نیز هست.
- پیگیری نفع شخصی گاها میتواند به نتایجی بیانجامد که از نظر همهی مشارکین مطلوب باشد، و گاها میتواند خروجی مطلوب هیچیک از طرفین از کار درنیاید.
- منفعت شخصی را میتوان در جهت خیر عمومی در بازار مهار کرد، اینکار با اعمال محدودیت بر کنشهای آزاد مردم به واسطهی دولتها، و وضع مجازات بر کنشهایی صورت میگیرد که خروجی بد ببار میآورند.
- توجه به دیگران و دغدغهی انصاف یا عدالت، درونیسازی تاثیرات کنشهایمان بر دیگران را برایمان میسر میسازد، و لذا میتواند در ایجاد خروجیهای اجتماعی مطلوب دخیل باشد.
«اکنون شواهد علمی چشمگیری در اینباره هست: تغییرات اقلیمی نمایانگر مخاطرات جهانی بسیار جدی است، و پاسخ جهانی عاجلی را میطلبد»1
گزارش اجرایی استرن ریویو منتشره به سال ۲۰۰۶، با این گفتهی رک و صریح آغاز میشود. وزارت دارایی بریتانیا به گروهی از اقتصاددانان و تحت سرپرستی سِر نیکلاس اِسترن (لُرد استرنِ فعلی) رییس سابق بانک جهانی ماموریت داد تا شواهد مربوط به تغییرات اقلیمی را ارزیابی کرده و برای درک الزامات و کاربستهای اقتصادی آن تلاش کنند. طبق پیشبینی استرن ریویو، عواید اقدامات اولیهی اینکار بر هزینههای آن خواهد چربید.
پنجمین گزارش ارزیابانه توسط نشست بیندولتی تغییرات اقلیمی (IPCC) نیز این نکته را تایید میکند. اقدام اولیه به معنای توقف یکباره در انتشار گازهای گلخانهای خواهد بود، که از طریق کاهش مصرف کالاهای انرژی-بر حاصل میشود، با چرخشی به سوی تکنولوژیهای متفاوت انرژی، و با بهبود کارایی تکنولوژیهای موجود.2
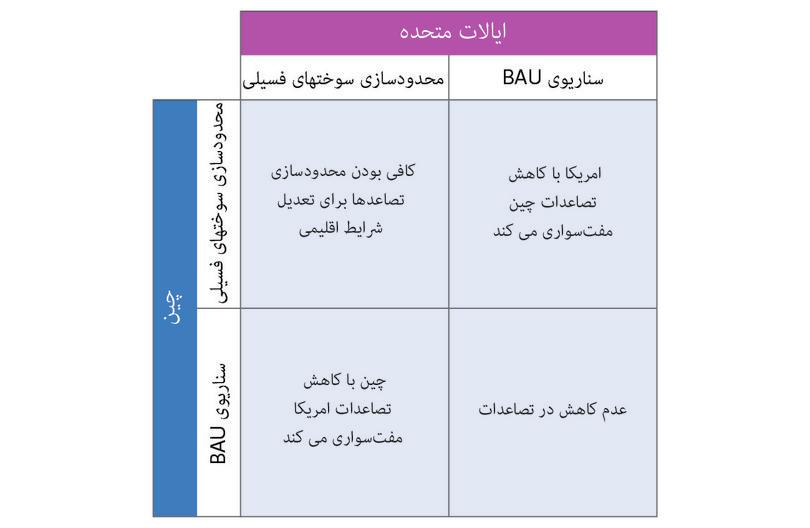
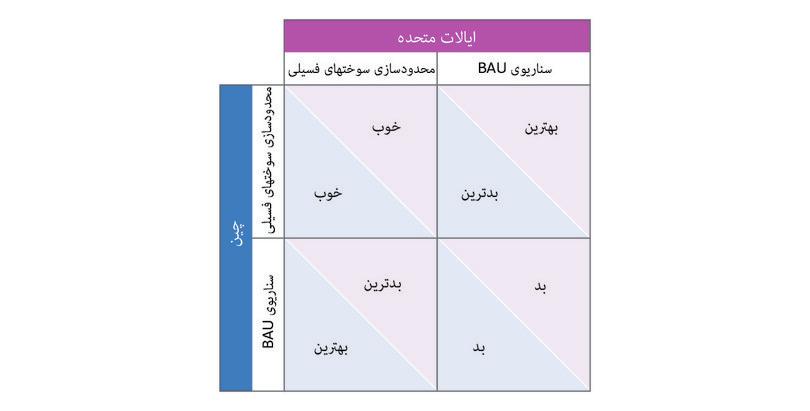
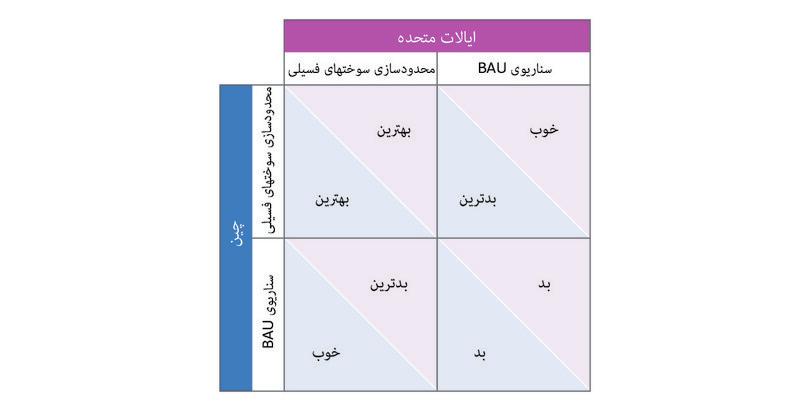
اما اگر همچنان پیگیر همانچیزی باشیم که استرن «تجارت همیشگی» مینامد هیچیک از اینها اتفاق نخواهد افتاد: سناریویی که درآن مردم، دولتها و تجارتها در پیگیری لذات، سیاست و سود خویش آزادند، بدون آنکه تاثیر کنشهای خویش بر دیگران را بهحد کافی لحاظ کنند، منجمله سرنوشت نسلهای آتی را.
دولتهای ملی برسر سیاستگذاریهای لازمه با یکدگر اختلاف دارند. بسیاری از ملل اروپایی برای نظارتهای جدی جهانی دربارهی انتشار کربن تحت فشارند، حالآنکه هند و چین، که تاثیرات مخرب اقتصادی آن بر اروپا به تکنولوژیهای زغالسوزشان بستگی داشته، در برابر چنین اقداماتی مقاومت میکنند.
- تنگناهای اجتماعی
- وضعیتی که در آن رفتارهایی که افراد مستقلاً و به دنبالِ اهدافِ شخصی خود اتخاذ کردهاند، به نتیجهای منجر میشود که نازلتر از نتیجهای است که میتوانست در صورتی که افراد بجای اینکه بعنوان فرد رفتار کنند، با یکدیگر عمل میکردند بدست آید.
[امروزه دیگر] مسالهی تغییر اقلیم مسالهای دور از ذهن و غریب نیست. بلکه نمونهای است از آنچه تنگنای اجتماعی میخوانیم. تنگناهای اجتماعی زمانی رخ میدهند که مردم به تاثیرات تصمیماتشان ـ چه مثبت و چه منفی ـ بر دیگران چندان وقعی نمینهند.
تنگناهای اجتماعی به کرات در زندگی ما رخ میدهند. ترافیک سنگین وقتی رخ میدهد که جنس انتخاب ما برای انجام کاری ـ برای مثال رفتن به سر کار با خودروی شخصی، بهجای استفاده از وسایل حمل و نقل عمومی ـ بهگونهایست که تبعات آن انتخاب و تاثیر آن بر تراکم و ترافیک خیابان را در نظر نمیگیریم. بهنحو مشابهی، استفادهی مفرط از آنتیبیوتیکها برای بیماریهای کوچک و نه چندان جدی ممکن است که به شخص بیمار کمک کند تا سریعتر بهبود یابد، اما باعث تولید باکتریهای مقاوم در برابر آنتیبیوتیک میشود که تاثیرات مضر آنها بر بسیاری از بیماران بمراتب بیشتر است.
تراژدی منابع عمومی
یک زیستشناس به نام گَرِت هاردین در سال ۱۹۶۸ در مجله ساینس مقالهای درباب تنگناهای اجتماعی منتشر میکند با عنوان تراژدی منابع عمومی. او مدعی است منابعی که در تملک هیچکس نیستند (گاهی تحت عنوان «داراییهای عمومی» یا « منابع مشترک عمومی» از آنها یاد میشود)، از قبیل اتمسفر زمین یا ذخایر ماهی، بسادگی مورد بهرهبرداری مفرط واقع میشوند، مگر اینکه دسترسی به آنها را به طرقی محدود کنیم. گروه ماهیگیران اگر اینهمه ماهی تن صید نکنند آسایش بیشتری خواهند داشت، و مصرفکنندگان هم اگر کمتر ماهی تن بخورند رفاه بیشتری خواهند داشت. به نفع بشریت است که آلایندههای کمتری انتشار دهد، اما اگر صرفاً بهعنوان یک فرد تصمیم بگیرید مصرفتان را کاهش دهید، تبعاً آلودگی کربنی یا شمار تن ماهیهایی که صید میکنید، به ندرت تأثیری بر سطوح جهانی آلودگی خواهد داشت!3
- مفتسواری
- منتفعشدن از مشارکت دیگران در یک پروژه همیارانه بدون مشارکتِ خودِ فرد
نمونه تراژدیهای هاردین و تنگناهای اجتماعی دیگر همه در اطرافمان هستند: اگر همخانهای دارید، یا باخانواده زندگی میکنید، حتما میدانید که تمیز نگهداشتن آشپزخانه یا حمام چه کار مشکلی است. هر کس خانه را تمیز کند، همه نفع میبرند، اما کار آسانی نیست. هرکسی که تمیز کند این هزینه را متقبل میشود. گاهی چنین گفته میشود که دیگران در این میان مفتسواریمیکنند. بهعنوان یک دانشجو اگر یک تکلیف گروهی انجام داده باشید، متوجهید که هزینهی تلاش( مطالعهی یک مساله، گردآوری شواهد، یا بیرونکشیدن نتایج) هزینهای فردی است، حالآنکه عواید کار( نمرهی بهتر، رتبهی بالاتر در کلاس، یا همین تشویق و تایید همکلاسیها) نصیب کل گروه میشود.4
حلوفصل تنگناهای اجتماعی
چیز جدیدی در مورد تنگناهای اجتماعی وجود ندارد؛ از دوران پیشاتاریخ تا کنون با آنها مواجه بودهایم.
- دیگرخواهی
- تمایل به متحمل شدن هزینه درقبالِ منتفع شدن فردی دیگر
بالغ بر ۲۵۰۰ سال پیش، ایزوپ، قصهگوی یونانی در حکایت زنگوله بستن به گربه، دررابطه با یک تگنای اجتماعی چیزهایی نوشت. یک گروه از موشها میخواهند که یکی از اعضایشان زنگولهای را دور گردن گربه بیاندازد. مادام که زنگوله به گردن گربه باشد، قادر به گرفتن و خوردن باقی موشها نخواهد بود؛ اما ممکن است برای موش مامور نتیجهی چندان خوشایندی نداشته باشد. 5 مثالهای بیشماری در اثنای جنگها یا بلایای طبیعی هست که افراد زندگی خود را برای دیگرانی که عضو خانواده نیستند و حتی ممکن است بالکل غریبه باشند ایثار میکنند. چنین کنشهایی را دیگرخواهانهمینامیم.
قربانی کردن دیگرخواهانهی خویش مهمترین راه جوامع برای حل تنگنا و کاهش مفتسواری نیست. برخی اوقات مسائل را میتوان با سیاستگذاریهای دولتی حل کرد. برای مثال، دولتها بهشکل موفقیتآمیزی برای جلوگیری از استفادهی بیرویه از ذخایر ماهی کاد در آتلانتیک شمالی سهمیه وضع کردهاند. در بریتانیا میزان زبالهای که به جای بازیافت در انبارهای زباله خالی میشوند، از طریق بستن مالیات بر زباله دانیها بهنحو چشمگیری کاهش یافته است.
اجتماعات محلی نیز نهادهایی برای تنظیم رفتار آفریدهاند. جوامع آبی نیازمند کار مردم برای نگهداری آبراهههایی است که کل جامعه از آن بهرهمند میشوند. افراد نیز نیازمند صرفهجویی در استفاده از آب کمیاب هستند و باز بهگونهای که محصولات دیگران ببار آیند، هرچند که این امر به محصول کوچکتر برای خودشان منجر شود. در والنسیای اسپانیا، جماعات کشاورز قرنهاست یکسری قوانین عرفی برای تنظیم اعمال اشتراکی و جلوگیری از استفادهی زیاد آب بکار میگیرند. از قرون وسطی به این سو دادگاهی برای حکمیت دارند تحت عنوان دادگاه آب Tribunal de las Aguas که اختلافات کشاورزان دربارهی اجرای قانون را رتق و فتق میکند. حکمیت این داوری محلی بلحاظ قانونی قابل اجرا نیست. قدرت آن فقط از احترام به جماعت ناشی میشود، و بااینهمه تصمیمات آن بهنحو جهانشمولی مشروع است.
- نظریهی بازی
- شاخهای از ریاضیات که به مطالعه تعاملاتِ استراتژیک میپردازد، و منظور از تعامل استراتژیک اشاره به وضعیتهایی است که در آن هر کنشگر میداند که مزایایی که دریافت میکند تابعِ کنشهایی است که همه افراد دیگر اتخاذ میکنند. همچنین نگاه کنید به: بازی
- تعاملات اجتماعی
- وضعیتهایی که در آن کنشهای اتخاذشده توسط هر فرد، بر نتایجِ حاصله برای سایر افراد و همچنین برای خود آن فرد تأثیر میگذارد.
در این فصل ابزار نظریهی بازی را برای الگوسازی تعاملات اجتماعی، بکار میگیریم، که در آنها تصمیمات افراد، هم خود آنها و هم دیگران را تحت تاثیر قرار میدهد. نگاهی خواهیم داشت به وضعیتهایی که به تنگنای اجتماعی ختم میشوند و نیز بررسی میکنیم که مردم چگونه گاهی میتوانند این تنگنا را بگشایندـ اما گاهی قادر به حل کردن آنها نیستند ( یا هنوز نیستند)، همچون مورد تغییرات اقلیمی.
اما همه تعاملات اجتماعی هم به تنگناهای اجتماعی منجر نمیشوند، حتی اگر که افراد در راستای منافع شخصی خویش کنش نشان دهند: بخش بعدی را با مثالی شروع میکنیم که در آن «دست نامرئی» بازار، طبق تعریف آدام اسمیت، منفعت شخصی را بهگونهای هدایت میکند که افراد کنشگر مستقل حتما به یک نتیجه متقابلاً سودآور بهرهمند شوند.
تمرین ۴.۱ تنگناهای اجتماعی
استفاده از سرخط خبرهای هفتهی پیش:
- دو تنگنای اجتماعی گزارش شده را مشخص کنید (سعی کنید از مثالهایی استفاده کنید که در بالا نیامدهاند).
- در هر مورد مشخص کنید که چگونه بر تعریف تنگنای اجتماعی صحه میگذارد.
۴.۱ تعامل اجتماعی: نظریهی بازی
در کدام سوی جاده باید رانندگی کرد؟ اگر در ژاپن، بریتانیا، یا اندونزی زندگی کنید، باید سمت چپ جاده برانید. اگر ساکن کرهی جنوبی، فرانسه، یا ایالات متحده باشید، بایستی سمت راست جاده رانندگی کنید. اگر در سوئد بزرگ شده باشید، آنوقت تا ۵ بعدازظهر روز سوم سپتامبر ۱۹۶۷ در سمت چپ، و در ساعت ۵.۰۱ دقیقه بعد ازظهر شروع به راندن در سمت راست جاده کردهاید. دولت قانونی گذارده است، و ما از آن تبعیت میکنیم.
اما بیایید فرض کنید که ما حق انتخاب را به خود رانندگان دادهایم تا نفع شخصی خود را پی بگیرند و بتوانند هر سمت جاده را انتخاب کنند. اگر هرکس دیگری دارد در راست جاده میراند، چیزی به نام منفعت شخصی کافی است تا رانندهای را تحریک به راندن در همان سمت جاده کند. توجه به دیگر رانندگان، یا تمایل به پیروی از قانون، در چنین وضعیتی ضرورتی نخواهد داشت.
سیاستگذاری برای ارتقای رفاه مردم مستلزم فهم تفاوت میان دو گونه وضعیت است: 1- وضعیتهایی که در آنها منفعت شخصی میتواند رفاه عمومی را ارتقا دهد، و 2- وضعیتهایی که منفعت شخصی در آنها به نتایج نامطلوب ختم میگردد. برای تحلیل این امر نظریهی بازی را معرفی خواهیم کرد که شیوهای است برای مدلسازی سازوکارهای تعامل مردم.
در فصل سوم دیدیم که یک دانشجو برای تصمیمگیری درمورد میزان مطالعه و یک کشاورز برای تصمیمگیری دربارهی میزان سختی کار، هردو با یکسری گزینههای شدنی مواجه شدند، که یک کارکرد تولید آنها را تعیین کرده بود. این شخص سپس برای حصول به بهترین خروجی ممکن تصمیماتی میگیرد. اما در مدلهایی که تا بدینجا مطالعه کردهایم، نتیجه به کردههای افراد بستگی ندارد. نه دانشجو و نه کشاورز درگیر یک تعامل اجتماعی نبودهاند.
تعاملات اجتماعی و استراتژیک
- تعامل استراتژیک
- تعاملی اجتماعی است که در آن مشارکتکنندگان آگاهاند که چگونه کنشهایشان چگونه بر دیگران تأثیر میگذارد (و چگونه کنشهای دیگران بر آنها تأثیر میگذارد).
- بازی
- نوعی الگوی تعامل راهبردی است که توصیفی از بازیگران، استراتژیهای مقرون به صرفه، اطلاعاتی که در اختیار بازیگران است، و پاداشهای آنها را بدست میدهد. همچنین نگاه کنید به: نظریه بازی.
در فصل حاضر کنشهای متقابل اجتماعی را بررسی میکنیم، به معنای وضعیتهایی که در آن تعداد دو یا چند نفر دخیلاند، و کنشهای هریک از افراد هم خروجی خود آنها و هم خروجیهای افراد دیگر را تحت تاثیر قرار میدهد. برای مثال، انتخاب یک شخص دربارهی میزان گرم کردن خانهاش بر تجربهی هرکسی از تغییرات جهانی آب و هوا تاثیر میکند.
در اینجا از چهار اصطلاح استفاده میکنیم:
- استراتژی
- نوعی از کنش (یا سلسلهای از کنشها) که فرد وقتی نسبت به وابستگیِ دوجانبه نتایج برای خود و دیگران آگاهی دارد، ممکن است در پیش بگیرد. نتایج نه تنها به کنشهای آن فرد، بلکه به کنشهای دیگران هم بستگی دارند.
- زمانی که مردم درگیر یک تعامل اجتماعی بوده و به راههای تاثیر کنشهایشان بر دیگران آگاه باشند، و بالعکس، ما آنرا یک تعامل استراتژیک میخوانیم.
- استراتژی عبارت است از کنش یا سلسله کنشهای احتمالی شخص در عین وقوف به این واقعیت که نتایج کار برای او و برای دیگران متقابلاً به هم وابستهاند. خروجیها نه تنها به کنشهای آن شخص، بلکه همچنین به کنشهای دیگران بستگی دارد.
- مدلهای تعامل استراتژیک تحت عنوان بازی تشریح میشوند.
- نظریهی بازی عبارت است از یکسری مدلهای تعامل استراتژیک. وسیعا در اقتصاد و جاهای دیگر در علوم اجتماعی کاربرد دارد.
برای اینکه ببینیم نظریهی بازی چگونه میتواند کنشهای متقابل استراتژیک را روشن کند، دو کشاورز را با نامهای آنیل و بالا تصور کنید که به مشکلی برخوردهاند: کاساوا بکارند یا برنج؟ فرض میکنیم که آنها توان کاشت هر دو نوع محصول را دارند، اما در یک نوبت تنها میتوانند یک نوع را بکارند.
- تقسیم کار
- تخصصیشدنِ تولیدکنندهها برای انجام وظایفِ مختلف در فرآیند تولید. همچنین تحت عنوان تخصصیشدن هم شناخته میشود.
زمین آنیل بیشتر مناسب رشد کاساوا است، حال آنکه زمین بالا مناسب رشد برنج است. دو کشاورز ناگزیرند نوعی تقسیم کار، ایجاد کنند، به این معنا که، کدام زمین را به چه محصولی اختصاص دهند. آنها مستقلا و پیش خود این تصمیم را میگیرند، یعنی لزوماً با هم ملاقات نمیکنند تا درباره مجموعه اقداماتشان با هم بحث کنند.
( فرض استقلال ممکن است در الگویی متشکل از دو نفر کمی غریب بنظرآید، اما بعدها منطق مشابهی را در رابطه با وضعیتهایی مثل تغییرات اقلیمی بکار میگیریم، که در آن صدها و بلکه میلیونها تن از مردمی تعامل دارند که اغلب با هم کاملا غریبهاند. لذا این فرض که آنیل و بالا قبل از انجام کنش به توافق مشترکی نمیرسند، برای ما مفید است.)
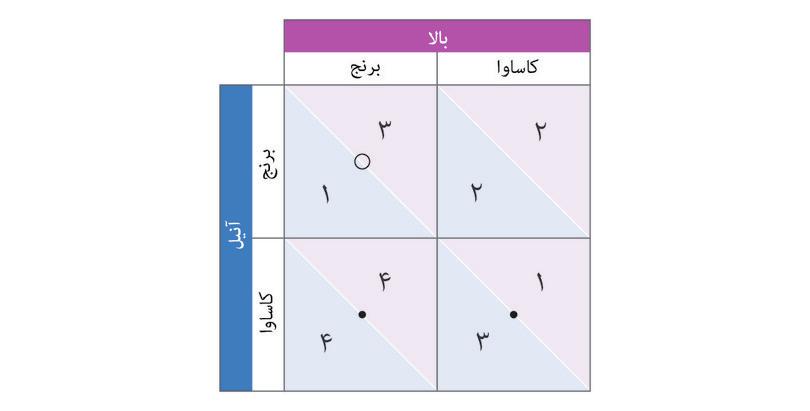
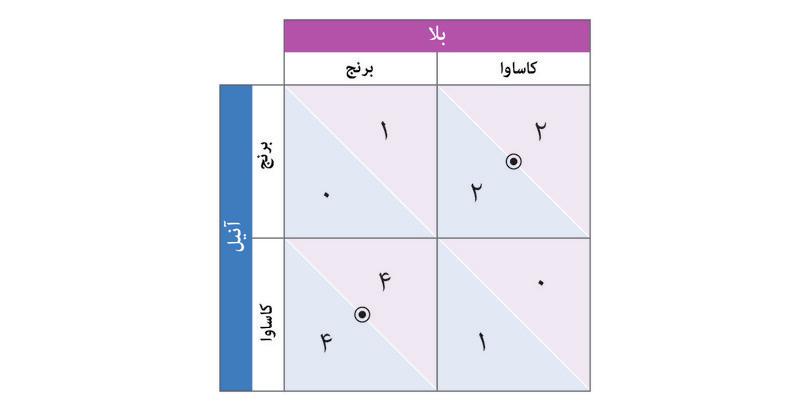
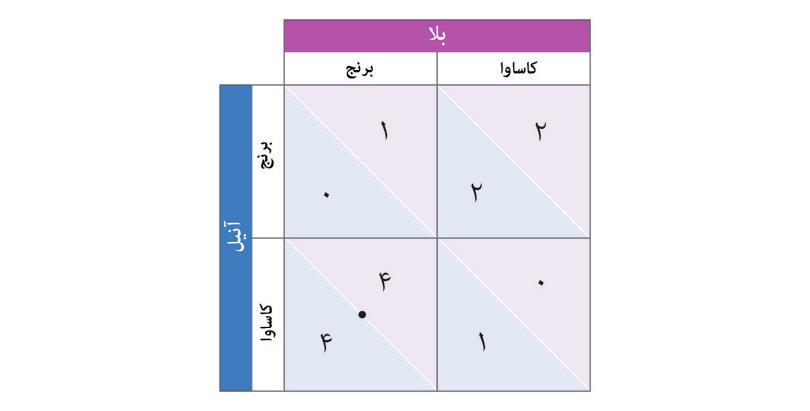
هردوی آنها هرگونه محصول تولیدی خود را در بازار ده کناری میفروشند. در روز برپایی بازار، اگر برنج کمتری به بازار ببرند، قیمت برنج بالاتر خواهد رفت. همین نکته دربارهی کاساوا هم صدق میکند. شکل ۴.۱ تعامل آنها را توصیف میکند، که همانچیزی است که ما آنرا یک بازی میگوییم. بگذارید توضیح دهیم که شکل ۴.۱ چه معنایی میدهد، چرا که در ادامه هم به کرات با آن مواجه خواهید شد.
بازی
توصیفی از یک تعامل اجتماعی که مشخصههای زیر را در برمیگیرد:
- بازیکنان: چه کسی با چه کسی در تعامل است؟
- استراتژیهای مقرون بهصرفه: کدام کنشها را بازیگران میتوانند انجام دهند؟
- اطلاعات: آنچه هر بازیگری در هنگام تصمیمگیری از آن خبر دارد؟
- پاداشها: خروجیهای ممکن برای هریک از بازیگران از ترکیبهای احتمالی کنشها کدامند؟
ردیفهای جدول گزینههای آنیل هستند؛ ستونها هم گزینههای بالا. آنیل را «بازیکن ردیفی» و بالا را «بازیکن ستونی» مینامیم.
وقتی یک تعامل در جدولی مثل شکل ۴.۱، ارائه شود، هر مدخلی در آن نمایانگر خروجی یک وضعیت فرضی است. برای مثال، خانهی چپ بالا را باید اینگونه تفسیر کرد:
«فرض کنید(به هر دلیلی) که آنیل و بالا هردو برنج کاشتهاند. [در اینصورت]چه پیش خواهد آمد؟».
چهار وضعیت فرضی ممکن وجود دارد. نشان میدهد که در هر موردی چه رخ خواهد داد. شکل ۴.۱.
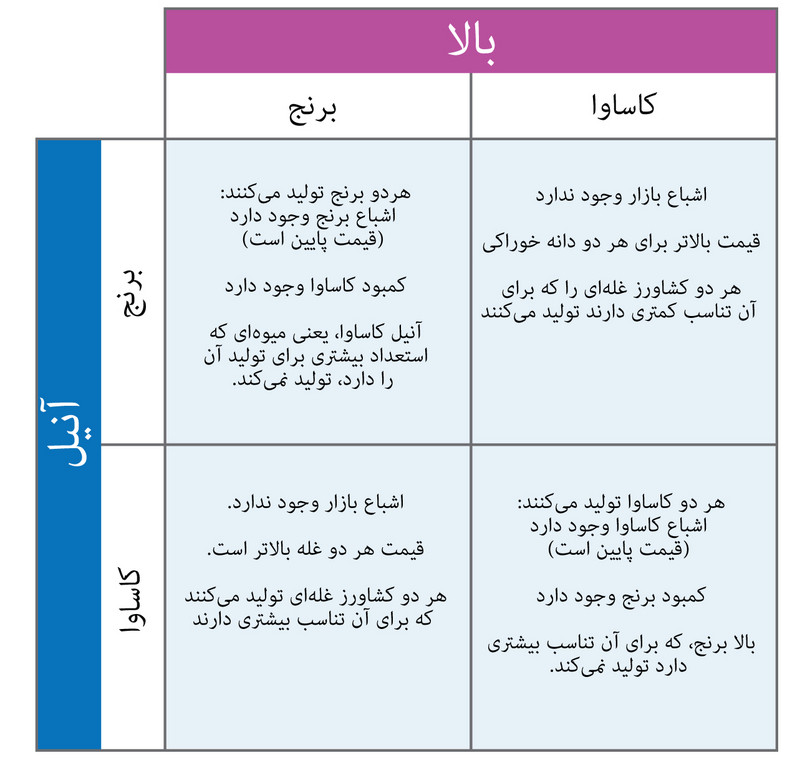
کنشهای متقابل اجتماعی در بازی دست نامرئی.
شکل ۴.۱ کنشهای متقابل اجتماعی در بازی دست نامرئی.
برای سادهسازی مدل چنین فرض میکنیم که:
- هیچ شخص دیگری [غیر از ایندو] وارد این تعامل نمیشود و یا به هرنحوی تحت تاثیر کنشها قرار نمیگیرد.
- تنها تصمیمی که آنیل و بالا بایستی اتخاذ کنند انتخاب نوع محصول برای کشت است.
- آنیل و بالا فقط یکبار باهم تعامل دارند( این وضعیت را بازی یکنوبته میگویند).
- آنها همزمان با هم تصمیم میگیرند: در لحظهی تصمیمگیری از تصمیم دیگری خبر ندارند.
- پاداشها
- سودی که از قبلِ کنشهای مشترک همه بازیگران، عاید هر بازیکن میشود.
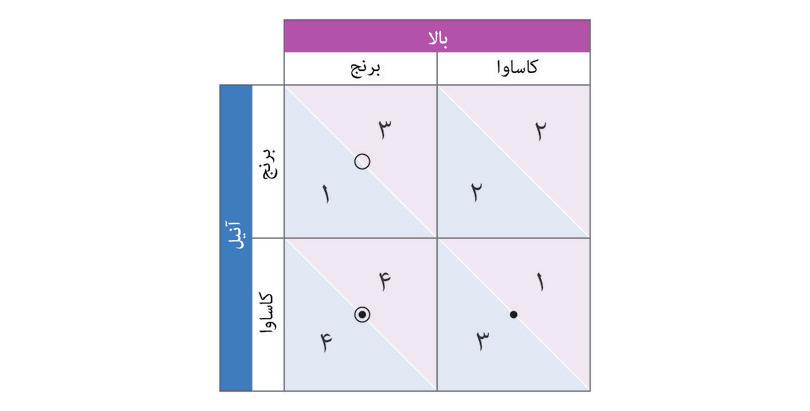
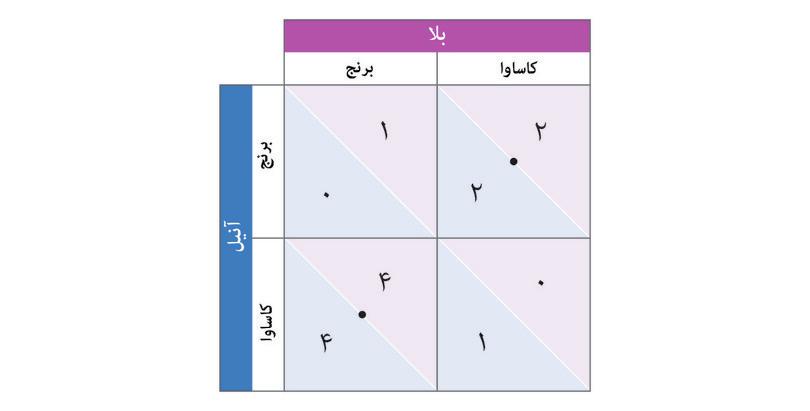
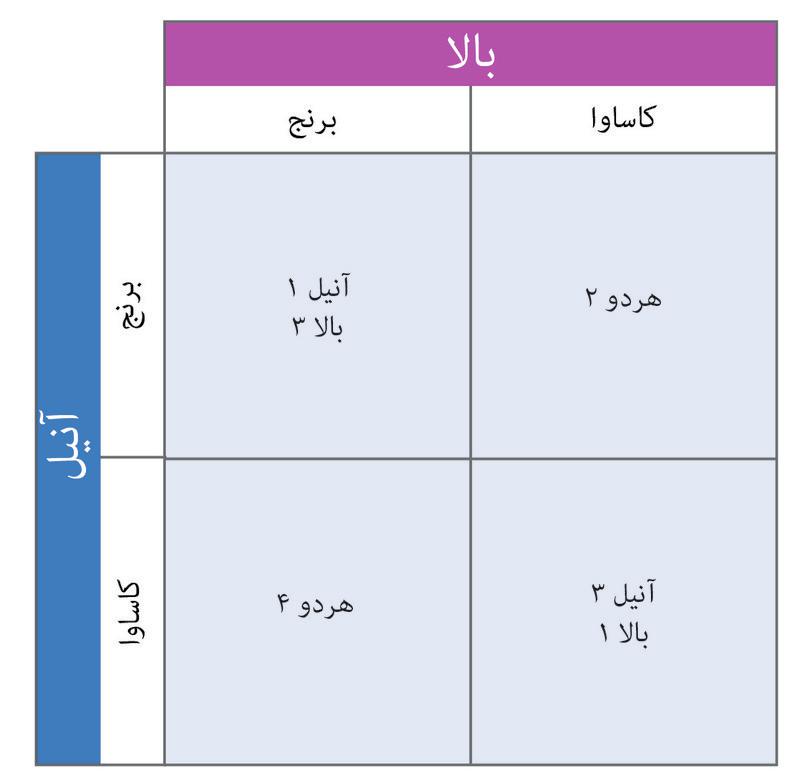
شکل ۴.۲الف پاداشها میزان پاداش برای آنیل و بالا را در هریک از چهار وضعیت فرضی نشان میدهدـ منظور نتیجهای است که در صورت اتخاذ کنشهای ردیفی و ستونی فرضی، نصیب آنها خواهد شد. ازآنجایی که درآمدشان به قیمتهای بازار بستگی دارد، و این یکی بهنوبهی خود به تصمیمات آندو بسته است، لذا ما این وضعیت را نوعی بازی «دست نامرئی» نامیدهایم.
بازدهی در بازی دست نامرئی
شکل ۴.۲الف بازدهی در بازی دست نامرئی
- قیمت بازار وقتی از یک محصول لبریز شود پایین میآید، بههمین دلیل هم اگر هریک زمینشان را به کشت یک محصول اختصاص میدادند، نتیجهی بهتری میگرفتند تا اینکه هر دو یک محصول [مشابه] تولید کنند.
- وقتی که کالاهای مختلفی تولید کنند باز اگر هر شخصی زمینش را به کشت محصول مناسب با آن اختصاص دهد عایدی بهتری خواهند داشت.
پرسش ۴.۱ (این سئوال را پاسخ گویید)
در یک بازیِ یک نوبته همزمان:
- بازیِ همزمان( در برابرِ بازیِ ترتیبی sequential game) بدان معناست که همهیِ بازیکنانِ دخیل بطور همزمان تصمیم خود را دربارهیِ کنشِ خود میگیرند.
- در بازیِ یکنوبته (در برابرِ بازیِ مکرر) هیچ آیندهای در کار نیست: کنشها تنها یکبار واقع میشوند.
- تصمیمی که بازیکنان میگیرند، به دور از همکاری و با انگیزهیِ منفعتِ شخصی است.
- یک عنصرِ اساسی در بازیهایِ استراتژیک این است که در صورتِ مشخص بودنِ انتخابهایِ موجود، هر بازیکنی کنشهایِ احتمالیِ بازیکنانِ دیگر را درنظرمیگیرد.
۴.۲ تعادل در بازی دست نامرئی
- بهترین پاسخ
- در نظریه بازی، استراتژیای است که بالاترین پاداش را با توجه به استراتژیهای برگزیده سایر بازیگران به بازیگر اختصاص میدهد.
نظریهی بازی توصیفگر کنشهای متقابل اجتماعی است، اما همچنین میتواند در مورد اتفاقات آتی پیشبینیهایی ارائه دهد. برای پیشبینی خروجی یک بازی به مفهوم دیگری نیازمندیم: بهترین پاسخ. و آن نوعی استراتژی است که، به فرض درنظرگیری استراتژیهایی که بازیکنان دیگر اتخاذ کردهاند، بالاترین بازدهی را برای بازیکن در پی دارد.
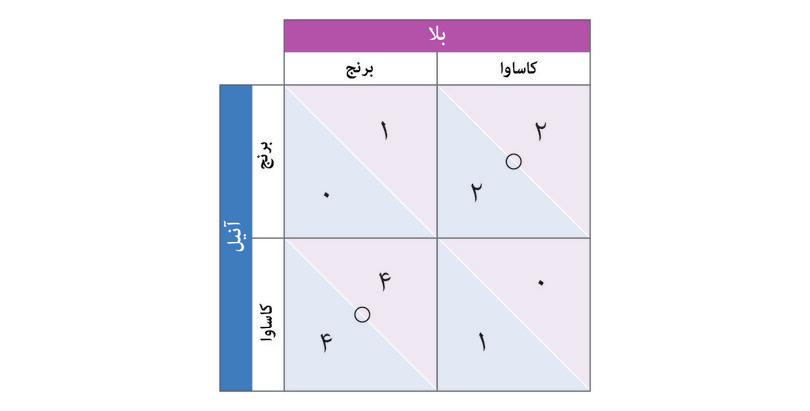
در شکل ۴.۲ب میزان بازدهی برای آنیل و بالادر بازی دست نامرئی را آوردهایم که با استفاده از یک واحد استاندارد به نام ماتریس پاداش بدست آمده است. بسادگی هرگونه آرایش عددی راست گوشه (در اینمورد مربعی) را ماتریس میگوییم. عدد اول در هر خانه نمایانگر پاداش حاصله برای بازیکن ردیفی است( که نامش با A شروع میشود تا فراموش نکنیم که بازدهی اول با اوست). عدد دوم نیز بازدهی بازیکن ستونی ما را نشان میدهد.
به بهترین پاسخها در این بازی فکر کنید. فرض کنید که آنیل خود شما هستید، و شما وضع فرضیای را متصور میشوید که بالا در آن تصمیم به بارآوردن برنج گرفته است. کدام پاسخ بالاترین بازدهی را برای شما بهدنبال دارد؟ اگر کاساوا بکارید چه؟ (در اینصورت شماـ که آنیل باشیدـ به بازدهی ۴ میرسید، اما اگر درعوض فقط برنج بکارید فقط به بازدهی ۱ خواهید رسید).
- استراتژی مسلط
- کنشی که صرفنظر از کنش سایر بازیکنان، بالاترین پاداش را به یک بازیکن اختصاص میدهد.
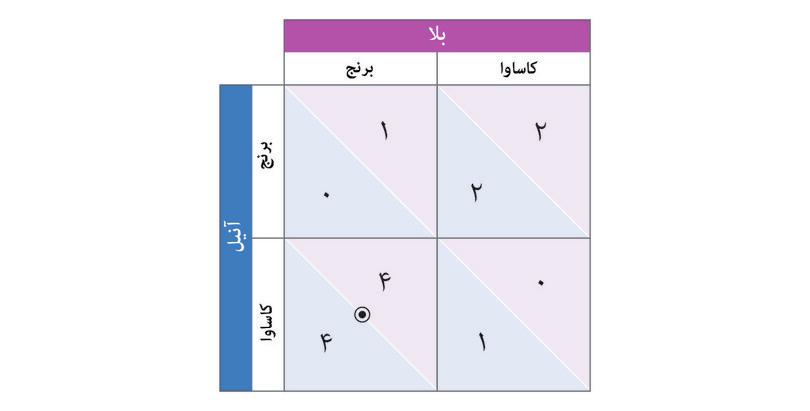
با استفاده از مراحل نشان داده شده درشکل ۴.۲ب ببینید که چگونه کاشت کاساوا هم میتواند بهترین پاسخ آنیل باشد، اگر که بالا کاساوا بکارد. پس کاشتن کاساوا استراتژی مسلط: آنیل است: بالاترین میزان بازدهی را برایش به همراه دارد، حالا بالا هر چیزی که میخواهد بکارد. خواهید دید که بالا نیز در این بازی یک استراتژی مسلط دارد. خطوط کناری جدول همچنین روشی دستی و آسان برای ردگیری بهترین پاسخها در اختیار شما مینهد: با جا دادن نقطهها و دایرهها در ماترسیِ بازدهی.
بخاطر برخورداری هردو بازیکن از یک استراتژی مسلط، میتوانیم یک پیشبینی ساده دربارهی کنشهای آنها داشته باشیم: اینکه استراتژی مسلط خود را به بازی وارد میکنند. آنیل کاساوا خواهد کاشت، و بالا برنجکاری میکند.
- توازن استراتژی مسلط
- نوعی نتیجه بازی که در آن هر بازیگر استراتژی مسلط خود را بازی میکند.
این جفت استراتژی مذکور بهعبارتی توازن استراتژی مسلط بازی اند.
بخاطر دارید که در فصل ۲ توازن را بهعنوان یک وضعیت خود-تداوم-بخش تعریف کردیم: در سود تغییری ایجاد نمیشود. دراین مورد، آنیل که کاساوا و بالا که برنج میکارند، نوعی توازن ایجاد شده است، چراکه هیچیک از آنها قبل از اطلاع از انتخاب بازیکن دیگر، نمیخواهد تصمیم خود را عوض کند.
اگر متوجه شویم که هر دو بازیکن درگیر در یک بازی دونفره استراتژی مسلطی دارند، آنوقت میگوییم که بازی برخوردار از یک توازن استراتژی مسلط است. چنانکه بعدا میبینیم، چنین اتفاقی همیشه رخ نمیدهد. اما وقتی رخ داد، میتوانیم پیشبینی کنیم که استراتژیهایی که وارد بازی میشوند همینها خواهند بود.
انتخاب نوع محصول ازجانب آنیل و بالا از تصمیم شخص دیگر تاثیر نمیپذیرد، زیراکه آندو برخوردار از یک استراتژی مسلط هستند. و این مشابه مدلهایی است که در فصل ۳ دیدیم، که در آنها میزان ساعات انتخابی الکسی برای مطالعه، یا ساعات کاری آنجلا، به کنشهای دیگران بستگی نداشت. دراینجا اما، ولواینکه تصمیمگیری به اقدامات دیگران بستگی نداشته باشد، بازدهی اما[به کنشهای دیگران] بستگی دارد. مثلا اگر آنیل استراتژی مسلط خود(کاساوا) را بازی میکند، بهتر است دست از کار بکشد، اگر که بالا برنج را بازی کند، اما اگر بالا هم کاساوا بکارد، استراتژی مسلط او کارگر خواهد افتاد.
در توازن استراتژی مسلط، آنیل و بالا بهشکل ویژه به تولید آن محصولی پرداختهاند که زمینشان بیشتر قابلیت آن را دارد. بهعبارتی ساده، پیگیری منفعت شخصی ـ انتخاب آن استراتژی که بالاترین بازدهی را برایشان به ارمغان آوردـ به خروجیای منتهی شده است که:
- بهترین خروجی از میان چهار خروجی ممکن برای هر بازیکن بوده است
- استراتژیای بوده است که درصورت همکاری دو کشاورز بزرگترین بازدهی کل را برای آنها آورده است.
در این مثال، توازن استراتژی مسلط همان خروجیای است که نصیب هریک از آنان میشد، اگر که راهی برای هماهنگسازی تصمیمات خود داشتند. هرچندکه آنها مستقلانه منفعت شخصی خود را پیگرفتهاند، اما بهنوعی،«چنانکه گویی توسط دستی نامرئی»، به یک خروجی سوق داده میشوند که برای هر دو بهترین خروجی بود.
مسائل اقتصادی واقعی هرگز به این سادگی نیستند، اما منطق بنیانی یکسانی دارند. گاهی تعقیب منفعت شخصی بدون درنظرگیری دیگران بلحاظ اخلاقی بد ارزیابی شده است، لیکن با مطالعهی اقتصاد به مواردی برمیخوریم که [این تعقیب منفعت شخصی] در آنها به خروجیهای مطلوب اجتماعی میانجامد. مواردی هم هستند، البته، که تعقیب منفعت شخصی در آنها منجر به نتایجی میشود که برای هیچیک از بازیکنان نفع شخصی محسوب نمیشود. بازی تنگنای زندانی، که بعدازین بررسی خواهیم کرد، یکی از این وضعیتها را توصیف میکند.
پرسش ۴.۲ ( یکی از پاسخها را برگزینید)
برایان رفتن به سینما را بیشتر از تماشایِ فوتبال دوست دارد. ازسویِ دیگر، آنا تماشایِ فوتبال را بر سینما رفتن ترجیح میدهد. در هر دو صورت، هردویِ آنها باهم بودن را بر سپری کردنِ جداگانهیِ بعدازظهر ترجیح میدهند. جدولِ زیر سطوحِ شادی (بازدهی) آنا و برایان را، بسته به نوعِ فعالیتِ انتخابیِ آنها، ارائه میدهد(عدد اول سطحِ شادیِ برایان و عدد دوم ازآنِ آنا است)
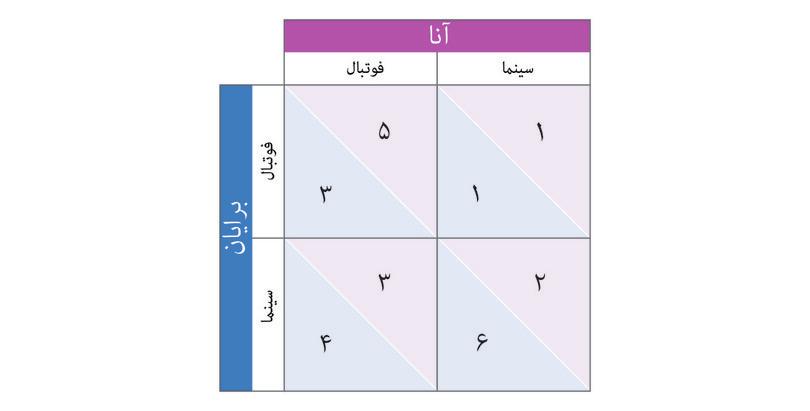
براساسِ اطلاعاتِ فوقالذکر میتوانیم نتیجه بگیریم که:
- استراتژیِ مسلط برایِ برایان آنست که به سینما برود.
- توازنِ استراتژیِ مسلط، خروجیای است که در آن هر بازیکنی استراتژیِ مسلطِ خود را بازی میکند. در این بازی توازن برمیگردد به سینما / فوتبال، با بازدهیِ ۴ / ۳.
- اگر آندو باهم به سینما بروند، آنا به بالاترین سطح شادی نایل میآید. و به همان ترتیب، بالاترین سطح شادی برایان وقتی است که هردو با هم فوتبال ببینند.
- (سینما/فوتبال)یک توازنِ استراتژیِ مسلط است. فقدانِ هرگونه انگیزه برایِ انحراف از این توازن یکی از خصایصِ هرگونه توازنِ استراتژیکِ مسلطی است.
وقتی توافقی میان اقتصاددانان وجود ندارد انسان اقتصادی در بوتهی بحث: آیا مردم تماما خودخواهاند؟
قرنها اقتصاددانان و تقریبا همه این موضوع را به بحث گرفتهاند که آیا مردم بیکموکاست درپی منفعت شخصیاند یا نه، گاهی از کمک به دیگران خوشحال میشوند، حتی اگر اینکار برایشان هزینه داشته باشد؟ انسان اقتصادی لقبی است که به آدم خودخواه و شخصیت محاسبهگری دادهاند که در کتابهای رشتهی اقتصاد میبینید. آیا اقتصاددانان در به تصویر کشیدن انسان اقتصادی درمقام تنها بازیگر صحنهی اقتصاد، محق بودهاند؟
آدام اسمیت نیز در کتاب مشابهی که اول بار درآن از عبارت «دست نامرئی» استفاده کرد، روشن کرده است که به نظر او ما انسان اقتصادی نیستیم: «هرچقدر هم که بشر را خودخواه فرض کنیم، بوضوح در طبیعت او اصولی وجود دارد که او را به بخت دیگران علاقمند میکند، و خوشبختی آنها را برای خود ضروری میگیرد، هرچند چیزی عاید او نکند، جز لذت دیدن آن».( آدام اسمیت، نظریهی عواطف اخلاقی، ۱۷۵۹). * اما اغلب اقتصاددانان بعد از اسمیت با این نظر مخالفت کردهاند. فرانسیس اِجوُرث، بنیانگذار اقتصاد مدرن، در سال ۱۸۸۱ در کتاب خود *فیزیک ریاضیات بهروشنی تمام چنین موضعی دارد: «اصل اول اقتصاد اینست که هر عاملی فقط با منفعت شخصی به کار میافتد.» 6
با تمام این تفاسیر اما هرکسی، اگر خود نکرده باشد، لااقل دیده که برخی در وضعیتهایی که شانس کمی برای پاداش وجود دارد، کارهای مهربانانه و شجاعانهای به نیابت از دیگران انجام دادهاند. پرسش مطرح برای اقتصاددانان اینست: آیا باید عدم خودخواهی روشنی که در این کنشها هست را بخشی از چگونگی خردورزی دربارهی رفتار دانست؟
برخی میگویند«خیر»: بهتر است که بسیاری از کنشهای بهظاهر سخاوتمندانه را بهمثابهی تلاشهایی برای حصول به وجههای مطلوب فهم کرد که در آینده به کنشگر سود خواهد رسانید.
شاید کمک به دیگران و مشاهدهی هنجارهای اجتماعی فقط در افقی بلندمدت است که منفعت شخصی محسوب میشوند. اچ.ال.منکن مقالهنویس چنین میاندیشد: « وجدان، آن ندای درونی است که به شما هشدار میدهد که شاید کسی دارد شما را دید میزند».7
پس از دههی ۱۹۹۰ در تلاشی برای حل و فصل مناقشات مربوط به زمینههای تجربی، اقتصاددانان در سرتاسر جهان صدها آزمایش ترتیب دادهاند که در آنها میتوان رفتار افراد (دانشآموزان، کشاورزان، صیادان وال، کارگران انبار) را درهنگام اتخاذ تصمیمات واقعی دربارهی تسهیم و با بکارگیری بازیهای اقتصادی، تحت مشاهده گرفت.
- دوجانبه بودن
- ترجیح مهربانی و یاریگری در برابر افراد مهربان و یاریگر، و محروم کردن افراد فاقد مهربانی و یاریگری از مهربانی خود.
- دیگرخواهی
- تمایل به متحمل شدن هزینه درقبالِ منتفع شدن فردی دیگر
تقریبا همیشه در این آزمایشها میزانی از رفتار معطوف به منفعت شخصی دیده میشود. اما دیگرخواهی، دوجانبه بودن، نفرت از نابرابری، و دیگر ترجیحاتی که با منفعت شخصی توفیر دارند، مشاهده میشود. انسان اقتصادی در بسیاری از این آزمایشها در اقلیت است. و این نکته صادق است، حتی وقتی که مبالغ قسمتشده(یا مانده برای خود شخص)، بالغ بر دستمزد چندین روز کاری او باشد.
آیا مناقشه برطرف شده است؟ بسیاری از اقتصاددانان اینگونه میاندیشند و حالا علاوه بر انسان اقتصادی، مردمی گاه دیگرخواه، گاه مخالف نابرابری، و گاه همـنفعخواهانه را هم لحاظ میکنند. آنها خاطرنشان میکنند که فرض منفعت شخصی برای بسیاری از موقعیتهای اقتصادی فرض درستی است، همچون در خرید کردن یا وقتی بنگاههای اقتصادی از تکنولوژی برای به حداکثر رساندن سود خود استفاده میکنند. اما در موقعیتهای دیگری مثل چگونگی پرداخت مالیات، یا چرایی کار سخت برای کارفرما، فرض چندان درستی نیست.
۴.۳ تنگنای زندانیان
تصور کنید که آنیل و بالا اکنون با مسالهی متفاوتی مواجهاند. هریک در حال تصمیمگیری هستند که چگونه به مقابله با آفاتی که محصولات آنها در زمینهای همجوار را نابود میکند بپردازند. هرکدام دو استراتژی مقرون بهصرفه دارند:
- اولی اینکه از یک کود شیمیایی ارزانقیمت به نام ترمیناتور استفاده کنند. این ماده تا شعاع چند مایلی هر حشرهای را نابود میکند. ترمیناتور همچنین به مخزن آب مشترک آنها نیز رخنه میکند.
- دومی اینکه بهجای یک مادهی شیمیایی از کنترل آفَت ترکیبی ( IPC) استفاده کنند. کشاورزی که از این شیوه استفاده میکند، حشرات سودمندی را به زمین وارد میکند. حشرات سودمند حشرات آفَت را میخورند.
اگر فقط یکی از آنها ترمیناتور را انتخاب کند، زیان وارده کاملا محدود خواهدبود. اگر هردوی آنها ترمیناتور را برگزینند، آلودگی آب به مسالهای جدی بدل میشود، و آنوقت میبایست یک سیستم تصفیهی گرانقیمت بخرند. شکل ۴.۳الف و ۴.۳ب تعامل آنها را توصیف میکند.
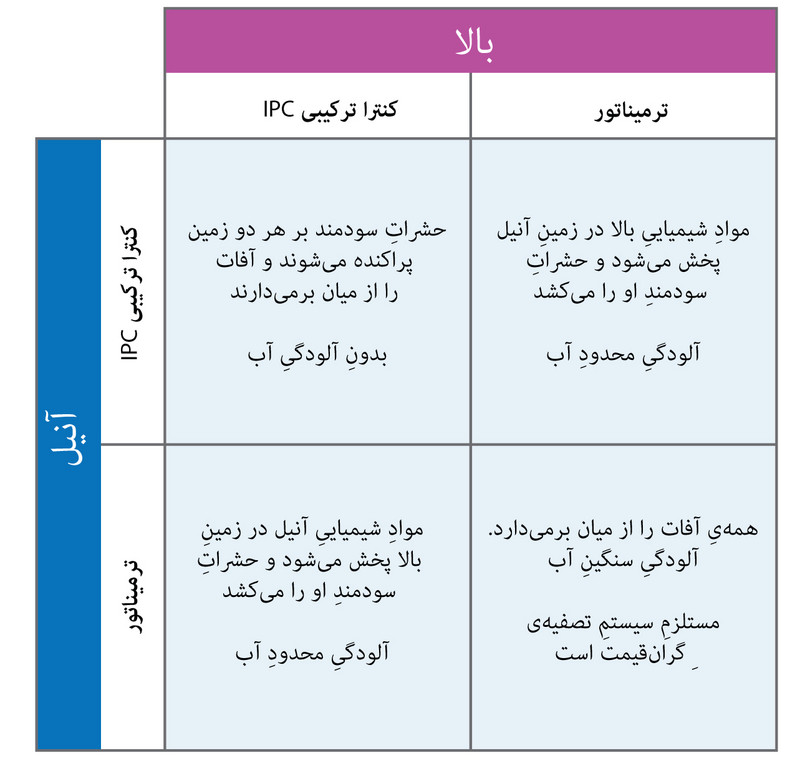
کنشهای متقابل اجتماعی در بازی کنترل آفَت.
شکل ۴.۳الف کنشهای متقابل اجتماعی در بازی کنترل آفَت.
هم آنیل و هم بالا از این خروجیها آگاهند. بهعنوان یک نتیجه آنها میدانند که بازدهی آنها( مقدار پولی که در فصل برداشت درمیآورند، منهای هزینههای مربوط به استراتژی کنترل آفَت و نصب فیلتراسیون آب در صورت لزوم)نه تنها به انتخاب تک تک آنها، که به انتخاب شخص دیگر هم بستگی دارد. این نمونهای از یک تعامل استراتژیک است.
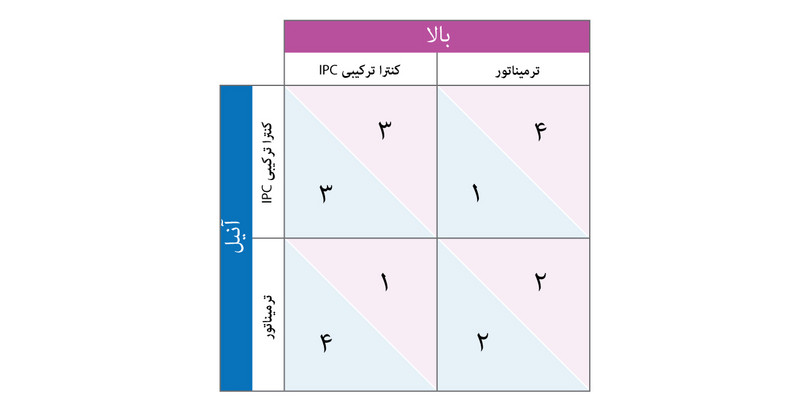
ماتریس بازدهی برای بازی کنترل آفَت
شکل ۴.۳ب ماتریس بازدهی برای بازی کنترل آفَت
آنها چگونه بازی را پیش خواهند برد؟ برای پاسخ میتوانیم از همان روش بکارگرفته در بخش پیش را استفاده کنیم(برای خودتان نقطه و دایرهها را در ماتریس بازدهی جای دهید)
بهترین پاسخهای آنیل:
- درصورت استفادهی بالا از IPC: ترمیناتور (امحای ارزان آفات با آلودگی ناچیز آب).
- در صورت استفادهی بالا از ترمیناتور: ترمیناتور (IPC هزینه بردارتر است و جواب نمیدهد، چراکه مواد شیمیایی بالا حشرات سودمند را خواهد کشت).
لذا ترمیناتور، استراتژی مسلط آنیل است.
بههمین ترتیب، میتوانید دریابید که ترمیناتور استراتژی مسلط بالا نیز هست.
ازآنجایی که ترمیناتور استراتژی مسلط هردوی آنهاست، پیشبینی میکنیم که هر دو آن را بکار گیرند. استفادهی هر دوی بازیکنان از حشرهکش، توازن استراتژی مسلط بازی است.
- تنگنای زندانی
- بازیای که در آن پاداشهای موجود در توازن استراتژی مسلط، برای هر بازیگر، و همچنین در کل، نسبت به وضعیتی که هیچ بازیگری استراتژی مسلط را بازی نکند، پائینتر است.
آنیل و بالا هرکدام بازدهی ۲ را دریافت میکنند. اما اگر بهجای ترمیناتور، IPC را بکار میگرفتند هر دو آسایش بیشتری داشتند. بنابراین نتیجه پیشبینی شده، بهترین نتیجه مقرون بهصرفه نیست. بازی کنترل آفَت نمونه ای از یک بازی موسوم به بازی تنگنای زندانی است.
تنگنای زندانی
نام این بازی برگرفته از حکایتی دربارهی دو زندانی است (آنها را تلما و لوییز مینامیم)، که استراتژی هردو یا متهم کردن (و دست داشتن) دیگری در جرمی است که ممکن است باهم مرتکب شده باشند، و یا تکذیب شراکت دیگری در آن جرم است.
اگر هردو آن را تکذیب کنند، بعد از چندروز بازجویی آزاد میشوند.
اگر یکی از آندو دیگری را متهم کند، و دیگری تکذیب کند، شاکی فیالفور آزاد خواهد شد (محکومیتی درکار نیست)، و در عین حال شخص دیگر به ۱۰ سال زندان محکوم خواهد شد.
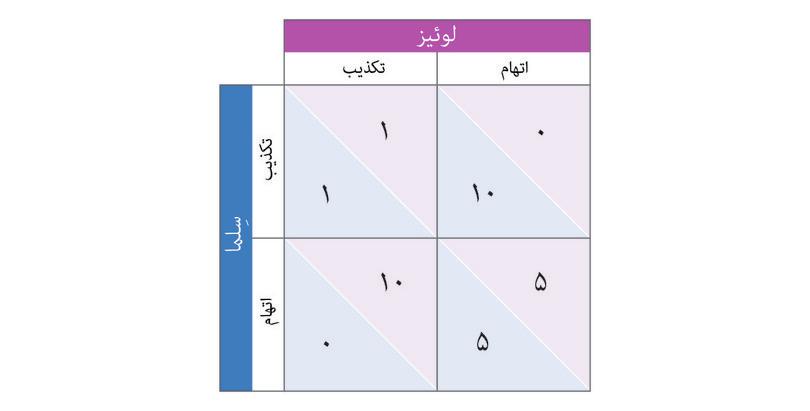
درنهایت، اگر هم تلما و هم لوییز اتهام زدن را انتخاب کنند (بدین معنا که هریک دیگری را به دست داشتن در جرم متهم کند)، در آنصورت هر دو به حبس محکوم میشوند. این حکم بخاطر همکاری آنها با پلیس از ۱۰ به ۵ سال تقلیل یافتهاست. بازدهیهای موجود در بازی در شکل ۴.۴ نشاندادهشدهاند.
![تنگنای زندانی (عدد نتیجه نمایانگر تعداد سالهای زندان است)
: تنگنای زندانی (عدد نتیجه نمایانگر تعداد سالهای زندان است).]()
تنگنای زندانی (عدد نتیجه نمایانگر تعداد سالهای زندان است)
شکل ۴.۴ تنگنای زندانی (عدد نتیجه نمایانگر تعداد سالهای زندان است)
بازدهی برحسب سالهای محکومیت به حبس آمدهاندـ بااین تفاسیر لویی و تلما اعداد پایینی را ترجیح خواهند داد).
در تنگنای زندانی، هردو بازیکن یک استراتژی مسلط دارند(اتهام درمثال فوق) که درصورت اتخاذ آن از سوی هر دو، به بدترین خروجی برای هردو منجر میشود، که اگر هردو استراتژی متفاوتی را(تکذیب در مثال فوق) برمیگزیدند، چنین نمیشد.
حکایت ما دربارهی لویی و تلما حکایتی فرضی است، اما این بازی بر مسائل واقعی بسیاری دلالت دارد. مثلا اگر کلیپ تلویزیونی زیر دربارهی مسابقهی اطلاعات عمومی گلدن بالز Golden Ballsرا ببینید، خواهید دید که یک شخص معمولی تنگنای زندانی را چطور استادانه حل میکند.
در مثالهای اقتصادی، برای اشاره به استراتژی سودبخش متقابل (در اینجا تکذیب) از اصطلاح همیاری/تعاون و برای استراتژی مسلط (در اینجا اتهام) از اصطلاح نقص استفاده میکنند. همیاری به این معنا نیست که بازیکنان بهم بپیوندند و درباره آنچه باید بکنند بحث کنند. قوانین بازی همیشه تصمیماتی هستند که هر یک از بازیکنان مستقلا در قبال یک استراتژی اتخاذ میکند.
تفاوت موجود میان بازی دست نامرئی و تنگنای زندانی نشان میدهد که منفعت شخصی ممکن است به خروجیهای مطلوب منجر شود، اما همچنین میتواند به خروجیهایی بیانجامد که [مورد تایید] و دلخواه هیچکسی نیست. چنین مثالهایی از سویی میتواند به ما کمک کند تا فهم دقیقتری از این داشته باشیم که بازارها چگونه قادرند منفعت شخصی را برای ارتقای سازوکارهای اقتصاد مهار کنند، اما همچنین محدودیتهای بازار راهم یادآور میشوند.
سه وجه تعامل بین آنیل و بالا ما را برآن داشت تا در بازی تنگنای زندان خروجی بدفرجامی را برایشان پیشبینی کنیم:
- آنها هیچ ارزشی برای نتیجه شخص دیگر قائل نشدند، و بااینکار هزینههایی که بخاطر کنش او بر دیگری تحمیل شده را به شمار نیاوردند.
- هیچ راهی نبود که آنیل، بالا و یا هر کس دیگری بتواند کشاورز بهکارگیرندهی حشرهکش را مجبور به جبران مالی خسارات وارده کند.
- آنها قادر به رسیدن به توافقی قبلی دربارهی کنشهای یکدیگر نبودند. اگر قادر به چنین کاری بودند، بسادگی میتوانستند بر سر استفاده از IPC باهم توافق کنند یا کاربرد ترمیناتور را ممنوع کنند.
اگر بتوانیم بر یک یا چند تا از این مسائل فایق آییم، خروجی موردنظر و مطلوب هر دوی آنها درمواردی حاصل خواهد شد. بنابراین در باقی این فصل، شیوههای به انجام رساندن چنین کاری را به آزمون خواهیم گذاشت.
پرسش ۴.۳ (همهیِ پاسخهایِ صحیح را انتخاب کنید)
دیمیتریوس و آمیرا درمقامِ کارگزارانِ مبادلاتِ خارجی برایِ یک بانکِ سرمایهگذاریِ بینالمللی کار میکنند. پلیس برایِ همدستیِ مشکوکِ آنها در تبانی و دستکاری در یکسری معاملات موردِ استنطاق قرار میدهد. جدولِ ذیل هزینههایِ مربوط به هر استراتژی را نشان میدهد( برحسبِ طولِ سالهایِ محکومیت به زندانی که برای هریک صادر میشود)، و بسته به اینکه آیا آنها یکدیگر را متهم و یا جرم را تکذیب میکنند تنظیم شده است. عددِ اول میزانِ نتیجه برایِ دیمیتریوس است، حالآنکه عددِ دومی نتیجه آمیراست(اعدادِ منفی دلالت بر خسارت دارند). فرض کنید که بازی یک بازیِ یک نوبته همزمان است.[پرسش: جدول را به شیوهیِ ما ترسیم کنید]
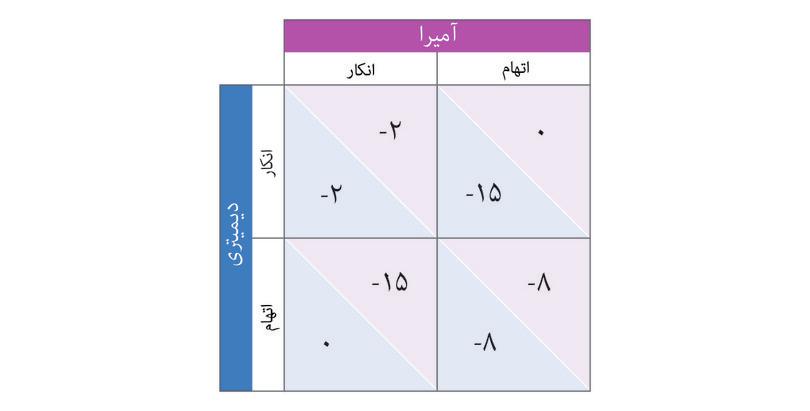
براساسِ این اطلاعات میتوانیم نتیجه بگیریم که:
- تکذیب هم برایِ دیمیتریوس و هم آمیرا یک استراتژیِ مسلط است، پس اتهام خواهند زد.
- اتهامبستن هم برایِ دیمیتریوس هم برایِ آمیرا یک استراتژیِ مسلط است. بنابراین، خروجیای که درآن هردو اتهام میزنند و به حکمِ 8 ساله منتهی میشود، یک توازنِ استراتژیکِ مسلط است.
- صرفنظر از کنشِ دیمیتریوس، اتهامبستن بهترین پاسخِ آمیرا است، پس او همیشه اتهام خواهد زد؛ این یک استراتژیِ مسلط است.
- این خروجی تنها درصورتی حاصل میشود که دیمیتریوس و آمیرا، هردو، تکذیب را پیش بگیرند. تکذیب یک استراتژیِ مسلط برایِ هردویِ آنهاست، پس چنین اتفاقی هرگز نخواهد افتاد.
تمرین ۴.۲ تبلیغات سیاسی
بسیاری از مردم تبلیغات سیاسی( تبلیغات پویشی) را نمونهی کلاسیکی از یک تنگنای زندانی میدانند.
- با مثال زدن از یک کمپین تبلیغاتی اخیر که با آن آشنایی دارید، توضیح دهید که آیا چنین هست یا خیر.
- یک ماتریس نتیجه برای این مورد بنویسید.
۴.۴ ترجیحات و [اولویتهای] اجتماعی: دیگرخواهی
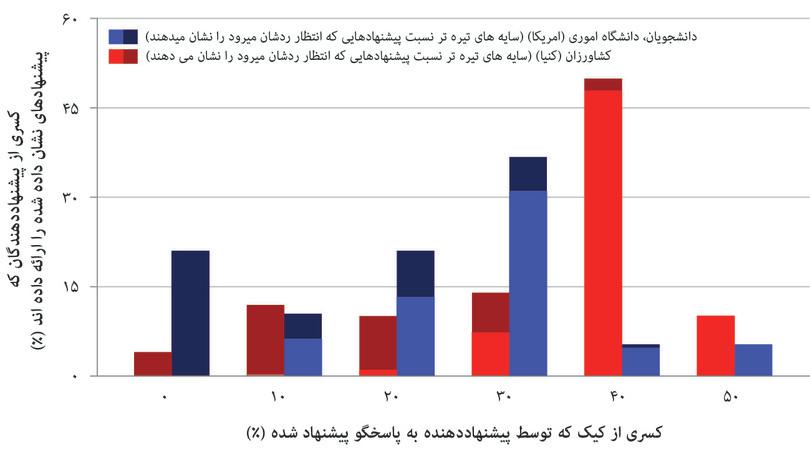
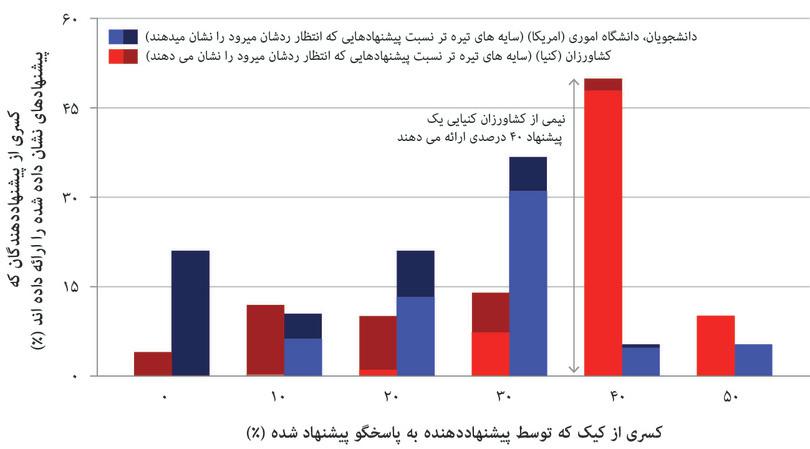
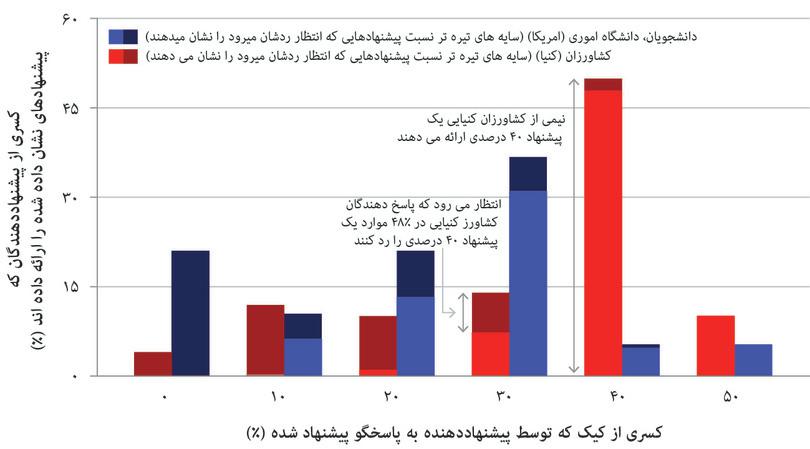
وقتی دانشجویان بازیهای یک نوبته تنگنای زندانی را در کلاس یا در آزمایشهای آزمایشگاهی بازی میکنند ـ گاها برای مبالغ واقعی پول ـ بهطور معمول مشاهده میشود که نیم یا بیش از نیمی از مشارکین استراتژی تعاون و نه نقص را پیش میگیرند، برخلاف وقتی که نقص دوطرفه استراتژی مسلط بازیکنانی باشد که فقط به بازدهی پولی خویش میاندیشند. از تفاسیر این نتایج یکی اینست که بازیکنان دیگرخواه هستند.
برای مثال، اگر آنیل بهحد کفایت به آسیبهایی فکر کند که ممکن است با استفاده از ترمیناتور بر بالا وارد میآید(وقتی که بالاIPC را استفاده میکرد)، درآنصورت بهترین پاسخ آنیل به IPCبالا، IPC میبود. و اگر بالا احساس مشابهی میداشت، درآنصورت IPC بهترین پاسخ متقابلی میبود برای هردوطرف، و دوطرف بیش از این در تنگنای زندانی محبوس نبودند.
اگر ارادهی یک شخص بر تقبل هزینهای به هدف کمک به دیگری باشد، میگوییم آن شخص تمایلات یا ترجیحات دگرخواهانه دارد. در مثال اخیر، آنیل مایل بود از خیر یک واحد نتیجه ۱ بگذرد، چراکه با این کار خسرانی ۲ واحدی بر بالا تحمیل میکرد. هزینهی فرصت انتخاب IPC برای او ۱ بود( وقتی بالا IPC را انتخاب کرده بود)، و یک بهرهی ۲ واحدی هم به توبرهی بالا میریخت، و اینها همه بدین معناستکه او بهنحو دیگرخواهانهای کنش نشان دادهاست.
- ترجیحات اجتماعی
- ترجیحاتی هستند که به نتیجه و تأثیرِ کنش بر دیگران، و همچنین به کنشِ اخلاقی، اهمیت میدهند، حتی اگر اینکار به پاداش پائینتری برای فرد منجر شود.
مدلهای اقتصادیای که در فصل ۳ کار گرفتیم تمایلات اجتماعی را مفروض گرفته بودند: آلکسی دانشجو و آنجلای کشاورز نگران وقت آزاد خود و نمرات یا مصرف شخصی خود بودند. مردم اما معمولا نه تنها نگران سرنوشت خویش، که همچنین نگران سرنوشت دیگران نیز هستند. اینجا میگوییم که فرد مذکور تمایلات اجتماعی دارد. دگرخواهی مثالی از یک ترجیحات اجتماعیاست. بدخواهی و حسادت نیز تمایلات اجتماعی هستند.
تمایلات دیگرخواهانه بهمثابهی منحنیهای بیتفاوتی
در فصول پیش برای مدلسازی از رفتار آنجلا و آلکسی منحنیهای بیتفاوتی و مجموعههای مقرون بهصرفه را بکار گرفتیم. برای مطالعهی چگونگی تعامل مردم، وقتی تمایلات اجتماعی بخشی از انگیزهی آنها باشد، میتوانیم همانکار را انجام دهیم.
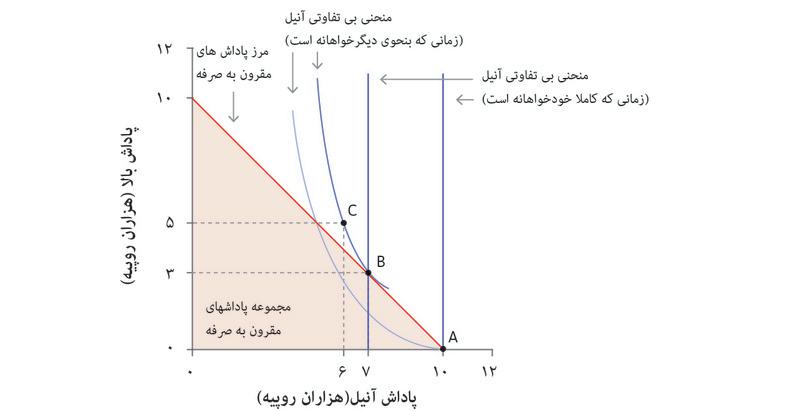
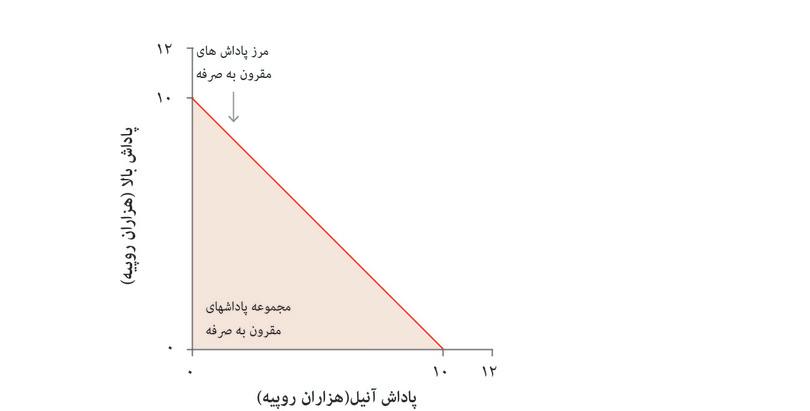
وضعیت زیر را تصور کنید: آنیل چند بلیط بختآزمایی ملی دارد که یکی از آنها جایزهای ۱۰۰۰۰ روپیهای برایش به ارمغان داشته است. البته او میتواند همهی این پول را برای خودش نگهدارد، اما همچنین میتواند بخشی ازآن را بدهد به همسایهاش بالا. شکل ۴.۵ وضعیت را بهشکل گرافیکی ارائه میدهد. محور افقی نمایانگر مبلغ پولی است( به هزار روپیه) که آنیل برای خودش نگه میدارد، و محور عمودی مقدارپولی است که به بالا میدهد. هر نقطه(x،y) مجموع پول آنیل(x) و بالا ( y) است. مثلث هاشور خورده تصمیمات عملی و امکانپذیر آنیل را تصویر میکند. در گوشهی محور افقی(۱۰، ۰)، آنیل همهی پول را نزد خود نگهداشته است. در گوشهی دیگر بر محور عمودی( ۰،۱۰)، آنیل همهی پول را به بالا میسپارد. مجموعهی امکانپذیر آنیل همان منطقهی هاشور خورده است.
- حاصلجمع صفر
- بازیای است که در آن حاصلجمعِ بدستآوردن و ازدستدادنِ پاداش برای افراد، در کلیه ترکیباتِ استراتژیهایی که میتوانند اتخاذ کنند، مجموعاً صفر است.
مرز منطقهی هاشور خورده مرز مقرون بهصرفهگی است. اگر آنیل مبلغ جایزه را بین خود و بالا قسمت کند، او نقطهای بر مرز را برمیگزیند(اگر نقطه توی هاشور واقع شود معناش اینست که مقادیری پول در این میان هدر رفته است). انتخاب از میان نقاط موجود بر مرز مقرون بهصرفهگی را بازی با حاصلجمع صفر مینامیم، چراکه وقتی همانند شکل ۴.۵، نقطهی B را بهجای A انتخاب شود، مجموع خسارات آنیل و منفعت بالا به صفر میرسد( برای مثال آنیل در نقطهی B ۳۰۰۰ روپی کمتر از نقطهی A دارد، و بالا در نقطهی B ۳۰۰۰ روپی، و در A هیچ مبلغی دستش را نمیگیرد).
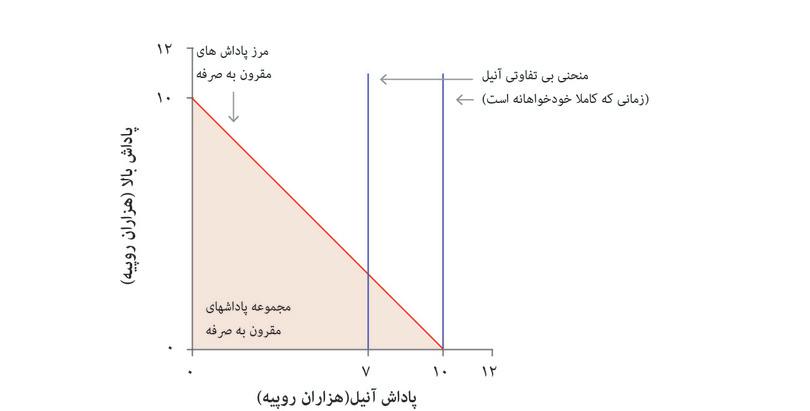
ترجیحات آنیل را میتوان با منحنیهای بیتفاوتی هم توضیح داد، که مجموع مبالغ آنیل و بالا را نشان میدهد که آنیل تمایلی برابر به همگیشان دارد. شکل ۴.۵ دو مورد را شرح میدهد: در اولی، آنیل تمایل دارد منفعت شخصی را دنبال کند پس منحنیهای بیتفاوتی او خطوط عمودی مستقیم هستند؛ در مورد دوم، مختصری تمایلات دیگرخواهانه دارد و نگران بالا است، پس منحنیهای بیتفاوتی او مایل به پایین اند.
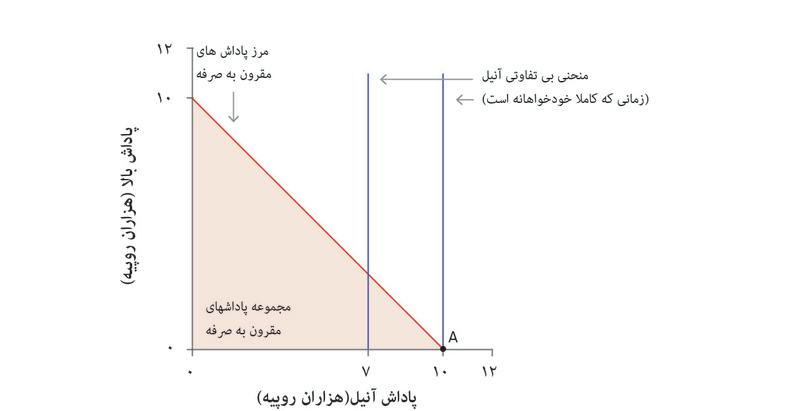
اگر آنیل آدم منفعتطلبی باشد، باتوجه به مجموعهی امکان پذیرش، بهترین گزینهی او نقطهی A است که براساس آن او همهی پول رابرای خودش برمیدارد. اگر از مصرف بالا نفعی ببرد، منحنیهای بیتفاوتی او به پایین میل میکنند، چنانکه ممکن است خروجیای را ترجیح دهد که درآن بالا هم سهمی از پول داشته باشد.
Leibniz: Finding the optimal distribution with altruistic preferences
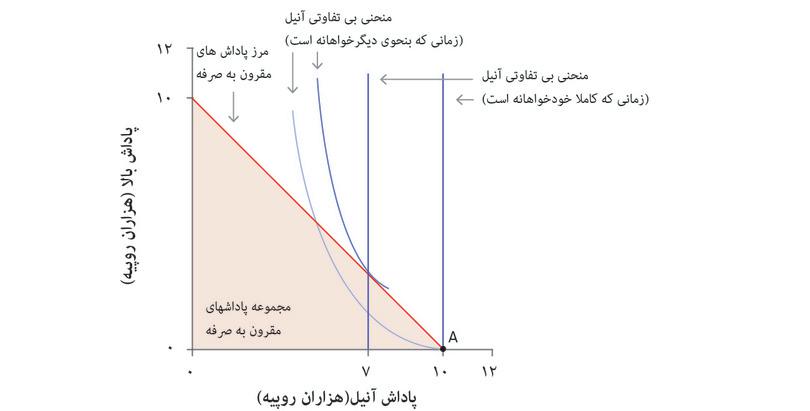
باتوجه به منحنیهای بیتفاوتیای که در شکل ۴.۵، آمدهاند، بهترین گزینهی مقرون بهصرفه برای آنیل نقطهی B است(۳.۷) که براساس آن ۷۰۰۰ روپیه را نگهداشته و ۳۰۰۰ تا به بالا میدهد. ترجیح آنیل این است که ۳۰۰۰ تا را به بالا بدهد، حتی اگر به قیمت ۳۰۰۰ روپیه برای خودش تمام شود. این نمونهای از دیگرخواهی است: آنیل حاضر است برای منفعت رساندن به کس دیگری هزینهای را متحمل شود. اگر تابع کارکردی دگرخواهانهی آنیل را مفروض گرفته و با چرتکه هم آشنا باشید، این لایبنیتز نشانتان خواهد داد که چگونه بهترین گزینهی امکانپذیر آنیل را پیدا کنید.
تمرین ۴.۳ دیگرخواهی و عدم خودخواهی
از منحنیهای شکل ۴.۵: استفاده کنید.
- اگر آنیل همانقدری به مصرف بالا اهمیت دهد که به مصرف خودش، منحنیهای بیتفاوتی او چه شکلی به خود خواهد گرفت؟
- و اگر او فقط از کل مصرف خود و بالا منتفع شود چه؟
- و اگر فقط از مصرف بالا منتفع شود چه؟
- برای هریک از این موارد تفسیری از تمایلات و ترجیحات آنیل به دست دهید.
پرسش ۴.۴ (یکی از پاسخها را انتخاب کنید)
در شکل ۴.۵ آنیل تازه بختآزمایی را برده و مبلغِ ۱۰۰۰۰ روپیه دریافت کرده است. او دارد سبکسنگین میکند که چه مقدار(اگر مقداری درکار باشد) از این مبلغ را با دوستش بالا قسمت کند. دیاگرامِ پایین مجموعه نتیجههایِ امکانپذیر را تصویر میکند، و نیز منحنیهایِ بیتفاوتیِ آنیل را نشان میدهد( برای وقتی که کاملا خودخواه است و هم برایِ وقتی اندکی دیگرخواه است). متاسفانه، پیش از آنکه آنیل بخواهد ترتیبِ تقسیمِ جایزهاش را بدهد، یک صورتحسابِ مالیاتیِ ۳۰۰۰ روپیهای برایِ جایزهاش دریافت میکند. براساسِ این اطلاعات، کدامیک از گزارههایِ زیر درست است؟
- بدونِ احتسابِ مالیات آنیل دقیقا ۳۰۰۰ روپیه را به بالا میداد. حالا با درنظرگرفتن درآمدِ کلِ ۷۰۰۰ روپیه، آنیل تصمیم خواهدگرفت که پولِ کمتری از این مبلغ را به دوستش بدهد.
- فرض میکنیم که تمایلات در اینجا ثابت هستند. بنابراین آنیل مختصری دیگرخواه باقی مانده و مقداری از جایزهاش را به بالا میبخشد.
- قبضِ مالیات را میتوان بهعنوان حرکت رو به داخلِ مرزِ مقرون بهصرفهگی مجسم کرد.لذا حدِمطلوب انتخاب آنیل برایِ او منجر به این میشود که نسبت به قبل در نقاط پایینتری از منحنی بیتفاوتی قرار گیرد
- بالا قبل و بعدِ رسیدنِ قبض به ترتیب ۱۰۰۰۰ و ۷۰۰۰ روپیه دریافتی میداشته است.
۴.۵ تمایلات دیگرخواهانه در تنگنای زندانی
وقتی آنیل و بالا خواستند از شر آفات خلاصی یابند(بخش ۴.۳)، خودشان را در یک تنگنای زندانی یافتند. یکی از دلایلی که خروجی نامطلوبی به بار آورد این بود که آنها نتایج کنشهای خود و هزینههای متحمل شده بر دیگری را بحساب نمیآوردند. انتخاب روش آفَتزدایی با استفاده از حشرهکش، دلالت بر یک مفتسواری بر مشارکت کشاورز دیگر در تامین آب تمیز داشت.
اگر آنیل به رفاه بالا نیز به اندازهی رفاه خودش اهمیت بدهد، خروجی حاصله میتواند متفاوت باشد.
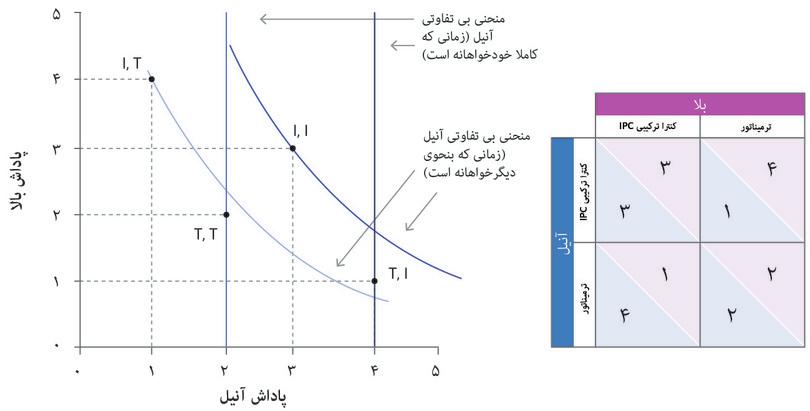
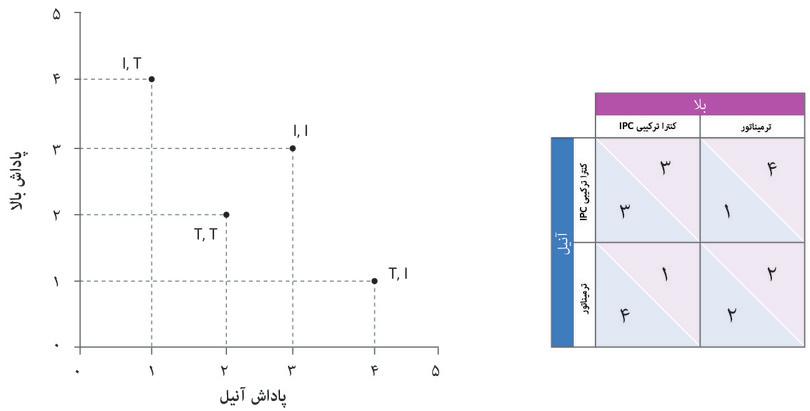
در شکل ۴.۶ دو محور اکنون نتیجههای آنیل و بالا را ارائه میدهند. درست مثل مثال بختآزمایی، نمودار نشاندهندهی خروجیهای امکانپذیر است. البته، مجموعهی امکانپذیر دراین مورد تنها چهار نقطه را شامل میشود. برای راحتی کار اسامی استراتژیها را کوتاه کردهایم: T بهجای ترمیناتور، I برای IPC . توجه داشته باشید که حرکات روبهبالا و نیز بهطرف راست از ( T، T) به سوی (I، I)، به خروجی بردـبرد میرسند: بیشترین میزان نتیجه برای هر دو.از سوی دیگر، حرکت به بالا، و به سمت چپ، یا پایین و به سمت راست ـ بهعبارتی از ( I، T) به ( T، I) یا بالعکس ـ تغییرات بردـباخت هستند. بردـباخت یعنی که بالا، به هزینهی آنیل، نتیجه بیشتری از آنیل نصیبش شود، یا آنیل به هزینهی بالا ، منتفع شود.
همانگونه که در مثال تقسیم پول بختآزمایی دیدیم، اینجا نیز دو مورد را بررسی میکنیم: اگر رفاه بالا برای آنیل مهم نباشد، منحنیهای بیتفاوتی او خطوط عمودی ازکار درمیآیند؛ و اگر به رفاه بالا اهمیت بدهد، منحنیهای بیتفاوتی او به پایین میل میکنند. برای اینکه ببینید در هر موردی چه پیش خواهد آمد، از خطوط جانبی استفاده کنید.
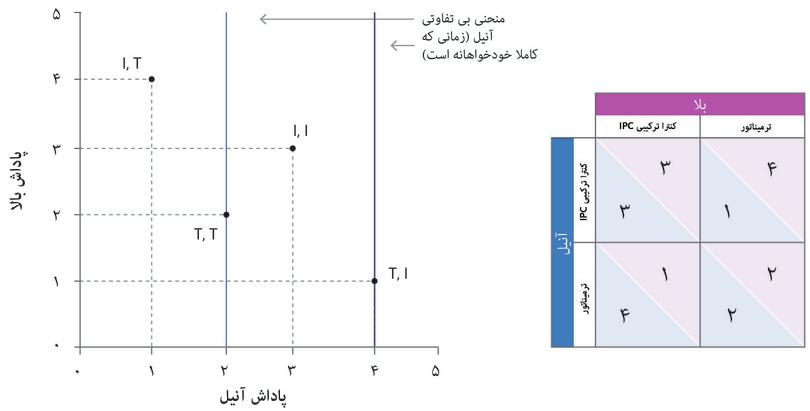
شکل ۴.۶ چنین برمیآید که وقتی آنیل کاملا خودـمنفعتطلب است، استراتژی مسلطش T خواهد بود(چنانکه پیشتر دیدیم). اما اگر آنیل بهحد کفایت نگران سرنوشت بالا باشد، آنوقت استراتژی مسلط او I است. اگر بالا هم حس مشابهی داشته باشد، آنوقت هردو IPC را انتخاب میکنند، و به این منجر به خروجیای میشود که اولویت اول آنهاست.
درس مهمی که از این مثالها باید بگیریم این است که اگر مردم دغدغهی یکدیگر را داشته باشند، عبور از تنگناهای اجتماعی به مراتب کار آسانتری خواهد بود. این مثالها همینطور در درک نمونههای تاریخیای که در آنها مردم متقابلا برای آبیاری یا وا داشتن پروتکل مونترال به محافظت از لایهی ازن دست به همکاری میزنند، و نمیخواهند که بر تعاون دیگران مفتـسواری کنند.
پرسش ۴.۵ (همهیِ پاسخهایِ صحیح را انتخاب کنید)
شکل ۴.۶ ترجیحات و تمایلاتِ آنیل را در مواقعِ دیگرخواهی و خودخواهیِ او نشان میدهد، و نیز وقتی که او و بالا در بازیِ تنگنایِ زندانی مشارکت میکنند.
عطفِ به این نمودار میتوان چنین گفت که:
- T,I ، نسبت به I,I رویِ یک منحنیِ بیتفاوتیِ یالاتر واقع میشود( که یعنی بیشتر به راست است) و T,T نسبت به I,T رویِ یک منحنیِ بیتفاوتیِ عمودیِ بالاتر واقع است. با این تفاسیر ترمیناتور در زمانِ خودخواهیِ کاملِ آنیل استراتژیِ مسلطِ اوست.
- وقتی آنیل مختصر احساسی از دیگرخواهی دارد، I,I نسبت به T,I رویِ کی منحنیِ بیتفاوتیِ بالاتر میافتد، و I,T هم رویِ منحنیِ بیتفاوتیِ بالاتری از T,T واقع میشود. لذا استعمالِ IPC استراتژیِ مسلطِ آنیل است.
- ترمیناتور برایِ هردو بازیکن استراتژیِ مسلط است، پس T,T یک توازنِ استراتژیِ مسلط است.تمایلِ آنیل به T,I است اما بالا هرگز IPC را انتخاب نمیکند.
- IPC در مواقعِ دیگرخواهیِ آنیل، استراتژیِ مسلطِ اوست. چنانچه بالا تمایلاتِ مشترکی داشته باشد، آنوقت IPC برایِ او نیز یک استراتژیِ مسلط خواهد بود، با این تفاسیر، I,I توازنِ استراتژیِ مسلط است.
تمرین ۴.۴ خودمنفعتطلبی غیراخلاقی
جامعهای را تصور کنید که درآن هرکسی سراسر درپی منفعت شخصی است (فقط و فقط به فکر دارایی شخص خودش است) و مسئولیت اخلاقیای متوجه خود نمیداند(هیچ قانون اخلاقی متداخل با دستیابی به آن ثروت را گردن نمینهد). چنین جامعهای چگونه از جامعهای که در آن زندگی میکنید متمایز است؟ موارد زیر را درنظر بگیرید:
- خانوادهها
- محلهای کار
- همسایهها
- ترافیک
- فعالیت سیاسی (آیا مردم رای خواهند داد؟)
۴.۶ کالاهای عمومی، مفتسواری و تعامل مکرر
حالا بیایید نگاهی بیاندازیم به دومین دلیلی که در بازی تنگنای زندانی ما را به خروجی نامطلوب هدایت میکند: هیچ راهی نبود که آنیل و بالا بتوانند فرد استفاده کننده از حشرهکش را برای خسارتی که زده مجبور به دادن غرامت کند.
مسائل آنیل و بالا مسائلی فرضی هستند، اما تنگناهای واقعی مفتسواری را در خود مستتر دارد، تنگناهایی که بسیاری از مردم در سرتاسر جهان با آنها مواجه میشوند. برای مثال، بهمانند اسپانیا، کشاورزان بسیاری در آسیای جنوب شرقی برای تولید محصول به یک وسیلهی آبیاری اشتراکی متکی هستند. این سیستم آبیاری نیازمند نگهداری مستمر و سرمایهگذاری جدید است. هر کشاورزی شخصا تصمیم میگیرد که چه سهمی در این فعالیتها داشته باشد. فعالیتهای مذکور کل جماعت را بهرهمند میسازد و اگر حتی کشاورز برای همکاری داوطلب نشود، باقی کشاورزان کار ار انجام خواهند داد.
تصور کنید که چهار کشاورز دارند تصمیم میگیرند که آیا در نگهداری پروژهی آبیاری شریک شوند یا نه.
- کالای عمومی
- کالایی که استفاده یک فرد از آن، در دسترس بودنِ آن برای دیگران را کاهش نمیدهد. همچنین تحت عنوان کالاهای فاقدِ-رقیب هم شناخته میشوند. همچنین نگاه کنید به: کالای عمومی غیرقابل مستثناسازی، کالای دارای کمیابی مصنوعی.
برای هریک از آنها هزینهی شرکت در پروژه ۱۰ دلار است. اما وقتی کشاورزی شرکت کند، همهی آن چهار تا از افزایشی که در نتیجه محصولشان حاصل میشود بهره میبرند، و این افزایش را آبیاری ممکن کرده است، لذا هریک از آنها ۸ دلار به جیب خواهد زد. شرکت در پروژهی آبیاری را یک کالای عمومی مینامند: وقتی یک فرد برای تهیهی کالا متقبل هزینهای بشود، همه از آن بهرهمند میگردند.
اکنون انتخابی که کیم، یکی از آن چهار کشاورز، با آن مواجه است را درنظر بگیرید. شکل ۴.۷ نشانمان میدهد که چگونه تصمیم او به کل دریافتی او بستگی دارد، اما همچنین به تصمیم کشاورزان دیگری بسته است که تصمیم به شرکت در پروژهی آبیاری میگیرند.
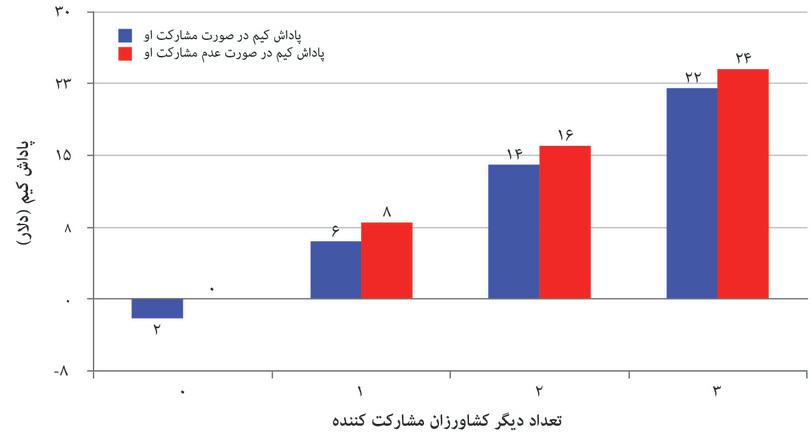
نتیجههای کیم در بازی کالای عمومی.
شکل ۴.۷ نتیجههای کیم در بازی کالای عمومی
مثالی بزنیم. اگر دونفر از دیگران شرکت کنند، یک سود ۸ دلاری از هریک از شراکتها عاید کیم میشود. پس اگر خودش شرکت نکند و سهیم نشود، نتیجه کل او، که با قرمز نشان داده شده، ۱۶ دلار است.اگر تصمیم به شرکت بگیرد، یک سود ۸ دلاری اضافی هم دریافت خواهد کرد( و این برای سه کشاورز دیگر هم صادق است).اما متحمل خسارتی ۱۰ دلاری هم میشود و لذا بازدهی کل او ۱۴ دلار است، چنانکه در شکل ۴.۷، دیدیم، و چنانکه در شکل ۴.۸محاسبه شده است..
| سود حاصله از شراکت دیگران | ۱۶ | |
| بهاضافهی سود حاصل از شراکت خود او | + | ۸ |
| منهای هزینهی شراکت او | – | ۱۰ |
| کل | ۱۴ دلار |
مثال: وقتی دو نفر از کشاورزان دیگر شرکت کنند، اگر کیم هم شراکت کند، بازدهی او کمتر خواهد بود.
شکل ۴.۸ مثال: وقتی دو نفر از کشاورزان دیگر شرکت کنند، اگر کیم هم شراکت کند، بازدهی او کمتر خواهد بود.
شکل ۴.۷ و شکل ۴.۸ تنگنای اجتماعی را شرح میدهد: کشاورزان تصمیم به انجام هر کاری که بگیرند، کیم اگر سهیم نشود و شرکت نکند پول بیشتری درمیآورد، تا وقتی که شریک شود. [بهعبارتی] شرکت نکردن یک استراتژی مسلط است. او میتواند بر شراکت دیگران مفتسواری کند.
بازی کالاهای عمومی یک تنگنای زندانی است که دران بیش از دو بازیکن درگیرند: اگر کشاورزان صرفا به بازدهی پولی خویش بیاندیشند، یک توازن استراتژی مسلط برقرار است که در آن هیچکس شرکت نمیکند و بازدهی همهی آنها صفر است. از طرف دیگر، اگر همه شرکت میکردند به هر یک از آنان ۲۲ دلار میرسید. همه نفع میبرند اگر همه شراکت کنند، اما صرفنظر از کنش دیگران، هرکشاورزی با مفتسواری بر شراکت دیگران نتیجهی بهتری خواهد گرفت.
دیگرخواهی میتواند به حل مسالهی مفتسواری کمک کند: اگر کیم به کشاورزان دیگر اهمیت میداد شاید به شراکت در پروژهی آبیاری علاقمند میشد. لیکن اگر شمار زیادی از مردم در یک بازی کالای عمومی درگیر باشند، احتمال اینکه دیگرخواهی برای تداوم بخشی به یک خروجی سودآور متقابل کفایت کند بسیار پایین خواهد بود.
بااینحال هنوز که هنوز است در جایجای جهان، کشاورزان و ماهیگیران در بسیاری از موارد با وضعیتهای اموال عمومی با موفقیت چشمگیری برخورد کردهاند. شواهدی که الینور استروم( Elinor Strom) و دیگر پژوهشگران دررابطه با پروژههای آبیاری اشتراکی، در هند، نپال و دیگر کشورها گرد آوردهاند، نشان میدهد که میزان این تعاون متغیر است. در برخی جماعات، تاریخی از اعتماد به این تعاون دامن میزند. در باقی، تعاون اتفاق نمیافتد. در جنوب هند برای مثال، روستاهایی که نابرابریهای مفرطی در زمین و جایگاه کاستی(طبقاتی) در آنها بیداد میکند، دررابطه با مصرف آب تضادهای بیشتری را تجربه میکردند. روستاهایی که نابرابری کمتری را شاهد بودند، سیستمهای آبیاری را بهنحو مناسبتری نگهداری کردهاند: بهعبارتی اینجا تداوم تعاون آسانتر بود.8
اقتصاددانان بزرگ الینور استروم
انتخاب الینور استروم(۲۰۱۲-۱۹۳۳)، دانشمند در سیاست، برای دریافت مشترک جایزهی نوبل اقتصاد در سال ۲۰۰۹ اغلب اقتصاددانان را شگفتزده کرد. برای مثال، استیون لویت پروفسور اقتصاد در دانشگاه شیکاگو، تصدیق میکند که چیزی دربارهی کار الینور نمیدانسته، و «بخاطر نمیآورد که او را دیده باشد و یا شنیده باشد که یک اقتصاددان نام او را بر زبان آورده باشد».
البته این انتخاب مدافعان سینهچاکی هم داشت. ورنون اسمیت یک اقتصاددان تجربی که پیش از این جایزه را برده بود، برای لحاظ کردن اصالت او، «عقل سلیم علمی» و اراده به گوش سپردن «دقیق به دادهها»، به کمیتهی نوبل تبریک گفت.
کل کار دانشگاهی استروم متمرکز بود بر مفهومی که اگرچه نقشی محوری در اقتصاد بازی میکند اما بندرت جزئیات آن بررسی شده است: مالکیت یا دارایی. رونالد کوز، اهمیت حقوق مالکیت مشخص و حقوق مرتبط با آنرا روشن کرده است(در مواقعی که کنشهای یک شخص آسایش دیگران را تحت تاثیر قرار میدهد). اما علاقهی اصلی کوز مرز میان فرد و دولت در تنظیم چنین کنشهایی است. استروم ناحیهی میانه را بررسی میکند که آنجا جماعات، و نه افراد یا حکومتهای رسمی، حقوق مرتبط به دارایی را در اختیار دارند.
خرد مرسوم در آن وقت این بود که مالکیت جمعی و غیررسمی منابع به یک «تراژدی منابع عمومی» ختم میشود. بدین معنا که، به باور اقتصاددانان تحت رژیم دارایی اشتراکی نمیتوان منابع را مداوما و به کفایت مورد استفاده قرار داد. باید به الینور استروم دستخوش بگوییم که این نگاه دیگر نگاه غالب نیست.
اولا، او تمایزی قائل شد میان منابعی که دارایی اشتراکی محسوب میشوند و آندسته منابعی که دسترسی به آنها آزاد است:
- دارایی اشتراکی مستلزم وجود یک جامعهی درست تعریف شده از کاربرانی است که قادر به عمل هستند، اگر نه تحت قانون، دستکم برای منع غیرخودیها از استثمار منابعشان. محلهای ماهیگیری ساحلی، چراگاهها و نواحی جنگلی نمونههای آن هستند.
- *منابع دسترسیـآزاد * ممکن است بدون اعمال محدودیت استثمار شوند، جدای آنهایی که دولتها به تنهایی یا متعاقب توافقات بینالمللی روی آن کار میکنند: برای نمونه محلهای صید ماهی در اقیانوس، یا اتمسفر زمین بهعنوان یک زبالهدان کربنی.
- هنجارهای اجتماعی
- درکی که برای غالب اعضای جامعه مشترک است و به آنها میگوید در شرایطی که کنشهایشان دیگران را متأثر میکند، چه کاری باید انجام دهند.
استروم در تاکید بر این تمایز تنها نبود، اما او ترکیب بینظیری از مطالعات موردی، روشهای آماری، مدلهای نظری بازی با جزییات نامعمول، و آزمایشها برای فهم این امر فراهم آورد که چگونه میتوان از تراژدیهای مشاعات دوری جست. او تنوعی عظیم را در سازوکار ادارهی دارایی اشتراکی کشف کرد. برخی جماعات قادر بودند قوانینی وضع کنند و برای حصول به هنجارهای اجتماعی منابع به آن متوسل شوند، حال آنکه بقیهی جماعات از انجام چنین کاری عاجز بودند. بیشتر عمر دانشگاهی او به تشخیص معیار موفقیت اختصاص یافت و به استفاده از نظریه برای درک اینکه چرا برخی روشها کارگر میافتادند و باقی نه.
بسیاری از اقتصاددانان بر این باورند که تنوع خروجیها را میتوان با بکارگیری نظریهی بازیهای مکرر درک کرد، که پیشبینی میکند که حتی در مواقعی که همهی افراد فقط به خودشان اهمیت میدهند، اگر کنشهای متقابل با احتمال بالا و بهشکل مناسبی تکرار شوند، افراد به اندازهی کافی صبور هستند، پس خروجیهای تعاونی برای مدتی نامحدود میتوانند پایدار باشند.
اما این برای استروم تببین راضیکنندهای نبود، قسمی به این خاطر که همان نظریه پیشبینی کرد که هر گونه خروجی، منجمله تورم سریع ، ممکن است سربرآورد.
و مهمتر از همه اینکه، استروم میدانست که استفادهی مدام را کنشهایی تضمین میکنند که بوضوح انحراف از فرضیهی مادی خودمنفعتطلبی است. بطور خاص، افراد باکمال میل هزینههای چشمگیری را متقبل میشوند تا زیرپا گذارندگان قانون یا هنجارها را تنبیه کنند. همانطور که پل رومر خاطر نشان میکند، او نیاز به بسط «مدلهای تمایلات بشری با وارد کردن یک نوعی تنبیه مشروط دیگران در آن» را تشخیص داده است.
استروم مدلهای نظری بازی ساده را توسعه داد، بازیای که درآن افراد تمایلات نامتعارفی دارند و مستقیما به اعتماد و نفع متقابل اهمیت میدهند. همچنین شیوههای مواجههی مردم با یک تنگنای اجتماعی را بررسی کرد، راههایی که مردم به توسط آنها و با تغییر قوانین بهگونهای که طبیعت استراتژیک تعامل دگرگون شد، توانستند از بروز تراژدی جلوگیری کنند.
او با اقتصاددانان دیگر برای راهاندازی یکسری آزمایشهای اولیه همکاری کرد، آزمایشهایی که استفادهی مرسوم از مجازات هزینهبر در پاسخ به استخراج مفرط منابع را تایید میکردند، و همچنین قدرت ارتباطات و نقش حیاتی توافقات غیررسمی در حمایت از تعاون را بر ما روشن کرد. توماس هابز یک فیلسوف قرن هفدهمی، اظهار داشته که توافقات بایستی توسط حکومت وضع شوند، چراکه «عهود، بدون شمشیر، فقط مشتی کلمهاند، و برای ایمن نگاه داشتن یک مرد هیچ نیرویی ندارند». استروم با او مخالف است. همانطور که در عنوان یک مقالهی تاثیرگذار مینویسد، عهود ـ حتی در غیاب شمشیرـ حکومت بر خویشتن را ممکن میکنند.9
ترجیحات اجتماعی تاحدی توضیح میدهند که چرا این جماعتها از تراژدی منابع عمومی هاردین اهتراز میکنند. اما همچنین ممکن است این جماعات شیوههایی برای جلوگیری از رفتار مفتسوارانه پیدا کنند.
بازیهای مکرر
مفتسواری امروز ما بر شانه مشارکت دیگر اعضای جامعه میتواند فردا یا سالها بعد پیامدهای نامطلوبی داشته باشد. روابط جاری یکی از ویژگیهای مهم تعاملات اجتماعی است که در الگویی که تا اینجای کار استفاده کردهایم، دیده نشده است: زندگی یک بازی یک نوبته نیست.
تعامل بالا و آنیل در مدل ما یک بازی یک نوبته بود. اما بهعنوان مالکان زمینهای همجوار، آنیل و بالا بهشکل واقعبینانهتری بایستی مکررا تعامل داشته باشند.
تصور کنید که سازوکار امور چقدر عوض میشد اگر که تعامل آنها را همچون یک بازی ارائه میدادیم که باید هر فصل تکرارش میکردند. فرض کنید که بالا IPC را برگزیده؛ دراینصورت بهترین پاسخ آنیل چیست؟ استدلال او چنین خواهد بود:
آنیل: من اگر IPC را بازی کنم آنوقت شاید بالا به استفادهی خود از IPC ادامه دهد، اما اگر ترمیناتور را به کار ببرم ـ که سود من را در فصل جاری افزایش میدهدـبالا سال بعد از ترمیناتور استفاده خواهد کرد. با اینتفاسیر و ازآنجایی که من بشدت برای درآمد کمصبرم، بهتر است که به IPC بچسبم.
بالا میتواند دقیقا استدلال مشابهی را پیش بکشد. نتایج ممکن است بهگونهای باشد که آندو پس از آن برای همیشه با IPC بازی کنند.
در بخش بعد نگاهی خواهیم داشت به شواهد آزمایشگاهی دررابطه بااینکه وقتی یک بازی کالاهای عمومی تکرار میشود، مردم چه رفتاری پیش خواهند گرفت.
پرسش ۴.۶ همهیِ پاسخهایِ صحیح را انتخاب کنید
چهار کشاورز درحالِ تصمیمگیری برایِ شرکت کردن یا نکردن در نگهداریِ پروژهیِ آبیاری هستند. هزینهیِ شراکت در پروژه برایِ هر کشاورز ۱۰ دلار است. اما زمانیکه هر کشاورزی همکاری کند، هر چهار تایِ آنها از یک افزایش در بازدهیِ محصولاتشان منتفع خواهند شد، درنتیجه هریک ۸ دلار بدست میآورد.
کدامیک از گزارههایِ زیر درست است؟
- عدمِ همکاری در پروژه برایِ تمامیِ کشاورزان یک استراتژیِ مسلط است: بقیه هر کاری بکنند، سودِ آنها از همکاری ۸ دلار است، ولی هزینه ۱۰ دلار.
- دراینمورد او ۱۶ دلار از این شراکت به جیب میزند، که از رقمِ هزینه بیشتر است.
- سوایِ کاری که کیم میکند، استراتژیِ مسلط برایِ یک کشاورزِ خودخواه عدمِ همکاری خواهد بود.
- اگر رابطهای میانِ این کشاورزان جاری باشد، همهیِ آنها ممکن است همکاری کنند تا از سودِ حاصله از تعاونِ مدام بهرهمند شوند. اگر هریک از همسایگان نتواند یکسال در پروژه شریک شود، این تعاون متلاشی خواهد شد. آنها با اشراف به این نکته، میلِ شدیدی به شرکت در زمانِ حال خواهند داشت.
۴.۷ مشارکت در امور عمومی و مجازات متناسب با آن
آزمایشها ثابت میکنند که مردم میتوانند سطح بالایی از تعاون در یک بازی کالای عمومی را حفظ کنند، مشروط به اینکه اگر همکاری کمتر از حد معمول کسی ثابت شد، فرصتهایی برای گیرانداختن مفتسواران داشته باشند.
شکل ۴.۹الف نتایج حاصل از آزمایشی در یک لابراتوار را نشان میدهد که هزینهها و سود حاصل از همکاری در یک کالای عمومی را در دنیای واقعی تقلید کرده است. آزمایشها را در شهرهایی در اقصی نقاط جهان به انجام رساندند. شرکتکنندگان در هرآزمایش یک بازی اموال عمومی ۱۰ رانده را بازی کردند، مشابه با بازیای که کیم و سه کشاورز دیگر در آن درگیر بودند. در هر راند، افراد حاضر در آزمایش ( که آنها را سوژه میخوانیم) ۲۰ دلار دریافت میکنند. آنها بهشکلی تصادفی به گروههای کوچک نوعا ۴ نفرهای سرشکن میشوند که یکدیگر را نمیشناسند. از آنها خواسته میشود که از ۲۰ دلار خود به یک صندوق مالی اشتراکی کمک کنند. صندوق یک کالای عمومی است: به ازای هر دلار کمک، هر عضو گروه، و از جمله خود کمککننده ۰.۴۰ دلار گیرش میآید.
تصور کنید که شما دارید بازی میکنید و انتظار شما اینست که سه عضو دیگر گروه شما هریک ۱۰ دلار کمک کند. بااین تفاسیر شما درصورت عدم همکاری ۳۲ دلار خواهید گرفت ( شامل سه بازگشت ۴ دلاری از همکاری بقیه، بهعلاوهی ۲۰ دلاری که در ابتدای کار نگه داشتهاید). بقیه هرکدام ۱۰ دلار کمک رساندهاند، لذا هریک فقط ۲۲ دلار دریافت میکنند (۱۰-۳۲). از طرف دیگر، اگر شما هم ۱۰ دلار خود را کمک کنید، آنوقت هرکسی، منجمله شما، با عدم همکاری به نتیجهی بهتری میرسید ـ بهموجب آنکه پاداش مفتسواری (۳۲ دلار) بیش از عدم همکاری است (۲۶ دلار). و از بخت بد شما این نکته درباره دیگر اعضای گروه شما هم صدق میکند.
بعد از هر دور بازی، میزان همکاری اعضای دیگر گروه با مشارکین درمیان گذاشته میشود. در شکل ۴.۹الف، هر خط دگرگونی میانگین همکاریها در مکانهای متفاوتی در سرتاسر جهان را ارائه میدهد. عینا همانگونه که در تنگنای زندانی دیدیم، اینجا نیز مشخص است که مردم صرفا خودمنفعتطلب نیستند.
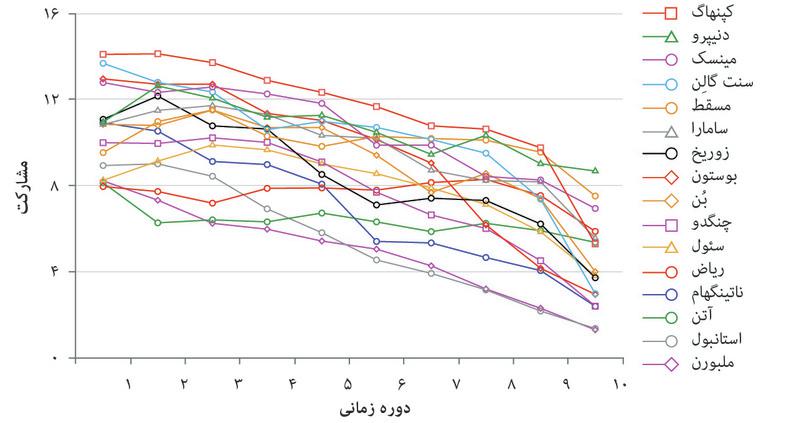
آزمایشهای مرتبط با کالای عمومی در سرتاسر جهان: میزان همکاری در ۱۰ دوره.
شکل ۴.۹الف آزمایشهای مرتبط با کالای عمومی در سرتاسر جهان: میزان همکاری در ۱۰ دوره.
Benedikt Herrmann, Christian Thoni, and Simon Gachter. 2008. ‘Antisocial Punishment Across Societies’. Science 319 (5868): pp. 1362–67.
همانطور که مشاهده میکنید، کشاورزان چنگدو در راند اول ۱۰ دلار کمک میکنند( عینا مانند مثال فوقالذکر). در هر جمعیتی که بازی در آن جریان داشته باشد، کمکهای اعطایی به کالای عمومی در دور اول بازی بالاتر هستند، هرچندکه این واقعیت در برخی شهرها( کپنهاگن) بیشتر از باقی(ملبورن) صادق است. این مطلب شایان توجه است: اگر شما تنها نگران بازدهی خود باشید، در آنصورت استراتژی مسلط شما عدم همکاری صرف خواهد بود. کمکهای بالای اولیه میتواند بهاین خاطر روی داده باشد که شرکتکنندگان حاضر در آزمایشها همکاری خود را با توجه به بازدهیهای دیگران به انجام رساندهاند( بهعبارتی دیگرخواه بودهاند). مشکل (یا به بیان هاردین، تراژدی) اما بهقوت خود باقی است: همه جا همکاری برای حفظ اموال عمومی طی زمان کاستی میگیرد.
بااینوجود، نتایج همچنین حاکی از این است که علیرغم تغییر بزرگی که میان جوامع هست، اغلب آنها در انتهای آزمایش، کماکان سطوح همکاری بالایی از خود نشان میدهند.
اما مشخص است که دیگرخواهی تبیین منطقی این الگو نیست. احتمال دارد که کمککنندگان سطح همیاری خود را کاهش دهند، اگر مشاهده کنند که دیگران کمتر از حد انتظار کمک میکنند و بر آنها مفتسواری میکنند. چنین به نظر میرسد که آنها که بیش از میانگین کمک میکنند، خواهان مجازات اینگونه افراد مفتسوار هستند، بخاطر بیانصافی یا انحراف از هنجار اجتماعی همکاری هستند. ازآنجایی که بازدهی مفتسواران به کل همکاری در حفظ کالای عمومی بستگی دارد، لذا تنها راه مجازات مفتسواران در آزمایش مذکور جلوگیری از شرکت آتی آنهاست. و این تراژدی مشاعات است. بسیاری از مردم مادامی که بقیه به نفع متقابل اهمیت دهند، از همکاری خوشحال میشوند. برآورده نشدن این انتظار علت قانعکنندهی اصلی برای افت تدریجی بازیکنان در راندهای بعدی این بازی است.
برای آزمودن فرض فوق، آزمایشگران بازی آمده در شکل ۴.۹الف را گرفتند و یک گزینهی مجازات در آن وارد کردند. پس از مشاهدهی همکاریهای گروه خود، بازیکنان میتوانند با مجبور کردن بازیکنان خاطی مبلغی برای تنبیه آنها بپردازند، اینطوری میتوانند یک غرامت ۳ دلاری دریافت کنند. مجازاتگر بازی گمنام باقی میماند، اما مجبور است برای مجازات هر بازیکنی 1 دلار بپردازد. نتیجه در شکل ۴.۹ب. آمدهاست. اکثریت سوژههای آزمایش، منجمله در چین، کرهی جنوبی، اروپای شمالی و کشورهای انگلیسیزبان، وقتی مجال مجازات مفتسواران را داشتند، سطح همکاری آنها نیز افزایش یافت.
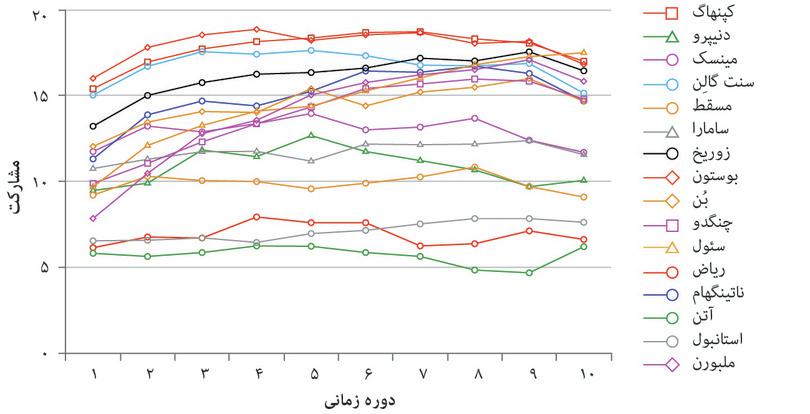
آزمایشهای مربوط به کالای عمومی با فرض وجود فرصت مجازات برابر
شکل ۴.۹ب آزمایشهای مربوط به کالای عمومی با فرض وجود فرصت مجازات برابر
Benedikt Herrmann, Christian Thoni, and Simon Gachter. 2008. ‘Antisocial Punishment Across Societies’. Science 319 (5868): pp. 1362–67.
مردمی که فکر میکنند دیگران نامنصف بودهاند یا پا روی هنجاری اجتماعی گذاشتهاند، ممکن است تلافی کنند، حتی اگر هزینهی اینکار برایشان بالا باشد. مجازات دیگران بهدست آنها شکلی از دیگرخواهی است، زیراکه آنها برای جلوگیری از رفتار مفتسوارانه ـ که برای آسایش بیشتر اعضای گروه زیانبخش است ـ متقبل هزینهای میشوند.
این آزمایش روشن میکند که حتی در گروههای بزرگ مردمی، با ترکیبی از کنشهای متقابل مکرر و تمایلات اجتماعی، میتوان سطوح بالای همکاری در حفظ اموال عمومی را حفظ کرد.
بازی کالای عمومی، همچون تنگنای زندانی، وضعیتی است که در آن هرکسی با پیوستن به دیگران در پروژهای مشترک( مثل کنترل آفات، نگهداری یک سیستم آبیاری، یا کنترل نشر کربن ) چیزی گیرش میآید. اما همچنین چیزی از کف میدهد اگر دیگران مفتسواری کنند.
۴.۸ آزمایشهای رفتاری در آزمایشگاه و در میدان
برای درک رفتار اقتصادی نیازمند شناخت تمایلات مردم هستیم. برای مثال در فصل قبل زمان آزاد برای دانشجویان و کشاورزان ارزش داشت. میزان ارزشگذاری آنها بخشی از اطلاعات مورد نیاز ما برای پیشبینی اینکه آنها چه مدت زمانی را به مطالعه یا کشاورزی اختصاص میدهند.
- ترجیح آشکارشده
- شیوهای برای مطالعه ترجیحات ازطریق مهندسی معکوسِ انگیزههای یک فرد (یا ترجیحاتِ او) از روی مشاهداتی درباره کنشهای آن فرد.
در گذشته اقتصاددانان اطلاعات خود دربارهی تمایلات اجتماعی را از راههای زیر بدست میآوردند:
- سؤالات پیمایشی: برای تشخیص تمایلات سیاسی، وفاداری به کالایی خاص، میزان اعتماد دیگران، یا جهتگیریهای مذهبی.
- مطالعات آماری رفتار اقتصادی: برای مثال، خرید یک یا چند کالا وقتی قیمت نسبی متغیر است ـ برای تعیین تمایلات موجود به کالایی مورد بحث. یک استراتژی مهندسی معکوس تمایلات فرضی است، چنانچه خریدها آنها را آشکار میکنند. این را ترجیح آشکارشدهمیگوییم.
در رابطه با پیمایشها مشکلی وجود دارد: اگر از کسی بپرسیم که آیا بستنی دوست دارد، یحتمل پاسخ صادقانهای دریافت خواهیم کرد. اما پاسخ به سؤال «شما چهاندازه دیگرخواه هستید؟»، ممکن است آمیزهای از حقیقت، خودتبلیغی، و افکار مشتاقانه از کار درآید مطالعات آماری نمیتوانند محیط تصمیمگیری را کنترل کنند، محیطی که درآن تمایلات آشکار میشوند، از اینرو مقایسهی انتخابهای گروههای مختلف کار دشواری است.
اقتصاددانان بهایندلیل گاهی از آزمایش استفاده میکنند که میتوان رفتار مردم را تحت شرایط کنترل شده به مشاهده درآورد.
چگونه اقتصاددانان از دادهها میآموزند آزمونهای آزمایشگاهی
آزمونهای رفتاری در مطالعات تجربی تمایلات تبدل به عنصری مهم شدهاند.10 بخشی از انگیزهی انجام آزمایشها این است که درک انگیزههای یک شخص(دیگرخواهی، تمایل به نفع متقابل، مخالفت با نابرابری و خودـمنفعتطلبی) نقشی ضروری در توان پیشبینی ما از رفتار مردم بهعنوان کارمند، عضو خانواده، حافظان محیط زیست و شهروند دارد.
آزمونها بیشتر کردههای مردم را میسنجند تا گفتههاشان را. آزمایشها تا سرحدامکان باید طراحی واقعبینانهای داشته باشند و درعینحال وضعیت را کنترل کنند:
- تصمیمات تبعاتی دارند: تصمیمات گرفتهشده در یک آزمایش ممکن است مشخص کند که سوژهها با تقبل نقش چقدر پول بدست میآورند. گاهی مخاطرات موجود ممکن است به اندازهی درآمد یکماه فرد است.
- دستورالعملها، مشوقها و قوانین برای همهی سوژهها مشترک هستند: همچنین رفتار با سوژهها باید یکسان باشد. این بدان معناست که اگر قصد مقایسهی دو گروه را داشته باشیم، تنها تفاوت موجود بین گروه کنترل و گروه رفتار خود همین طرز برخورد است، بطوریکه تاثیرات آن قابل تشخیص هستند.
- آزمایشها را میتوان تکرار کرد: آنها بهگونهای طراحی میشوند که با دیگر گروههای مشارکین نیز قابل اجرا باشند.
- آزمایشها تلاش دارند تبیینهای ممکن دیگر را هم کنترل کنند: باقی متغیرها تا آنجا که ممکن است ثابت نگهداشته میشوند، چراکه ممکن است رفتار مورد سنجش ما را تحت تاثیر قرار دهند.
این بدین معنی است که وقتی مردم در آزمایش رفتار متفاوتی پیشه میکنند، شاید علتش تفاوت در تمایلاتشان باشد.
اقتصاددانان وسیعا به مطالعهی اموال عمومی پرداختهاند، با استفاده از آزمایشهایی که در آن میتوان از سوژهها خواست که تصمیماتی دررابطه با همکاری در حفظ یک کالای عمومی اتخاذ کنند. در مواردی، اقتصاددانان آزمایشهایی طراحی کردهاند که بهشکلی دقیق تنگناهای اجتماعی دنیای واقعی را بازسازی کردهاند. محض نمونه میتوان از کار خُوان کامیلو کاردناس اقتصاددانی در یکی از دانشگاههای کلمبیا یاد کرد. وی آزمایشهایی در باب تنگناهای اجتماعی و با مردمی به انجام رسانده که با مسائل مشابهی در زندگی واقعی خود روبرو هستند، از قبیل بهرهبرداری بیامان از یک جنگل یا ذخایر ماهی. در این ویدیو او استفادهی خود از اقتصاد آزمایشی در وضعیتهای واقعی زندگی را توصیف میکند، و توضیح میدهد که آزمایشها چگونه در فهم این نکته به ما یاری میرسانند که چرا مردم حتی زمانی که دلایل مبرهنی برای تعاون و همیاری ندارند، بازهم اینکار را میکنند.
اقتصاددانان کشف کردهاند که شیوهی رفتاری مردم در آزمایشها را میتوان برای پیشبینی واکنش آنها در وضعیت زندگی واقعی به کار برد. برای مثال، ماهیگیران برزیلی که همیاری بیشتری در یک بازی آزمایشگاهی داشتند، ماهیگیری را بهنحو پایدارتری نسبت به ماهیگیرانی انجام میدادند که در آزمایش همیاری کمی داشتند.
برای یافتن خلاصهای از انواع آزمایشات به انجام رسیده، نتایج حاصلهی اصلی، و اینکه آیا رفتار رخداده در آزمایشگاه میتواند رفتار در زندگی واقعی را پیشبینی کند یا خیر، نک به پژوهشی که برخی اقتصاددانان با تخصص اقتصاد آزمایشگاهی انجام دادهاند: برای مثال، کولین کامرر و ارنست فهر،10 آرمین فالک و جیمز هکمن،11 یا آزمایشاتی که ژوزف هنریش و تیم بزرگی از همکارانش در جهان انجام دادهاند. 12
بااین حال در تمرین ۴.۵ استیون لویت و جان لیست این سؤال را طرح میکنند که آیا مردم در خیابان به همان شیوهای رفتار میکنند که در آزمایشگاه؟
پرسش ۴.۷ (همهیِ پاسخهایِ درست را انتخاب کنید)
طبقِ نظرِ‘خوان کامیلو، اقتصاددانی که در ویدیو دیدی, اقتصاددانان با کاربردِ آزمایشهایی که سناریوهایِ کالایِ عمومی را شبیهسازی میکنند، کدامیک از مواردِ زیر را کشف کردند؟
- این یکی از یافتههایی است که پروفسور کاردناس ذکر میکند.
- پروفسور کاردناس درمییابد که جمعیتهایِ با نابرابریِ بیشتر اعتماد و همیاریِ کمتری از خود نشان میدهند.
- رفتارِ همیارانه حتی در مواقعی که پولِ واقعی(مثلِ آزمایشاتِ پروفسور کاردناس) به مشارکینِ آزمایش داده شود پدیدار میشود.
- این یکی از یافتههایِ موردِ اشارهیِ پروفسور کاردناس است.
تمرین ۴.۵ آیا آزمایشات آزمایشگاهی همیشه اعتبار دارند؟
استیون لویت و جان لیست به سال ۲۰۰۷ مقالهای منتشر کردند تحت عنوان آزمایشهای آزمایشگاهی سنجشگر تمایلات اجتماعی چه چیز جهان واقعی را آشکار میسازند.( برای دانلود روی لینک کلیک کنید. منابع بیشتری نیز در بخش بیشتر بخوانید در انتهای این فصل خواهید یافت).
1. چرا و چگونه ممکن است که رفتار مردم در زندگی واقعی متفاوت از رفتار مشاهده شده در آزمایشگاه باشد؟13
2. با استفاده از آزمایش کالاهای عمومی در این بخش، توضیح دهید که چرا امکان مشاهدهی تفاوتهای سیستماتیک بین مشاهدات ثبت شده در شکل ۴.۹الف و ۴.۹ب،وجود دارد، و اینکه در زندگی واقعی چه اتفاقی رخ خواهد داد.
مواقعی وجود دارد که میتوان آزمایشها را «در میدان» هدایت کرد: بهاینمعنا که، برای تغییر عامدانهی وضعیتهای اقتصادیای که مردم ذیل آنها تصمیمگیری میکنند، و نیز برای مشاهدهی اینکه رفتار آنها چگونه تغییر میکند. آزمایشی که درسال ۱۹۹۸ در اسراییل انجام شد، ثابت میکند که تمایلات اجتماعی ممکن است درقبال زمینهای که در آن تصمیمات اتخاذ میشوند، بسیار حساس و شکننده باشند.
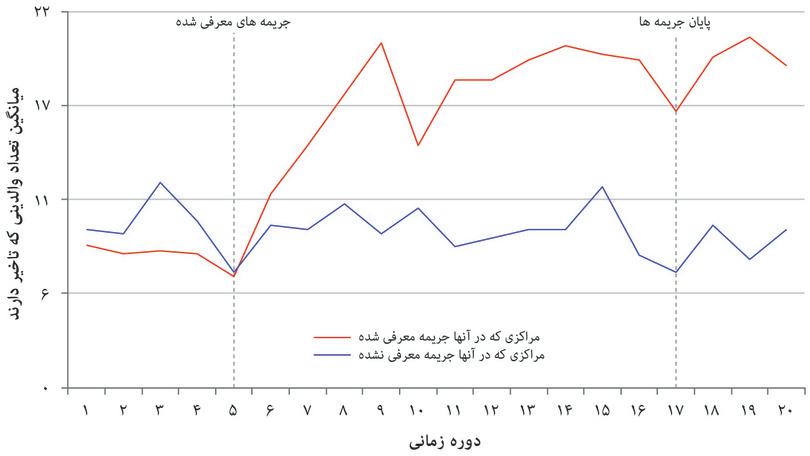
معمول است که والدین برای برداشتن بچهها از مهدکودک عجله به خرج میدهند. گاهی برخی والدین دیر میکنند، و این معلمان را وامیدارد مدت زمان اضافهای بهمانند. برای بازداشتن والدین از تاخیر چه میکنید؟ دو اقتصاددان آزمایشی ترتیب دادند که درآن در برخی از مهدکودکها( و نه در بقیه، که از آنها بهعنوان گروه کنترل استفاده شد)، جریمهای برای تاخیر تعریف شده بود. «هزینهی تاخیر» از صفر تا ده شِکِل اسرائیلی (سه دلار تقریبا)تعیین شد. مایهی شگفتی است که پس از وارد کردن جریمه به آزمایش، فراوانی تاخیرها دو برابر شد. خط بالایی در شکل ۴.۱۰ این وضعیت را به تصویر میکشد.
میانگین تعداد والدین تاخیردار
شکل ۴.۱۰ میانگین تعداد والدین تاخیردار
Uri Gneezy and Aldo Rustichini. 2000. ‘A Fine Is a Price’. The Journal of Legal Studies 29 (January): pp. 1–17.
چرا جریمه تاخیر نتیجه میدهد؟ یکی از تبیینهای ممکن این است که پیش از وارد کردن جریمه، اغلب والدین سر موقع میآمدند زیرا حس میکردند کار درست همین است. بهعبارت دیگر، آنها سروقت میآمدند چونکه برای زحمت ندادن به کارمندان مهدکودک یک الزام اخلاقی در خویش حس میکردند. شاید یک نگرانی دیگرخواهانه درمورد کارمندان داشتند، یا برداشتن سروقت بچه از مهدکودک را نوعی مسئولیتپذیری متقابل در مراقبت همزمان از بچه میدانستند. اما وضع جریمه نشان از آن داشت که وضعیت واقعا بیشتر به خرید کردن شباهت دارد. تاخیر بهایی داشت و لذا، مثل سبزی یا بستنی، قابل خریدوفروش بود.14
- خلوتکردن
- این واژه دو کابرد کاملاً مجزا دارد. یک معنا، تأثیرِ منفی مشاهدهشده در هنگامی است که مشوقهای اقتصادی جای انگیزههای اخلاقی و دیگر انگیزههای دیگرخواهانهی افراد را میگیرند. در مطالعاتِ رفتار فردی، مشوقها میتوانند اثرِ خلوتکننده یا غربالکنندهای بر ترجیحات اجتماعی داشته باشند. کاربرد دوم این واژه اشارهای به تأثیرِ افزایشِ هزینهکردِ دولتیِ در کاهش هزینهکردِ خصوصی است، چنانکه مثلاً در اقتصادی که با بالاترین ظرفیتِ کارائی فعالیت میکند، یا هنگامی که افزایش نرخ بهره زمینهساز توسعه پولی میشود، مشاهده میکنیم.
استفاده از یک مشوق بازاری ـ هزینهی تاخیرـ آنچه روانشناسان «چارچوب» جدید تصمیمگیری مینامند را برای والدین فراهم میآورد، یعنی تصمیمات را بهگونهای برمیگرداند که درآنها خودمنفعتطلبی حاکم است تا اهمیت دادن به دیگران. وقتی جریمهها و هزینهها چنین تاثیرات ناخواستهای دارد، میگوییم که مشوقها تمایلات اجتماعی را پراکندهاند. بدتر اینکه، از شکل ۴.۱۰ میتوانید دریابید که پس از حذف جریمه نیز والدین [کماکان] به دیر برداشتن بچههایشان ادامه دادند.
پرسش ۴.۸ ( یک پاسخ را انتخاب کنید)
شکل ۴.۱۰ عددِ میانگینِ والدینِ تاخیردار در هفته را در مهدکودکها به تصویر میکشد، برایِ برخی از مهدها جریمه تعریف شده و برایِ بقیه خیر. چنانکه در نمودار معلوم است، جریمهها در نهایت حذف شدند.
براساسِ این اطلاعات، گزارهیِ درست را انتخاب کنید:
- نمودار نشان میدهد که شمارِ والدینِ تاخیردار در مراکزی که جریمه درآنها تعریف شده، بیش از دوبرابر شد.
- والدین تنها درصورتِ تاخیر جریمه را میپرداختند، پس میتوان جریمه را بهایِ تاخیر محسوب کرد.
- نمودار نشان میدهد که شمارِ والدین تاخیردار پس از حذفِ جریمه همچنان بالا ماند، بنابراین امکانِ این وجود دارد که آزمایش برخوردار از تاثیری ثابت و پایدار بوده است.
- پسراندنِ تمایلاتِ اجتماعی زمانی پدیدار میشود که التزامِ اخلاقی به دیرنیامدن، جایِ مشوقِ شبهـبازاریِ خریدِ حقِ تاخیر بدونِ تردید اخلاقی را بگیرد. نمودار بهوضوح این وضعیت را بلافاصله پس از وضعِ جریمهها به تصویر میکشد.
تمرین ۴.۶ خلوت کردن
تصور کنید که شهردار شهری کوچک هستید و میخواهید شهروندانتان را به مشارکت در مراسم روز شهر زیبا تشویق کنید که در آن مردم یک روز را به تمیز کردن پارکها و جادهها سپری میکنند.
چه برنامههایی برای آنروز ترتیب میدهید تا مردم انگیزه به مشارکت پیدا کنند؟
۴.۹ همیاری، مذاکره، تضاد منافع و هنجارهای اجتماعی
- همیاری
- مشارکت در یک پروژه مشترک که معطوف به ایجاد عواید متقابل است.
همیاری (تعاون) به معنای مشارکت در پروژهای اشتراکی و به طریقی است که منفعت دوجانبه رخ بدهد. نیازی نیست که همیاری بر یک توافق بنا شود. تا اینجا مثالهایی دیدهایم که درآنها افراد کنشگر مستقل کماکان میتوانند به یک خروجی همیارانه برسند:
- دست نامرئی: بالا و آنیل محصول خود را با تعقیب منفعت شخص خود انتخاب کردند. توافق آنها در بازار دِه به یک تقسیم کار سودآور دوجانبه ختم شد.
- تنگنای زندانی مکرر: آنها ممکن است از به کاربردن ترمیناتور برای کنترل آفَت خودداری کنند، زیرا خسارات آتی وارده را بهعنوان نتیجهی کنارگذاشتن IPC تشخیص میدهند.
- بازی کالای عمومی: ارادهی بازیکنان به مجازات دیگران، سطوح بالای همیاری را در بسیاری از کشورها پایدار نگاه داشت، و هیچ نیازی به توافق مشاهده نشد.
در موارد دیگر، از قبیل تنگنای زندانی یک نوبته، کنشهای مستقل به خروجی نامطلوبی منتهی شدند. ازاینرو بازیکنان در صورت رسیدن به یک توافق، نتایج بهتری میگرفتند.
مردم معمولا برای حلوفصل مسائل اجتماعی و اقتصادی خود به مذاکره متوسل میشوند. برای مثال، مذاکرهی بینالمللی به پروتکل مونترال منجر شد، که در خلال آن کشورها برای منع استفاده از کلروفلوروکربنها و به هدف جلوگیری از یک خروجی آسیبزا(نابودی لایهی ازن) با یکدیگر به توافق رسیدند.
مذاکره اما همیشه کنشی نتیجهبخش نیست، و گاهی علت آن بروز تضاد منافع است دررابطه با چگونگی تقسیم عواید همیاری. برای همین است که گاهی میبینیم، توفیق پروتکل مونترال،در کاهش انتشار کربن که گرمای زمین را بدنبال داشته، مقایسه میشود با شکست نسبی پروتکل کیوتو. علل امر تاحدی علمی هستند: فناوریهای جایگزین کلروفلوروکربنها ( CFCs) پشرفته بودند و نسبت بهره به هزینه برای کشورهای بزرگ صنعتی، از قبیل ایالات متحده، بسیار خالصتر و بزرگتر از موارد مرتبط با انتشار گازهای گلخانهای بود. لیکن یکی از موانع توافق در نشست تغییرات اقلیمی ۲۰۰۹ کپنهاگن این مساله بود که سود و هزینههای این تحدید انتشار چگونه باید بین کشورهای توسعهمند و درحال توسعه تقسیم شود.
مثال سادهتری از تضاد منافع: یک استاد دانشگاه را مجسم کنید که قصد دارد دانشجویی را بهعنوان دستیار پژوهشی خود در تابستان استخدام کند. در اصل، هردوی آنها از این رابطه چیزی بدست میآورند، زیرا ممکن است فرصت خوبی برای هم یادگیری و هم پول درآوردن دانشجو باشد. علیرغم ظرفیت موجود برای نفع دوجانبه، همچنین فضایی برای تضاد نیز در این رابطه وجود دارد. استاد ممکن است بخواهد پول کمتری بپردازد و اعظم پول دریافتی خود را به خرید رایانهای نو اختصاص دهد، یا شاید باید سریعا کار را تحویل بدهد، و این یعنی که دانشجو وقت آزادی نخواهد داشت. پس از مذاکره، آنها ممکن است سازش کنند و توافق کنند که دانشجو دریافتی کمتری داشته باشد و درعوض دورکاری کند و در نهایت شاید مذاکره به شکست بیانجامد.
وضعیتهای اینچنینی بسیاری در اقتصاد وجود دارد. مذاکره( که گاهی چانهزنی هم خوانده میشود) همچنین بخشی از سیاست، امور خارجه، حقوق، زندگی اجتماعی و حتی دینامیک خانوادگی است. پدر و مادری ممکن است یک موبایل هوشمند به بچهشان بدهند تا بهجای گذراندن عصری بیسروصدا با آن بازی کند، یک کشور ممکن است زمینی را درعوض صلح بدهد، یا حکومتی ممکن است بخواهد با دانشجویان معترض و بخاطر ثبات سیاسی خودش اندکی به مذاکره تن بدهد. چنانکه در مثال استاد و دانشجو دیدیم، هریک از این چانهزنیها، درصورت عدم ارادهی طرفین ممکن است واقعا اتفاق نیافتد.
مذاکره: تسهیم عواید دوجانبه
برای کمک به درک سازوکار یک معامله، وضعیت زیر را درنظر بگیرید. شما و یکی از دوستانتان در خیابانی خلوت قدم میزنید و یک اسکناس ۱۰۰ دلاری روی زمین پیدا میکنید. تصمیم شما برای تقسیم این پول بادآورده چیست؟ اگر پول را دقیقا دو قسمت کنید، شاید اینکار شما دال بر هنجاری اجتماعی در جامعهی شماست که به شما میگوید بادآورده را باد میبرد و باید۵۰-۵۰ تقسیمش کرد.
تقسیم یک چیز حاوی ارزش به دو قسمت برابر (قانون ۵۰-۵۰) در بسیاری جماعات یک هنجار اجتماعی است، همانطور که هدیه دادن به اعضای خانواده و رفقای نزدیک در روز تولد نیز یک هنجار است. هنجارهای اجتماعی میان کل گروههای مردم مشترک هستند (تقریبا همه از آنها تبعیت میکنند)، و به شخص میگویند که در انظار مردم جامعهی خود چه کاری باید انجام دهد.
در اقتصاد وقتی از مردمی حرف میزنیم که برطبق تمایلات خود تصمیم میگیرند، منظورمان همهی تمایلات، عدم تمایلات، مواضع و باورهایی است که آنها را برمیانگیزد. بااین تفاسیر تمایلات هرکسی فردی هستند: ممکن است تحت تاثیر هنجارهای اجتماعی واقع شوند، اما کنشهای مطلوب مردم را به همان خوبی بازتاب میدهد که کنشهای اخلاقی لازمالاجرای آنها را.
انتظار ما این خواهد بود که حتی به فرض وجود یک هنجار ۵۰-۵۰ در جماعتی، ممکن است برخی افراد احترام درستی به هنجار نگذارند. برخی ممکن است خودخواهتر و دیگران سخاوتمندتر از آنی باشند که هنجار ایجاب میکند. اتفاقات بعدی نه تنها به هنجارهای اجتماعی (فاکتی دربارهی جهان، که نمایانگر مواضع موجود درقبال برابری است و طی دورههای طولانی شکل گرفته)، بلکه همچنین به تمایلات ویژهی افراد درگیر بستگی دارد.
- انصاف
- شیوهای از ارزیابیِ یک تخصیص برمبنای درکِ فرد از عدالت.
فرض کنید که شخصی که اول پول را دیده آنرا برمیدارد. دستکم سه دلیل برای بخشیدن بخشی از آن به یک دوست وجود دارد:
- دیگرخواهی: این علت را اخیرا در مورد بالا و آنیل بررسی کردیم.این شخص ممکن است دیگرخواه باشد و به آسایش آن دیگری و یا جوانب دیگری از رفاه او اهمیت بدهد.
- انصاف: یا، شخص دارندهی پول ممکن است فکر کند که ۵۰-۵۰ عادلانه است. دراین مورد، انگیزهی شخص، عدالت، یا به قول اقتصاددانان نفرت از نابرابری است.
- دوطرفهبودن یا همنفعی: رفیق قصهی ما ممکن است درگذشته با کسی که پول را یافته، مهربان بوده باشد، یا کلا آدم مهربانی است، و لایق آن است که رفتار سخاوتمندانهای با او در پیش گرفته شود. دراین مورد میگوییم که پولیاب ما برخوردار از تمایلات همنفعی است.
تمامی این تمایلات اجتماعی برخی اوقات رفتار مار را خلاف جهت متاثر میکنند. برای مثال،اگر شخص یابندهی پول تمایلات قوی برابرخواهانه دارد، اما میداند که دوستش کاملا خودخواه است، تمایلات برابرخواهانهی او را به تقسیم پول، و همـنفعخواهی او را به نگهداشتن پول وسوسه میکنند.
پرسش ۴.۹ (همهیِ پاسخهایِ درست را انتخاب کنید)
سرگرمیِ موردِعلاقهیِ آناستازیا و بلیندا فلزیابی است. ازقضا روزی آناستازیا چهار سکهیِ رُمی پیدا میکند و سرِ بلیندا بیکلاه میماند. هر دو زن تمایلاتِ همـنفعانه یا دوطرفه دارند. عطف به این اطلاعات میتوان گفت که:
- بستگی به میزانِ دیگرخواهیِ آناستازیا دارد. او میتواند دیگرخواه بوده اما فقط یک سکه به بلیندا بدهد.
- چون آناستازیا همـنفعخواه است، ممکن است بخواهد بلیندا را برایِ خودخواهیِ او درگذشته تنبیه کند. لذا حتی اگر دیگرخواه هم باشد، باز شاید از تنبیه رضایتِ بیشتری حاصل کند تا از تقسیم.
- همـنفعخواهی به معنایِ آنست که آناستازیا در صورتِ بهرهمندی از دیگرخواهیِ بلیندا درگذشته یا امید به بهرهمند شدن از آن در آینده، کماکان راضی به قسمت کردنِ پول خواهد بود.
- دیگرخواهیِ آناستازیا و تمایلِ او به حرکت نکردن برخلافِ جهتِ سنجهیِ برابریِ بلیندا -بهگونهای که مجازات نشود ـ ممکن است برایِ تشویقِ او به تقسیمِ ۵۰-۵۰ پول کفایت بکند یا نکند.
۴.۱۰ تقسیم کیک (یا روی میز گذاشتن آن)
یکی از متداولترین ابزارهای مطالعهی تمایلات اجتماعی بازی یک نوبته دونفرهای است بهنام بازی اولتیماتوم. این بازی در جایجای جهان با سوژههایی شامل دانشجویان، کشاورزان، کارگران انبارهای کالا، شکارچیان به انجام رسیده است. ما با مشاهدهی گزینههای آنها تمایلات و انگیزههای سوژهها را بررسی کردهایم( از قبیل خودمنفعتطلبی صرف، دیگرخواهی، مخالفت با نابرابری، یا همنفعخواهی).
سوژههای آزمایش دعوت به یک بازی میشوند که درآن مقادیری پول خواهند برد. مقدار پولی که میبرند به چگونگی بازی آنها و دیگران بستگی دارد. پول واقعی در بازیهای آزمایشگاهی اینچنینی در خطر قرار دارد، وگرنه نمیتوان اطمینان حاصل کرد که پاسخهای سوژهها به یک سؤال فرضی آیا کنش آنها در زندگی واقعی را منعکس میکند یا نه.
قوانین بازی برای بازیکنان شرح داده میشوند. طی یک یارکشی تصادفی دوبهدو جفت میشوند، بعد دوباره بهشکل تصادفی به یک بازیکن نقش پیشنهاددهنده، و به دیگری نقش پاسخگو داده میشود. سوژهها یکدیگر را نمیشناسند، اما میدانند که بازیکن دیگر هم مثل خودشان برای آزمایش استخدام شده است. سوژهها گمنام میمانند.
برش چنین شکلی بخود میگیرد: x دلار برای تو، y دلار برای من، آنجاکه: x + y = ۱۰۰. پاسخگو میداند که پیشنهاددهنده ۱۰۰ دلار برای تقسیم کردن دارد. پس از مشاهدهی پیشنهاد، پاسخگو یا آنرا میپذیرد یا رد میکند. اگر پیشنهاد رد شود، هیچیک از افراد چیزی بدست نمیآورند. اگر پذیرفته شود، قسمت کردن پول به انجام میرسد: پیشنهاددهنده x دلار و پاسخگو y دلار بدست میآورند. برای مثال، اگر پیشنهاددهنده پیشنهاد ۳۵ دلاری بدهد و پاسخگو بپذیرد، آنوقت پیشنهاددهنده ۶۵ دلار و پاسخگو ۳۵ دلار بدست میآورند. اگر پاسخگو پیشنهاد را رد کند، چیزی عایدشان نخواهد شد.
این را یک پیشنهاد رد-یا-قبول مینامند.اتمام حجت و التیماتوم در نام آن مستتر است. پاسخگو با یک گزینه مواجه است: پذیرش ۳۵ دلار، یا به جیب زدن هیچ.
- بهره اقتصادی
- هرگونه پرداخت یا سایر مزایایی که فرد بالاتر و علاوه بر آنچه در بهترین گزینه بعدی خود (یا گزینه ذخیره خود) بدست میآورد، بدست آورده باشد. همچنین نگاه کنید به: گزینه ذخیره
این بازی، یک بازی دربارهی تسهیم بهرهی اقتصادی ای است که در تعامل پدیدآمده است. یک کارفرما که میخواهد تکنولوژی جدیدی وارد کند میتواند بهره ـ سود بیشتری که نسبت به تکنولوژی کنونی بدست خواهد آوردـ را با کارمندان قسمت کند، البته اگر در وارد کردن آن سهیم شوند. اینجا، بهره بالا میکشد، چون آزمایشگر عجالتا کلوچه را در اختیار پیشنهاددهنده گزارده تا قسمتش کند. اگر مذاکره به نتیجه برسد( پاسخگو پیشنهاد را بپذیرد)، بهرهای عاید هر دو بازیکن خواهد شد( یک تکه کلوچه)؛ بهترین گزنیهی جایگزین بعدی برای هردو بدست آوردن هیچ است( کلوچهها دور ریخته میشوند).
در مثال فوق، چنانچه پاسخگو پیشنهاد را بپذیرد، سپس پیشنهاددهنده یک بهرهی ۶۵ دلاری عایدش میشود، و پاسخگو ۳۵ دلار میگیرد. نهگفتن برای پاسخگو هزینهای در بر دارد. بهرهی مقرر را میبازد. بنابراین هزینهی فرصت رد پیشنهاد در اینجا ۳۵ دلار است.
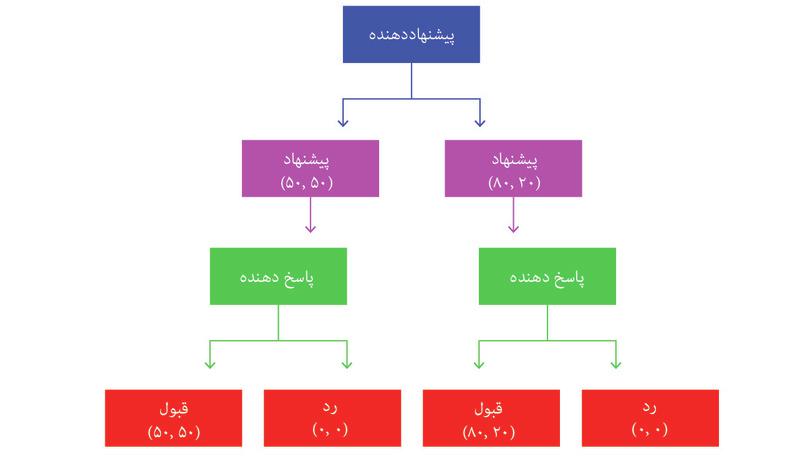
ما کار را با اندیشیدن به نمونه ساده شده ای از بازی التیماتوم آغاز کردیم، که در شکل ۴.۱۱ در نموداری باعنوان درخت بازی ارائه شده است. گزینههای پیشنهاددهنده یا پیشنهاد منصفانهی یک سهم برابر است،۵۰-۵۰ در شکل، یاپیشنهاد غیرمنصفانهی ۲۰ دلاری(نگهداشتن ۸۰ تا برای خودش). لذا پذیرش یا رد پیشنهاد تنها گزینهی پاسخگو است. بازدهیها در ردیف آخر آمدهاند.
درخت بازی برای بازی التیماتوم
شکل ۴.۱۱ درخت بازی برای بازی التیماتوم
- بازی ترتیبی
- بازیای که در آن همه بازیگران استراتژیهای خود را همزمان انتخاب نمیکنند، و بازیگرانی که بعداً انتخاب میکنند، امکان مشاهده استراتژیهای پیشاپیش انتخابشده توسط دیگر بازیگران را ببینند، مثلاً بازی اولتیماتوم. همچنین نگاه کنید به بازی همزمان.
درخت بازی شیوهی کارآمدی برای نمایاندن کنشهای متقابل اجتماعی است زیرا روشن میکند که چه کسی، چه کنشی انجام میدهد، وقتی انتخابی میکند، و نتایج حاصلهی کنش او چیستند. مشاهده میکنیم که در بازی التیماتوم اول یک بازیکن (پیشنهاددهنده)، و بهدنبال او پاسخگو، استراتژی خود را انتخاب میکنند. این [وضعیت] را بازی ترتیبی مینامند؛ پیشتر نگاهی داشتیم به بازیهای همزمان، که درآنها بازیکنان استراتژیهای خود را توامان انتخاب میکنند.
- بازیهای همزمان
- بازیای که در آن بازیگران استراتژیهای خود را همزمان انتخاب میکنند، مثلاً بازی تنگنای زندانی. همچنین نگاه کنید به بازی ترتیبی.
عایدی پیشنهاددهنده به کنش پاسخگو بستگی دارد، ازاینرو پیشنهاددهنده مجبور است به پاسخ احتمالی بازیکن دیگر بیاندیشد. بههمین دلیل هم هست که این [ملاحظهکاری] را تعامل استراتژیک مینامند. اگر شما پیشنهاددهنده هستید، نمیتوانید پیشنهاد ناچیزی را مطرح کنید، تا ببینید که چه رخ خواهد داد: شما فقط یک شانس برای پیشنهاد دادن دارید و نه بیشتر.
خودتان را در این بازی جای پاسخگو بگذارید. آیا (۵۰-۵۰ ) را میپذیرید؟ (۸۰-۲۰ ) را چطور؟ حالا نقشها را عوض کنید. فرض کنید که پیشنهاددهنده هستید. چه سهمی به پاسخگو پیشنهاد میدهید؟ آیا پاسخ شما به هویت بازیکن دیگر بستگی دارد؟( یک دوست ، یک غریبه، یک شخص نیازمند، یا یک رقیب).پاسخگویی که فکر میکند پیشنهاد پیشنهاددهنده هنجار اجتماعی برابری را زیرپاگذاشته، یا پیشنهاد به گمانش بهنحو تحقیرآمیزی ناچیز مینماید، شاید بخواهد بازدهی خود را قربانی تنبیه پیشنهاددهنده کند.
اکنون به مورد اصلی برگردیم که درآن پیشنهاددهنده میتواند هرمبلغی بین ۰ و ۱۰۰ دلار را مطرح کند.اگر شما پاسخگو باشید، کمینهی مبلغی که حاضر به پذیرش آن هستید چقدر است؟ اگر پیشنهاددهنده باشید، چه مبلغی را پیش مینهید؟
- کمترین پیشنهاد قابلقبول
- در بازی اولتیماتوم، پائینترین پیشنهاد از طرف پیشنهاددهنده که از سوی پاسخگو رد نخواهد شد است. عموماً در وضعیتهای چانهزنی، برای اشاره به کممطلوبترین پیشنهادی که موردقبول واقع خواهد شد بکار میرود.
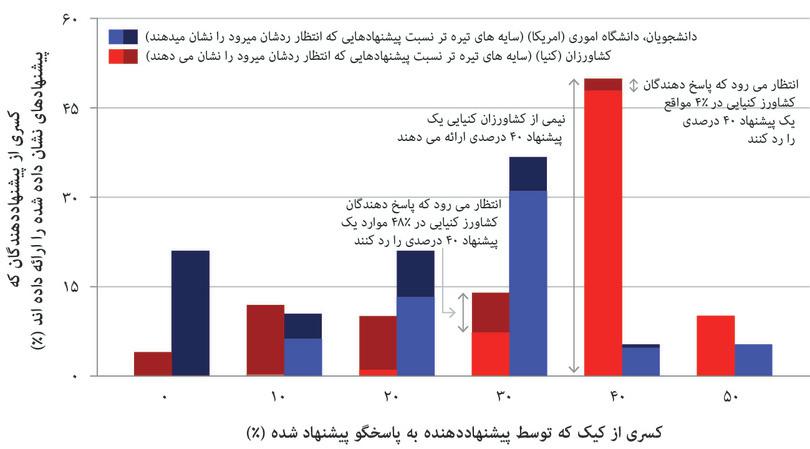
اگر با انیشتین در انتهای بخش کار کنید و تمرین ۴.۷ را که بهدنبال آن آمده را حل کنید،خواهید دید که کمترین پیشنهاد قابلقبول، با به حساب آوردن هنجارهای اجتماعی و موضع خود فرد در قبال همنفعی، چطور بدست میآید.کمینه پیشنهاد پذیرفتنی، پیشنهادی است که در آن لذت حاصل از بدست آوردن پول، همسنگ رضایت خاطری است که از رد پیشنهاد و بدست نیاوردن پول نصیب شخص میشود، اما همچنین در آن پاسخگو برخوردار از توان تنبیه پیشنهاددهنده برای زیرپا گذاردن هنجار اجتماعی ۵۰-۵۰ است. اگر شما پاسخگو باشید و کمینه پیشنهاد پذیرفتنی برای شما ۳۵ دلار است( از کل کلوچهی ۱۰۰ دلاری)، و اگر پیشنهاددهنده پیشنهاد ۳۶ دلاری به شما بدهد، ممکن است زیاد از پیشنهاددهنده خوشتان نیاید، اما کماکان، بهجای تنبیه او با رد پیشنهاد، پیشنهاد او را میپذیرید. در صورت رد پیشنهاد، با رضایت خاطری که ۳۵ دلار میارزد، و بی هیچ پولی به خانه خواهید رفت، درحالیکه میتوانستهاید ۳۶ دلار نقد به جیب بزنید.
اینشتین یک پیشنهاد در بازی التیماتوم چه زمانی پذیرفته خواهد شد؟?
فرض کنید که ۱۰۰ دلار هست که باید تقسیم شود، و یک هنجار برابری ۵۰-۵۰ هم برقرار است. درصورتیکه پیشنهاد ۵۰ دلار یا بیشتر باشد (y ≥ 50)، پاسخگو حس میکند که با پیشنهاد خوبی از جانب پیشنهاددهنده روبرو شده و طبیعتا آن را میپذیرد، چراکه رد آن، هم او و هم پیشنهاددهندهای که قدرش را میداند میرنجاند، چرا که آنها هنجار اجتماعی را رعایت کرده و حتی بیش از آن سخاوتمند بودهاند. اما اگر پیشنهاد زیر ۵۰ دلار باشد، آنوقت او حس میکند که هنجار ۵۰-۵۰ بخوبی رعایت نشده و شاید بخواهد پیشنهاددهنده را بهخاطر این سرباز زدن تنبیه و مجازات کند. درصورتیکه پیشنهاد را رد کند، متقبل هزینهای خواهد شد: رد کردن به معنای آن است که هردوی آنها هیچ پولی بدست نمیآورند.
فرض کنید که خشم پاسخگو از نقض هنجار اجتماعی، به اندازهی آن نقض و هنجارشکنی بستگی دارد: اگر پیشنهاددهنده چیزی پیشنهاد ندهد او از کوره در خواهد رفت، اما به احتمال قویتر در مواجهه با یک پشنهاد ۴۹.۵۰ دلاری بیشتر مبهوت میشود تا عصبانی، چراکه براساس هنجار اجتماعی انتظار ۵۰ دلار را داشته است. بااین تفاسیر میزان رضایت خاطری که از تنبیه پیشنهاد کم پیشنهاددهنده نصیبش خواهد شد، بستگی دارد به دو چیز: انگیزهی خصوصی همـنفعخواهی او (R)، و نفع او از پذیرش پیشنهاد (Y). R عددی است که به شدت انگیزهی خصوصی همـنفعخواهی پاسخگو اشاره دارد: درصورتیکه R عدد بزرگی باشد، آنوقت اینکه آیا پیشنهاددهنده کنش منصفانه و سخاوتمندانهای در پیش گرفته یا خیر، برای او اهمیت بسیار بیشتری پیدا خواهد کرد. اما اگر R=0 ، آنوقت او اصلا نگران انگیزههای پیشنهاددهنده نخواهد بود. پس میزان رضایتخاطر از رد یک پیشنهاد کم R(۵۰-y) خواهد بود. عایدی حاصل از پذیرش پیشنهاد هم خود پیشنهاد خواهد بود، یا همان y.
تصمیمگیری در رابطه با رد یا پذیرش پیشنهاد تنها بستگی به این دارد که کدامیک از این دو کمیت بزرگتر باشند. این رابطه را میتوان چنین نوشت: پیشنهاد را رد کن اگر y < R(۵۰ − y). این معادله میگوید که او پیشنهاد کمتر از ۵۰ دلار را رد خواهد کرد، برحسب اینکه پیشنهاد چه مقدار از ۵۰ دلار کمتر است( برحسب (۵۰-y))، ضربدر موضع شخصی او در قبال همـنفعخواهی(R).
برای محاسبهی کمینه پیشنهاد پذیرفتنی او میتوانیم معادلهی رد پیشنهاد فوق را از نو اینگونه تنظیم کنیم:
R=۱ بهاین معنی است که پاسخگو برای همـنفعخواهی و هنجار اجتماعی اهمیت یکسانی قائل است. اگر R=۱ ، پس y< ۲۵ و او هرگونه پیشنهاد کمتر از ۲۵دلار را رد خواهد کرد. نقطهی برش ۲۵دلار آنجایی است که دو انگیزهی نفع پولی و تنبیه پیشنهاددهنده دقیقا میزان و بالانس شدهاند: اگر او پیشنهاد ۲۵دلاری را پس بزند، ۲۵دلار میبازد اما ازآنطرف ۲۵ دلار هم میگیرد که همان ارزش رضایت خاطر او از تنبیه پیشنهاددهنده است، و پس بازدهی کل او صفر دلار خواهد بود.
پاسخگو هرچه بیشتر به همـنفعخواهی اهمیت بدهد، پیشنهاددهنده مجبور است پیشنهادهای بالاتری بدهد. برای مثال، اگرR=۰.۵، پاسخگو پیشنهادهای زیر ۱۶.۶۷ ((y<۱۶.۶۷) )را رد خواهد کرد، اما اگر R=۲، درآنصورت پاسخگو هر پیشنهاد زیر ۳۳.۳۳ را رد میکند.
تمرین ۴.۷ پیشنهادهای پذیرفتنی
- چگونه ممکن است که کمینه پیشنهاد پذیرفتنی (y) به روش بدستآوردن ۱۰۰ دلار بستگی داشته باشد(مثلا، آیا در خیابان یافته، در بختآزمایی برده، بهعنوان ارث دریافت کرده، یا…)؟
- فرض کنید که هنجار برابری و انصاف در این جامعه۵۰-۵۰ است. آیا میتوانید شخصی را در چنین جامعهای به تصور درآورید که پیشنهاد بالای ۵۰ درصد را مطرح کند؟ اگر چنین است، علت آن چیست؟
۴.۱۱ کشاورزان منصف، دانشجویان خودمنفعتطلب
اگر شما در یک بازی التیماتوم نقش پاسخگویی را داشته باشید که صرفا به بازدهی خود میاندیشد، باید هرگونه پیشنهاد مثبتی را بپذیرید، و مهم نیست که چقدر کوچک باشد، چراکه لنگه کفش کهنه در بیابان نعمت است! بنابراین، در جهانی که فقط از افراد خودـمنفعتطلب تشکیل یافته، پیشنهاددهنده پیشبینی میکند که پاسخگو هر گونه پیشنهادی را خواهد پذیرفت، و بههمین دلیل، کمینه مبلغ ممکن را مطرح خواهد کرد: یک سِنت، و با اشراف به اینکه حتما پذیرفته خواهد شد.
آیا این پیشبینی با دادههای آزمایشگاهی جور درمیآید؟ خیر، نمیآید. همانگونه که در تنگنای زندانی هم بود، اینجا نیز اگر مردم کاملا خودمنفعتطلب باشند، شاهد خروجی پیشبینی شده نخواهیم بود. بهعبارتی پیشنهادهای یک سِنتی رد خواهند شد.
برای مشاهدهی اینکه کشاورزان کنیایی و دانشجویان آمریکایی چگونه این بازی را پیش برند، نگاه کنید به شکل ۴.۱۲. ارتفاع هر میله نشانگر سهم پاسخگویانی است که میخواستند پیشنهاد نشاندادهشده بر محور افقی را بپذیرند. چنانکه انتظار میرفت، پیشنهادات بیش از نصف کلوچه برای همهی سوژهها در هردو کشور پذیرفتنی بود.
همیشه هم وضع بدین ترتیب نیست. در آزمایشهای انجام گرفته در پاپوآ در گینهی نو، پیشنهادهای بیش از نیم کلوچه معمولا توسط پاسخگویان رد شدند. اینجا پاسخگویان ترجیح میدانند چیزی بدست نیاورند و درعوض در یک خروجی بسیار ناعادلانه شریک نشوند، حتی اگر مطلوب آنها باشد، یا ترجیحشان این بود که دِین اجتماعی دریافت هدیهای بزرگ را متحمل نشوند، چراکه تقسیم آن وکشیدن منفعت متقابل از آن دشوار است. سوژهها مخالف نابرابری بودند، حتی وقتی که نابرابری موردبحث آنها را منتفع میکرد.15
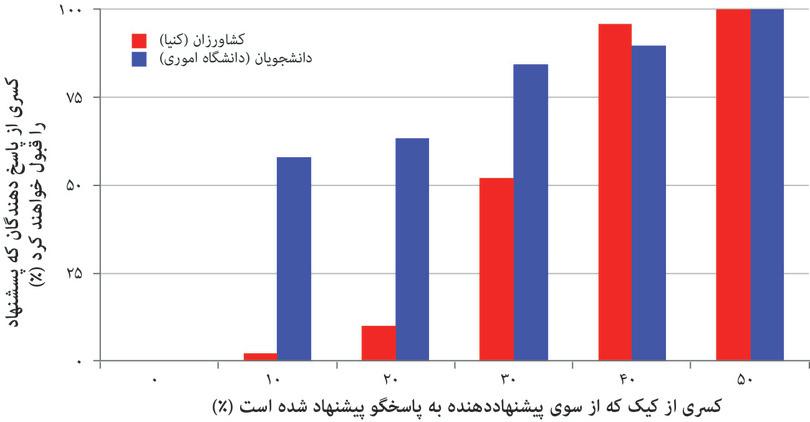
پیشنهادهای پذیرفتنی در بازی التیماتوم
شکل ۴.۱۲ پیشنهادهای پذیرفتنی در بازی التیماتوم
Adapted from Joseph Henrich, Richard McElreath, Abigail Barr, Jean Ensminger, Clark Barrett, Alexander Bolyanatz, Juan Camilo Cardenas, Michael Gurven, Edwins Gwako, Natalie Henrich, Carolyn Lesorogol, Frank Marlowe, David Tracer, and John Ziker. 2006. ‘Costly Punishment Across Human Societies’. Science 312 (5781): pp. 1767–1770.
توجه داشته باشید که کشاورزان کنیایی تمایل چندانی به پذیرش پیشنهادهای پایین ندارند، بلکم این باعث شود آنها را نامنصف بخوانید، حالآنکه دانشجویان آمریکایی تمایل بیشتری به پذیرش چنین پیشنهاداتی دارند. برای مثال، تقریبا تمامی کشاورزان(۹۰ درصد) به پیشنهاد یکـپنجم کلوچه(پیشنهاددهنده ۸۰ درصد کلوچه را نگه میدارد)، نه خواهند گفت، حالآنکه ۶۳ درصد دانشجویان چنین پیشنهاد ناچیزی را میپذیرند. بیش از نیمی از دانشجویان ۱۰ درصد کلوچه را میپذیرند، اما تقریبا هیچیک از کشاورزان آنرا نخواهد پذیرفت.
این درست که نتایج آمده در شکل ۴.۱۲ اشاره به آن دارند که مواضع موجود در قبال آنچه منصفانه است، تغییر میکند، و با تمامی اهمیتی که این انصاف دارد، هیچکس در آزمایشهای انجام گرفته در کنیا و آمریکا حاضر به پذیرش پیشنهاد صفر نبود، ولو اینکه با رد آن هم همان صفر نصیبشان خواهد شد.
تمرین ۴.۸ تمایلات اجتماعی
تجربه توصیف شده در شکل ۴.۱۲:را نظر بگیرید.
- بهنظر شما کدامیک از تمایلات اجتماعی مورد بحث در بالا، ارادهی سوژهها به رد پیشنهادات پایین( بااینکه با چنین کاری عملا چیزی بدست نخواهند آورد) را برانگیخته است؟
- بهنظر شما علت تفاوت کشاورزان کنیایی از دانشجویان آمریکایی چه بود؟
- بازی توصیف شده در این بخش را با استفاده از دو سری بازیکن مجزا انجام دهید: اول با همکلاسیها و بعد با خانواده و دوستانتیان در بیرون کلاس. آیا تفاوتی در پاسخهای دو گروه مشاهده میکنید؟ توضیح دهید.
ارتفاع کلی هر میله در شکل ۴.۱۳ به درصد پیشنهاددهندگان کنیایی و آمریکایی اشاره دارد، که پیشنهادهای آمده بر محور افقی را مطرح کردهاند. برای مثال، نیم کشاورزان پیشنهاد ۴۰ درصدی دادهاند. ۱۰ درصد دیگر تقسیم برابر را پیشنهاد دادهاند. فقط ۱۱ درصد دانشجویان چنین پیشنهادهای سخاوتمندانهای را مطرح کردهاند.
اما آیا کشاورزان واقعا سخاوتمند بودند؟ برای پاسخ به این پرسش شما مجبورید نه تنها به مبالغ پیشنهادی آنها، بلکه همچنین باید به استدلال احتمالی آنها بیاندیشید وقتی که پذیرش یا رد پیشنهاد از جانب پاسخگو را بررسی میکردهاند. اگر به شکل ۴.۱۳ نگاهی انداخته و بر کشاورزان کنیایی تمرکز کنید، خواهید دید که فقط عدهی قلیلی با پیشنهاد صفر خواستهاند کل کلوچه را برای خود نگه دارند( ۴ درصد آنها، چنانکه در میلهی سمت چپی میبینید)، و همینطور تمامی آن پیشنهادها رد خواهند شد( تمام میله تیره است).
از سوی دیگر، اگر به منتهیالیه سمت راست شکل نگاهی بیاندازیم، میبینیم که دررابطه با کشاورزان، پیشنهاد نیم کلوچه، یک نرخ پذیرش ۱۰۰ درصدی را تضمین میکند( تمام میله روشن است).کسانی که پیشنهاد ۳۰ درصدی دادند، به یک احتمال مساوی، درآستانهی مشاهدهی رد یا پذیرش پیشنهاد خود بودند( قسمت تیرهی میله تقریبا به بزرگی قسمت روشن آن است).
پیشنهاددهندهای که تاسرحد ممکن میخواست پول به جیب بزند، دو راه بیشتر نخواهد داشت: بدستآوردن همهی آن، یا تقسیم برابر آن را. کشاورزانی که پیشنهاد ۴۰ درصدی دادند، به احتمال بسیار قوی پیشنهادشان را مورد پذیرش مییافتند و ۶۰ درصد کلوچه را دریافت میکردند. در آزمایش مذکور، نصف کشاورزان پیشنهاد ۴۰ درصد را برگزیدند. انتظار ما این خواهد بود که تنها در ۴ درصد مواقع پیشنهادها با عدم پذیرش مواجه شوند، همانگونه که از بخش تیرهرنگ میله در قسمت پیشنهاد ۴۰ درصد در شکل ۴.۱۳ هم پیداست.
اکنون تصور کنید که شما یک کشاورز کنیایی هستید و تنها چیز مهم برای شما بازدهی خود شماست.
پیشنهاد هیچ دادن به پاسخگو در اینجا محلی از اعراب ندارد، زیراکه با چنین کاری و درصورت رد پیشنهاد از جانب پاسخگو، چیزی دست شما را نمیگیرد. مطرح کردن پیشنهاد نصف کلوچه[ اما]، مطمئنا نصف کلوچه را به شما میرساند ـ زیرا پاسخگو حتما آن را خواهد پذیرفت.
اما شما هنوز مرددید که میتوانستید عملکرد بهتری داشته باشید.
پیشنهاددهندهای که تنها به پاداشهای خودش اهمیت میدهد، چیزی را مقایسه خواهد کرد که پاداشهای موردانتظار از دو پیشنهاد مینامیم: و عبارتست از، میزان بازدهی مورد انتظار یک فرد، بادرنظر گرفتن کنش احتمالی شخص دیگر( رد یا پذیرش) در زمان طرح پیشنهاد. بازدهی انتظاری شما آن بازدهیای است که در صورت پذیرش بدست میآورید، ضربدر احتمال پذیرش آن(از یاد نبرید که درصورت رد پیشنهاد، پیشنهاددهنده چیزی بدست نخواهد آورد).در اینجا میبینیم که پاسخگو چگونه بازدهیهای انتظاری پیشنهاد ۴۰ درصد و ۳۰ درصد را محاسبه میکند:
البته نمیتوانیم بدانیم که آیا کشاورزان واقعا درگیر چنین محاسباتی میشوند یا نه. اما اگر بشوند، بایستی به این نتیجه رسیده باشند که طرح پیشنهاد ۴۰ درصد بازدهی انتظاری آنها را به حداکثر میرساند. این انگیزه مغایر است با مورد پیشنهادهای پذیرفتنی، که درآن ملاحظاتی از این قبیل در کار بود: مخالفت با نابرابری، همـنفعخواهی، یا میل به توسل به هنجاری اجتماعی. برخلاف پاسخگویان، بسیاری از پیشنهاددهندگان ممکن است سعی خود را در بدست آوردن حداکثری پول در آزمایش بهخرج داده باشند و کنشهای پاسخگویان را[ هم اتفاقا] درست حدس زده باشند.
محاسبات مشابه نشان میدهند که، در میان دانشجویان، پیشنهادی که بازدهی انتظاری حداکثری را در پی داشت ۳ درصد بود، و این معمولترین پیشنهاد در میان آنها بود. پیشنهادهای پایینتر دانشجویان میتوانست یه این خاطر باشد که آنها بهدرستی پیشبینی کرده بودند که پیشنهادهای دست پایین( حتی به پایینی ۱۰ درصد) هم گاهی با پذیرش مواجه خواهند شد. آنها ممکن است برای به حداکثر رساندن بازدهی تلاش میکردهاند و امیدوار بودهاند که بتوانند از مجازات طرح پیشنهادهای پایین قسر در روند.
تمرین ۴.۹ پیشنهادها در بازی التیماتوم
- بهنظر شما چرا بعضی از کشاورزان بیش از ۴۰ درصد پیشنهاد دادهاند؟ چرا برخی دانشجویان پیشنهاد بالای ۳۰ درصد مطرح کردهاند؟
- چرا برخی کمتر از این پیشنهاد دادند؟
- کدامیک از تمایلات اجتماعی مورد مطالعهی شما ممکن است در این امر دخیل بوده باشد؟
وجوه تمایز این دو جمعیت در چیست؟ هرچندکه بسیاری کشاورزان و دانشجویان مبلغی را پیشنهاد دادند که بازدهی انتظاری آنها را به حداکثر برساند، اما شباهت در همین نقطه متوقف میشود. کشاورزان کنیایی به احتمال بیشتری پیشنهادهای پایین را رد میکردند. آیا این دال بر تفاوتی میان آمریکاییها و کنیاییها، یا کشاورزان و دانشجویان است؟ یا نه چیزی است مربوط به هنجارهای اجتماعی بومی، و نه ملیت و شغل؟ آزمایشها به تنهایی قادر به پاسخگویی به این سؤالات جالب نیستند، اما پیش از آنکه نتیجه بگیرید که کشاورزان کنیایی بیشتر از آمریکاییها مخالف نابرابری هستند، شاید جالب باشد بدانید که همین آزمایش میان روستاییهای ایالت میسوری در ایالات متحده انجام شد، و حتی احتمال رد پیشنهادهای پایین در میان آنها بیشتر از کشاورزان کنیایی بود. تقریبا همهی پیشنهاددهندگان میسوریایی پیشنهادی معادل نصف کلوچه را مطرح کردند.
پرسش ۴.۱۰ (یکی از پاسخها را انتخاب کنید)
بازیِ التیماتومی را در نظر بگیرید که در آن پیشنهاددهنده یک سهمِ ۱۰۰ دلاری را به پاسخگو پیشنهاد میکند. پاسخگو میتواند پیشنهاد را رد کرده یا بپذیرد. اگر بپذیرد، هر دو سهمِ مقرر را میگیرند، حالآنکه اگر پیشنهاد را رد کند، هیچیک چیزی گیرشان نخواهد آمد. شکل ۴.۱۲ نتایجِ یک مطالعه را نشان میدهد که پاسخهایِ دانشجویانِ دانشگاهِ آمریکایی و کشاورزانِ کنیایی را با یکدیگر مقایسه میکند.
با توجه به این اطلاعات می توان چنین نتیجه گرفت:
- کشاورزانِ کنیایی در آزمایشِ فوقالذکر با احتمالِ بیشتری نسبت به دانشجویانِ آمریکایی، پیشنهادهایِ پایین را رد میکنند. این به آن معنا نیست که همهیِ کنیاییها، در قیاس با آمریکاییها، تمایلِ بیشتری به ردِّ پیشنهادهایِ پایین دارند.
- درست ۵۰% کشاورزانِ کنیایی پیشنهادی را رد کردند که براساسِ آن پیشنهاددهنده ۳۰% دریافت میکرد.
- هر دو گروهِ پاسخگویان پیشنهادِ صفر را به شکلی ۱۰۰ درصدی رد کردند.
- این واقعیت که کشاورزانِ کنیایی به احتمالِ زیاد پیشنهادهایِ غیرمنصفانه را رد کردهاند و بر هرگونه درآمدی چشم پوشیدهاند، نشانگرِ آن است که آنها برایِ برابری و انصاف ارزشِ بیشتری قائل هستند.
پرسش ۴.۱۱ (یکی از پاسخها را انتخاب کنید)
جدولِ زیر درصدِ پاسخگویانی را نشان میدهد که، در آزمایشِ انجام شده با کشاورزانِ کنیایی و دانشجویانِ آمریکایی، مبلغِ پیشنهادی در بازیِ التیماتوم را رد کردهاند. کلوچه معادلِ ۱۰۰ دلار است.
| مبلغِ پیشنهادی | صفر دلار | ۱۰ دلار | ۲۰ دلار | ۳۰ دلار | ۴۰ دلار | ۵۰ دلار | |
|---|---|---|---|---|---|---|---|
| سهمِ رد شده | کشاورزانِ کنیایی | ۱۰۰٪ | ۱۰۰٪ | ۹۰٪ | ۴۸٪ | ۴٪ | صفر٪ |
| دانشجویانِ آمریکایی | ۱۰۰٪ | ۴۰٪ | ۳۵٪ | ۱۵٪ | ۱۰٪ | صفر ٪ |
عطف به این اطلاعات میتوان گفت که:
- بازدهیِ انتظاری، بختِ ۸۵ درصدیِ نگهداشتِ ۷۰ دلار است: ۰.۸۵ * ۷۰=۵۹.۵۰ .
- بازدهیِ انتظاری، بختِ ۹۰ درصدیِ نگهداشتِ ۶۰ دلار است: ۰.۹۰ * ۶۰= ۵۴ .
- بازدهیِ انتظاری، بختِ ۱۰ درصدیِ نگهداشتِ ۸۰ دلار است: ۰.۱۰ * ۸۰= ۸ .
- احتمالِ مواجهه با ردِّ پیشنهاد برایِ کشاورزانِ کنیایی بالاتر از دانشجویانِ آمریکایی است. ازاینرو بازدهیِ انتظاریِ کشاورزان پایینتر است.
تمرین ۴.۱۰ اعتصابها و بازی اولتیماتوم
اعتصاب علیه دستمزد یا شرایط کاری را میتوان نمونهی یک بازی التیماتوم دانست.
- برای الگوسازی یک اعتصاب درقالب یک بازی اولتیماتوم، چه کسی پیشنهاددهنده و چه کسی پاسخگو است؟
- برای ارائهی وضعیت یک درخت بازی بکشید.
- یک اعتصاب مشهور را در نظر بگیرید و توضیح دهید که چگونه با تعریف یک بازی اولتیماتوم خوانایی دارد؟
- در این بخش دادههای آزمایشگاهی در اختیار شما گذاشته شد تا پیشبینیهای بازی التیماتوم را به بوتهی آزمون بگذارید. براساس دادهها چگونه میتوانید نشان دهید که چه نوع وضعیتی به اعتصاب منجر میشود؟
۴.۱۲ رقابت در بازی التیماتوم
بازیهای التیماتوم دونفره نشان میدهد که مردم چگونه ممکن است بخواهند نفع پدیدار شده در اثنای یک تعامل اقتصادی را تقسیم کنند. اما خروجی یک مذاکره، اگر تحت تاثیر رقابت باشد، میتواند متفاوت باشد. برای مثال، استادی که پی یک دستیار میگردد، میتوانست بهجای یکی،چند تا دستیار انتخاب کند.
نسخهی جدیدی از بازی التیماتوم را تصور کنید که در آن پیشنهاددهندهای بهجای یک نفر به دو پاسخگو پیشنهاد دوطرفهی ۱۰۰ دلاری را ارائه میکند. اگر یکی از پاسخگویان بپذیرد و دیگری نه، آنوقت پاسخگوی مذکور و پیشنهاددهنده سهم میبرند و پاسخگوی دیگر چیزی بدست نمیآورد. اگر هیچیک نپذیرند، هیچیک، منجمله پیشنهاددهنده چیزی بدست نمیآورند. اگر هر دو پاسخگو بپذیرند، یکی از آنها بهشکلی تصادفی انتخاب میشود و سهم را میگیرد.
اگر شما یکی از پاسخگویان باشید، کمینه پیشنهادی که میپذیرید چقدر خواهد بود؟ آیا در مقایسه با بازی التیماتوم اصلی که یک پاسخگو دارد، تفاوتی در پاسخهای شما دیده میشود؟ شاید. اگر من بدانم که رقیب من بشدت تحت تاثیر هنجارهای تقسیم ۵۰-۵۰ است، درآنصورت تفاوت چندانی در پاسخ من وجود نخواهد داشت. اما اگر بهزعم من رقیب من بشدت خواهان تمامی پاداش باشد، و اهمیت چندانی به منصفانه بودن پیشنهاد ندهد چه؟
و حالا فرض کنید که شما پیشنهاددهنده هستید. چه سهمی را پیشنهاد خواهید کرد؟
شکل ۴.۱۴ شواهدی آزمایشگاهی را برای گروه بزرگی از سوژهها را نشان میدهد که دارند راندهای چندگانهی بازی را پیش میبرند. پبشنهاددهندگان و پاسخگویان بهنحو تصادفی و ناشناس در هر راند با یکدیگر روبرو شدند.
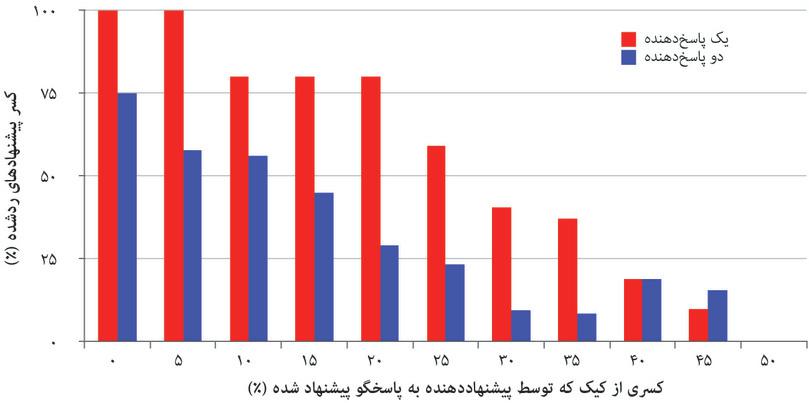
سهم پیشنهادهای رد شده در بازی التیماتوم، برحسب اندازهی پیشنهاد و تعداد پاسخگویان.
شکل ۴.۱۴ سهم پیشنهادهای رد شده در بازی التیماتوم، برحسب اندازهی پیشنهاد و تعداد پاسخگویان.
Adapted from Figure 6 in Urs Fischbacher, Christina M. Fong, and Ernst Fehr. 2009. ‘Fairness, Errors and the Power of Competition’. Journal of Economic Behavior & Organization 72 (1): pp. 527–45.
میلههای قرمز سهم پیشنهادات رد شده را در مواقعی نشان میدهند که یک پاسخگو وجود دارد. میلههای آبی اتفاقات رویداده با دو پاسخگو را نشان میدهند. وقتی رقابتی جاری باشد، احتمال اینکه پاسخگویان پیشنهادهای پایین را رد کنند کمتر است: رفتار آنها بیشتر به رفتار افراد خودمنفعتطلبی شباهت دارد که بیشتر نگران بازدهی پولی خودشان هستند.
برای تبیین این پدیده برای خود، به این بیاندیشید که وقتی پاسخگویی پیشنهاد پایینی را رد میکند: معنای آن رسیدن او به بازدهی صفر است. علیرغم موقعیتی که در آن یک پاسخگوی تنها وجود دارد، پاسخگو در یک وضعیت رقابتی نمیتواند از مجازات پیشنهاددهنده مطمئن باشد، چراکه آن پاسخگوی دیگر ممکن است پیشنهاد پایین را بپذیرد( چرا که افراد در مواجهه با پیشنهادها از هنجارهای یکسانی برخوردار نیستند، یا سطح نیازهای آنان مشابه نیست).
در نتیجه، حتی مردمی که گرایش به انصاف و برابری دارند هم پیشنهادهای پایین را به هدف اهتراز از بدترین شرایط ممکنه میپذیرند. البته، پیشنهاددهندگان هم این را میدانند، لذا پیشنهادهای پایینتری مطرح میکنند، پیشنهادهایی که پاسخگویان کماکان میپذیرند. توجه داشته باشید که چگونه یک تغییر کوچک در قوانین یا در وضعیت میتواند تاثیر بزرگی بر خروجی بگذارد. تغییر در قوانین بازی از اهمیت برخوردار است، بههمان ترتیب که در بازی کالای عمومی دیدیم که اضافه کردن گزینهای برای مجازات مفتسواران سطوح همکاری را افزایش داد.
تمرین ۴.۱۱ تنگنای زندانی ترتیبی
برگردیم به تنگنای زندانی کنترل آفَت که بالا و آنیل بازی میکردند شکل ۴.۳ب، اما اینبار فرض کنید که بازی، همانند بازی التیماتوم، بهشکل ترتیبی برگزار میشود. ابتدا یک بازیکنـ که بهشکل تصادفی انتخاب شدهـ یک استراتژی را برمیگزیند( عامل اول)، و بعد دیگری حرکت میکند(عامل دوم).
- فرض کنید که شما عامل دوم باشید و عامل اول IPC را برگزیده باشد، آنوقت شما چه انتخابی خواهید کرد؟
- فرض کنید که شما عامل اول هستید و میدانید که عامل دوم برخوردار از تمابلات همـنفعخواهانهی قوی است، بهاین معنا که او درقبال کسی که هنجارهای اجتماعی را بجا میآورد کنش مهربانانهای پیش خواهد گرفت، آنوقت چه میکنید؟
۴.۱۳ تعاملات اجتماعی: تضاد در انتخاب میان توازنهای نش
در بازی دست نامرئی، تنگنای زندانی، و بازی کالای عمومی، کنشی که بالاترین بازدهی را برای بازیکن در پی داشت، به کنش بازیکن دیگر بستگی نداشت: برای هر بازیکنی یک استراتژی مسلط وجود داشت، و بازی بههمین خاطر فقط یک توازن استراتژی مسلط داشت.
اما اغلب وضع بهاین ترتیب نیست.
- توازن نش
- مجموعه ای از استراتژیها، یعنی یک استراتژی به ازای هر بازیگر، بطوریکه استراتژی هر بازیگر بهترین پاسخ به استراتژیهای منتخب همه افراد دیگر باشد.
در ایالات متحده، هر کسی که در سمت راست رانندگی میکند یک توازن است، بدان معنا که هیجکس با درنظرگیرفتن آنچه دیگران انجام میدهند، تمایلی به تغییر استراتژی خود ندارد. در نظریهی بازی، درصورتیکه هرکس بهترین پاسخ خود به استراتژیهای هرکس دیگری را بازی کند، استراتژیهای مذکور را توازن نش مینامند.
اما در ژاپن هرکس از چپ براند، یک توازن نش است. بازی رانندگی برخوردار از دو توازن نش است.
بسیاری از کنشهای متقابل اقتصادی توازنهای استراتژی مسلط ندارند، اما اگر بتوانیم یک توازن نش بیابیم، یک پیشبینی از آنچه باید مشاهده کنیم را دراختیارمان میگذارد: باید انتظار دیدن آنرا داشته باشیم که همهی بازیکنان، باتوجه به کنشهای دیگران، تا سرحد ممکن تلاش میکنند.
اما حتی در مسائل سادهی اقتصادی هم ممکن است بیش از یک توازن نش داشته باشیم(چنانکه در بازی رانندگی اینطور بود). فرض کنید زمانی که بالا و آنیل محصول خود را انتخاب میکنند، بازدهیها آنگونه باشد که در شکل ۴.۱۵. آمده است. این متفاوت از بازی دست نامرئی است: اگر دو کشاورز محصول مشابهی تولید کنند، اکنون چنان افت قیمتی بوجود آمده که بهتر است هریک زمینش را به کشت یک محصول ویژه اختصاص دهند، حتی اگر محصولی باشد که مناسب کشت در زمینشان نیست. از خطوط جانبی برای یافتن دو توازن استفاده کنید.
وضعیتهای با دو توازن نش، ما را به طرح دو ؤال بر میانگیزد:
- در جهان انتظار مشاهدهی کدامیک از این توازنها را داریم؟
- آیا اگر برخی بازیکنان توازنی را ترجیح دهند و باقی نه، این به یک تضاد منافع منجر میشود؟
مادامی که تصمیم شما درباره رانندگی با دیگر افراد مشابه باشد، دیگر اینکه شما از راست برانید یا از چپ، به خودی خود موضوع تضاد نیست. نمیتوان گفت که رانندگی در سمت چپ جاده بهتر از رانندگی در سمت راست آن است.
اما در بازی تقسیم کار، مبرهن است که دو کشاورز از [بین دو توازن نش] آن توازنی را ترجیح میدهند که در آن آنیل کاساوا و بالا برنج را برگزیدهاند( آنجا که هریک محصول متفاوت و ویژهای را برای تولید انتخاب کردهاند).
پس آیا میتوان چنین گفت که انتظار ما این است که ببینیم آنیل و بالا درگیر یک تقسیم کار درست شدهاند؟. نه لزوما! بیاد داشته باشید که، فرض ما این است که آنها تصمیماتشان را مستقلانه و بدون هماهنگی میگیرند. تصور کنید که پدر بالا بهشکل ویژه در کاشت کاساوا مهارت دارد(برخلاف پسرش) و ازاینرو زمین به کشت کاساوا اختصاص خواهد یافت، حتی اگر خاکش بیشتر مناسب برنج باشد. در واکنش به این، آنیل میداند که برنج، بهترین پاسخ او با کاساوای بالا است، و بههمین دلیل برنج را برای کاشت انتخاب خواهد کرد. [در چنین وضعیتی]بالا هیچ مشوق و انگیزهای برای رویگردانی به سمت تخصص خود ندارد: کاشتن برنج.
مثال فوق دربردارندهی نکتهی مهمی است: اگر بیش از یک توازن نش در کار باشد، و اگر مردم کنش خود را مستقلانه انتخاب کنند، آنوقت یک اقتصاد میتواند در یک توازن نش «گیر بیافتد» که درآن همهی بازیکنان، در قیاس با آن توازن دیگر،به وضع وخیمتری دچار میشوند.
اقتصاددانان بزرگ جان نش
جان نش (۱۹۲۸-۲۰۱۵) تز دکترای خود را در دانشگاه پرینستون و در سن ۲۱ به اتمام رساند این تز فقط ۲۷ صفحه است:، و بااینهمه این تز نظریهی بازی را (که تا پیش از این شاخهی مهجوری از ریاضیات بود) بهگونهای بسط داد که به دگرگونی چشمگیری در علم اقتصاد انجامید. وی پاسخی برای یک پرسش بدست آورده بود: وقتی مردم بهنحو استراتژیکی درگیر تعامل میشوند، انتظار چه کاری از آنها میرود؟ پاسخ او، که اکنون به توازن نش، مشهور است، مجموعهای از استراتژیهاست، هریک ازآن بازیکنی، بهگونهای که اگر این استراتژیها را به استحضار عموم برسانیم، هیچ بازیکنی از انتخاب خود متاسف نباشد. بدین معنا که، اگر همهی بازیکنان استراتژیهای مطابق با یک توازن نش را انتخاب کرده باشند، دیگر هیچکس نمیتواند با چرخش یکجانبه به سوی یک استراتژی متفاوت دیگر نفع ببرد. کار نش از معرفی صِرف مفهوم یک توازن بسی فراتر میرود. او ثابت کرد که چنین توازنی تحت شرایط بسیار عام وجود دارد، و مستلزم آن است که بازیکنان مجاز به انتخاب تصادفی از میان مجموعه استراتژیهایی باشد که در دسترس او هستند. برای درک اهمیت این نکته، یک بازی کودکانهی دونفرهی سنگـکاغذـقیچی را درنظر بگیرید. اگر هر یک از بازیکنان یکی از سه استراتژی موجود را با اطمینان انتخاب کند، آنوقت حداقل یکی از بازیکنان از باخت خود مطمئن خواهد بود و بنابراین به نفع او خواهد بود که استراتژی متفاوتی را برگزیند. اما اگر هر دو بازیکن هر استراتژی دم دست را به احتمال مساوی انتخاب کنند، آنوقت هیجیک قادر نخواهد بود با انتخاب تصادفی استراتژیها بهشیوهای متفاوت، کنش بهتری انجام دهد. در نتیجه این یک توازن نش است.
آنچه نش قادر به اثبات آن بود، اینست که هرگونه بازی با شمار محدودی بازیکن، که هریک از آنها برخوردار از شمار محدودی استراتژی است، حداقل بایستی یک توازن داشته باشد، مشروط بر اینکه بازیکنان بتوانند آزادانه و بهشکلی تصادفی استراتژیها را برگزینند. این یافتهای کارآمد است زیرا استراتژیها ممکن است ابژههای بسیار پیچیدهای باشند، که دربردارندهی برنامهی کاملی است، که مشخص میکند در هر وضعیت مفروضی، چه کنشی باید اختیار شود. برای نمونه، تعداد استراتژیهای ثابت در شطرنج بیشتر از تعداد اتمهای شناختهشده در جهان است. اما هنوز ما میدانیم که شطرنج دارای یک توازن نش است، البته اینکه آیا توازن مذکور مستلزم برد سفید، برد سیاه، یا تساوی تضمین شده است، همچنان بر ما نامعلوم میماند.
نکتهی شایان توجه دررابطه با اثبات وجود توازن نش این است که اغلب ریاضیدانان ممتاز قرن بیستم، منجمله امیل بورِل و جان ون نیومن، مساله را بدون بررسی کافی زیر سؤال بردند. آنها تنها میتوانستند برای بازیهای صفرـجمع مشخص وجود توازن را نشان دهند؛ بازیهایی که درآنها سود یک بازیکن همسنگ خسارت دیگران است. این امر بوضوح ظرف نظری آنها برای اقدامات اقتصادی را محدود کرد. نش به طبقهی بسیار عامتری از بازی مجال بروز داد که درآن بازیکنان میتوانند هر هدفی داشته باشند: میتوانند برای نمونه، خودخواه باشند، دیگرخواه باشند، دست و دلباز باشند، یا تمایل به برابری و انصاف داشته باشند.
بهسختی بتوان حوزهای در اقتصاد یافت که پیشرفت نظریهی بازی آن را بکلی دگرگون نکرده باشد، و این پیشرفت بدون برهان مفهوم و وجود توازن نش ممکن نمیبود. قابل ملاحظه است که این تنها کمک خطشکنانهی نش به اقتصاد نبوده است ـ وی همچنین سهم برجسته و بدیعی در نظریهی چانهزنی دارد. افزون بر این، در دیگر حوزههای ریاضی پیشگام بوده و بخاطر آن جایزهی افتخاری آبل را به او اعطا کردهاند.
نش احتمالا بخاطر کارش جایزهی نوبل را هم دریافت کند. راجر مایرسن، اقتصاددانی که او نیز جایزه نوبل را برده، توازن نش را «یکی از مهمترین دستاوردهای تاریخ تفکر اقتصادی» میداند.
نش در اصل میخواست مثل پدرش یک مهندس برق بشود،و در بنیاد کارنگی تِک که اکنون دانشگاه کارنگی ملون نام دارد لیسانس ریاضیات گرفت. یک درس عمومی در موضوع اقتصاد بینالملل علاقهی او به کنشهای متقابل استراتژیک را برانگیخت، که اتفاقا به کشف بزرگش منجر شد.16
نش بخش اعظم زندگیش را از یک بیماری روانی رنج برد که مستلزم بستری شدناش بود. وی به علت شیزوفرنی ای که در ۱۹۵۹ بدان دچار شد، دچار توهماتی میشد، البته بهدنبال آنچه خود «۲۵ سال اندیشهی وهمی» میخواند به تدریس و پژوهش در پرینستون ادامه داد. داستان بصیرتها و بیماری او در کتاب ذهن زیبا آمده است و فیلمی با بازی راسل کرو نیز ازآن ساخته شده است.
حل و فصل تضاد
تضاد منافع زمانی رخ میدهد که بازیکنان در یک بازی توازنهای نش متفاوتی را ترجیح دهند.
برای فهم موضوع، مورد آسترید و بتینا را درنظر بگیرید، دو مهندس نرمافزار که بر روی پروژهای کار میکنند و قرار است بابت آن دستمزد بگیرند. تصمیم اول آنها مربوط است به اینکه آیا برای نوشتن رمزها از جاوا استفاده کنند یا از زبان C++( فرض کنید که هر دو زبان برنامهنویسی به یکسان مناسب هستند و اینکه میتوان بخشی از پروژه را با یک زبان و بخشی را به زبان دیگر نوشت). هر یک از آنها مجبور به انتخاب این یا آن برنامه هستند، اما آسترید میخواهد به جاوا بنویسد زیرا در نوشتن رمزهای جاوا ماهرتر است. از آنجایی که این یک پروژهی مشترک با بتینا است، دستمزد او تاحدی به تعداد سطرهای کدهای نوشتهشده توسط او متکی است. متاسفانه بتینا دقیقا به دلیلی مشابه C++ را ترجیح میدهد. بااین تفاسیر دو استراتژی را استراتژی جاوا و C++مینامیم.
تعامل آنها در شکل ۴.۱۶الف، توصیف شده است و بازدهیهای آنها در شکل ۴.۱۶ب آمده است.
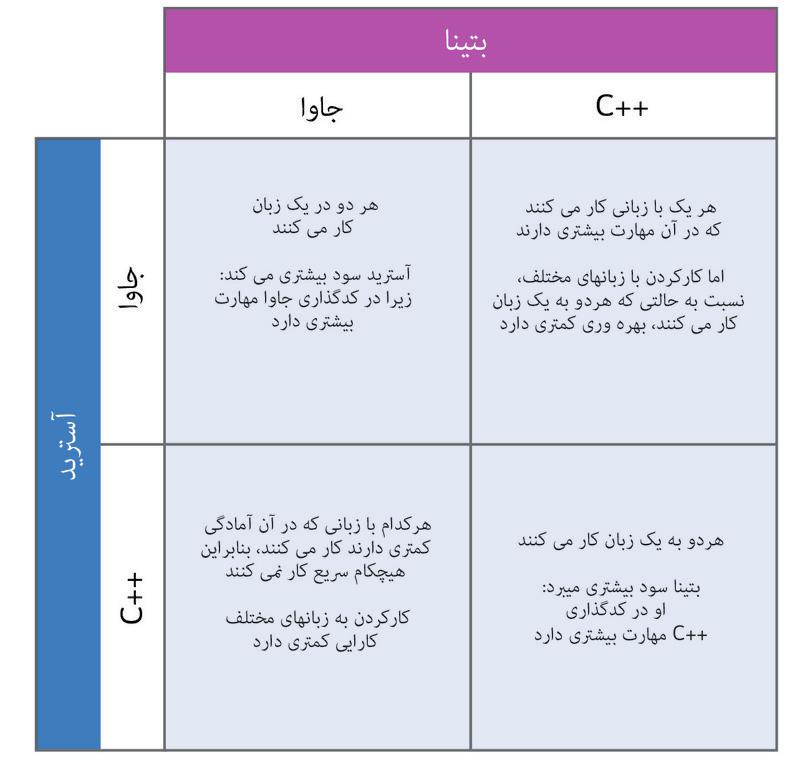
کنشهای متقابل در انتخاب زبان برنامهنویسی
شکل ۴.۱۶الف کنشهای متقابل در انتخاب زبان برنامهنویسی
از شکل ۴.۱۶الف، میتوان نتایج زیر را بیرون کشید:
- اگر هر دو به زبان یکسانی کار کنند، نتیجهی بهتری میگیرند.
- به نفع آسترید است اگر آن زبان جاوا باشد، حالآنکه عکس آن برای بتینا صادق است.
- بازدهی کل آنها درصورت انتخاب C++ بالاتر میرود.
خروجی این بازی را چگونه پیشبینی خواهیم کرد؟
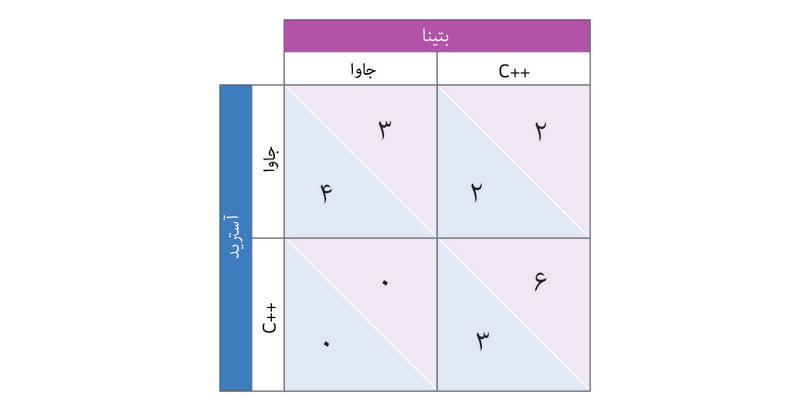
بازدهیهای (هزاران دلار برای تکمیل پروژه) برحسب انتخاب زبان برنامهنویسی.
شکل ۴.۱۶ب بازدهیهای (هزاران دلار برای تکمیل پروژه) برحسب انتخاب زبان برنامهنویسی.
با بکار بردن روش نقطهـوـدایره درخواهید یافت که بهترین پاسخ هر بازیکنی انتخاب زبانی یکسان با بازیکن دیگر است. لذا دو توازن نش وجود دارد: یکی که درآن هر دو جاوا را انتخاب میکنند، و یکی دیگر که درآن هر دو C++ را انتخاب میکنند.
آیا میتوانیم بگوییم که احتمال روی دادن کدامیک از این دو توازن بیشتر است؟ آسترید بهوضوح تمایل دارد که هر دو جاوا را بازی کنند، درحالیکه ترجیح بتینا این است که هر دو C++ را بازی کنند. با اطلاعاتی که دربارهی چگونگی تعامل ایندو داریم، هنوز نمیتوانیم پیشبینی کنیم که چه اتفاقی خواهد افتاد. تمرین ۴.۱۲ مثالهایی از نوع اطلاعاتی در اختیارمان میگذارد که کمک میکند مشاهداتمان را توضیح دهیم.
تمرین ۴.۱۲ تضاد بین آسترید و بتینا
نتیجهی احتمالی این بازی شکل ۴.۱۶ب چیست اگر:
- آسترید بتواند انتخاب کند که کدام زبان را اول بکار گیرد، و به آن مبادرت کند( درست مثل پیشنهاددهندهای که در بازی التیماتوم، پیش از پاسخ پاسخگو مبادرت به طرح پیشنهاد میکند)؟
- هردو توافقی حاصل میکنند، دررابطه بااینکه چه زبانی را بکار گیرند، و اینکه اندازهی انتقال مالی از یکی به دیگری چقدر باشد؟
- سالهای سال با یکدیگر کار میکردهاند، و اگر در گذشته در پروژههای مشترک جاوا را بکار گرفته باشند؟
تمرین ۴.۱۳ تضاد در تجارت
در دههی ۱۹۹۰ شرکت مایکروسافت و شرکت نتاسکِیپ بر سر سهم بازار برای جستجوگرهای اینترنتی شان، موسوم به اینترنت اکسپلورر و نویگیتور وارد نزاع شدند. در دههی ۲۰۰۰، گوگل و یاهو بر سر اینکه موتور جستجوگر کدام شرکت باید بیشتر مورد استفادهی عموم واقع شود. در صنعت آزمایش نزاعی با عنوان «جنگ فرمتها» میان Blu-Ray و HD-DVD در گرفت.
با استفاده از این مثالها تحلیل کنید که آیا توازنهای چندگانه در آن وجود دارد یا نه، و اگر هست، چرا یک توازن خاص ممکن است بهجای دیگر توازنها پدیدار شود.
پرسش ۴.۱۲ ( یک پاسخ را انتخاب کنید)
ماتریسِ بازدهیِ زیر برایِ یک بازیِ یک نوبته همزمان را درنظر بگیرید که درآن بالا و آنیل محصولاتِ خود را انتخاب میکنند.
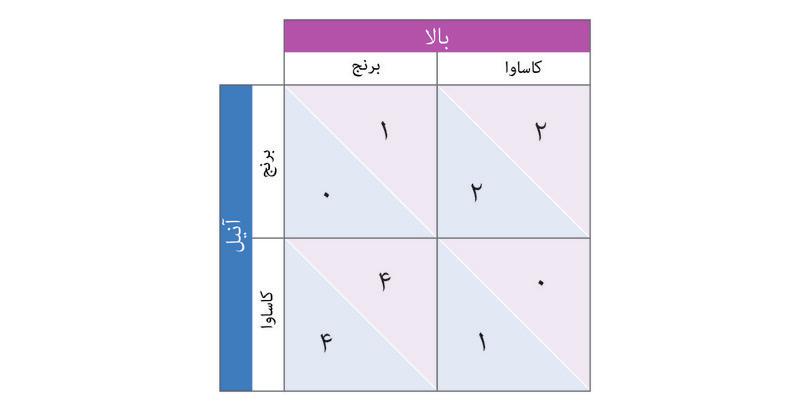
میتوانیم نتیجه بگیریم که:
- در این دو مورد، هم آنیل و هم بالا بهترین پاسخِ خود به استراتژیِ فردِ دیگر را بازی میکنند. بنابراین، این جفت استراتژی توازنهایِ ناش هستند.
- وقتی بالا کاساوا را انتخاب میکند، آنیل بهتر است که برنج را انتخاب کند. ازاینرو کاساوا برایِ آنیل استراتژیِ مسلط نیست.
- وقتی آنیل برنج را انتخاب میکند، برایِ بالا بهتر است که کاساوا را کنار بگذارد. ازاینرو برنج برایِ بالا استراتژیِ مسلط نیست.
- هیچگونه استراتژیِ مسلطی وجود ندارد. پس هیچ توازنِ استراتژیِ مسلطی هم وجود ندارد.
تمرین ۴.۱۴ توازن نش و تغییرات اقلیمی
مسالهی تغییر اقلیم را بهعنوان یک بازی بین دو کشور با نامهای چین و ایالات متحده در نظر بگیرید، انگارکه هر یک فرد منفردی باشند. هر کشوری برای ارجاع به انتشار جهانی کربن دو استراتژی ممکن دارد: تحدید (اتخاذ روشهایی برای کاهش انتشار، برای مثال با وضع مالیات بر استفاده از سوختهای فسیلی)، و BAU ( گزارش استرن از تجارت بهعنوان سناریوی همیشگی). شکل ۴.۱۷ خروجیها و بازدهیهای فرضی را، روی طیفی از بهترین، تا خوب و بد و بدترین، توصیف میکند. چنین مقیاسی را مقیاس ترتیبی مینامند( زیرا تنها چیزی که در آن موضوعیت دارد ترتیب است): آیا یک خروجی خاص بهتر از دیگری است یا نه، اینجا شدت این بهتر بودن مهم نیست.
![سیاست تغییرات اقلیمی بهمثابهی تنگنای زندانی(بالا). بازدهیها برای سیاست تغییرات اقلیمی بهمثابهی یک تنگنای زندانی(زیر چپ)، بازدهیها برای سیاست تغییرات اقلیمی همراه با مخالفت با نابرابری و همـنفعخواهی(زیر راست).]()
![سیاست تغییرات اقلیمی بهمثابهی تنگنای زندانی(بالا). بازدهیها برای سیاست تغییرات اقلیمی بهمثابهی یک تنگنای زندانی(زیر چپ)، بازدهیها برای سیاست تغییرات اقلیمی همراه با مخالفت با نابرابری و همـنفعخواهی(زیر راست).]()
![سیاست تغییرات اقلیمی بهمثابهی تنگنای زندانی(بالا). بازدهیها برای سیاست تغییرات اقلیمی بهمثابهی یک تنگنای زندانی(زیر چپ)، بازدهیها برای سیاست تغییرات اقلیمی همراه با مخالفت با نابرابری و همـنفعخواهی(زیر راست).]()
شکل ۴.۱۷ سیاست تغییرات اقلیمی بهمثابهی تنگنای زندانی(بالا). بازدهیها برای سیاست تغییرات اقلیمی بهمثابهی یک تنگنای زندانی(زیر چپ)، بازدهیها برای سیاست تغییرات اقلیمی همراه با مخالفت با نابرابری و همـنفعخواهی(زیر راست).
- برای هر دو کشور خروجی بهتری حاصل میشد اگر میتوانستند بر سر یک معاهدهی الزامآور برای محدود کردن انتشار به توافق برسند. چرا رسیدن به این توافق ممکن است دشوار باشد؟
- توضیح دهید که بازدهیهای شکل ۴.۱۷ چگونه میتواند وضعیتی را بازنمایی کند که درآن هر دو کشور مخالف نابرابری هستند و همـنفعخواهی آنها را برمیانگیزد. نشان دهید که در این وضعیت دو توازن نش وجود دارد. آیا در این مورد مذاکره برای رسیدن به یک معاهده آسانتر خواهد بود؟
- تغییرات پیش آمده در تمایلات یا در جنبهی دیگری از مساله را شرح دهید، [تغییراتی] که بازی را به سمتی برمیگرداند( همچون بازی دست نامرئی) که درآن انتخاب تحدید از جانب دو کشور یک توازن استراتژی مسلط است.
۴.۱۴ نتیجه
ما نظریهی بازی را برای الگوسازی از کنشهای متقابل اجتماعی بکار گرفتهایم. بازی دست نامرئی روشن میکند که بازارها چگونه ممکن است خودـمنفعتطلبی فردی را بهگونهای هدایت کند که نفع دوجانبه حاصل شود، اما توازن استراتژی مسلط بازی تنگنای زندانی نشان میدهد که کنشهای مستقلانهی افراد چگونه میتواند با یک تنگنای اجتماعی مواجه گردد.
شواهد حاکی از آنند که افراد را صرفا خودـمنفعتطلبی برنمیانگیزد. دیگرخواهی، مجازات آشکار و برابر، و توافقات حاصل از مذاکره، همه و همه به حل تنگنای اجتماعی کمک میرسانند. ممکن است بر سر مسالهی تسهیم عواید دوجانبهی حاصل از توافق، یا بخاطر تمایل افراد به توازنهای متفاوت، تضاد منافع رخ دهد، اما هنجارها و تمایلات اجتماعیای از قبیل برابری و انصاف میتواند توافق را تسهیل کند.
مفاهیم معرفیشده در فصل ۴
پیش از اینکه به فصل بعد بروید تعاریف زیر را مرور کنید:
۴.۱۵ ارجاعات
-
Nicholas Stern. 2007. The Economics of Climate Change: The Stern Review. Cambridge: Cambridge University Press. Read the executive summary. ↩
-
IPCC. 2014. ‘Climate Change 2014: Synthesis Report’. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. Geneva, Switzerland: IPCC. ↩
-
Garrett Hardin. 1968. ‘The Tragedy of the Commons’. Science 162 (3859): pp. 1243–1248. ↩
-
Elinor Ostrom. 2008. ‘The Challenge of Common-Pool Resources’. Environment: Science and Policy for Sustainable Development 50 (4): pp. 8–21. ↩
-
Aesop. ‘Belling the Cat’. In Fables, retold by Joseph Jacobs. XVII, (1). The Harvard Classics. New York: P. F. Collier & Son, 1909–14; Bartleby.com, 2001. ↩
-
Francis Ysidro Edgeworth. 2003. Mathematical Psychics and Further Papers on Political Economy. Oxford: Oxford University Press. ↩
-
H. L. Mencken. 2006. A Little Book in C Major. New York, NY: Kessinger Publishing. ↩
-
Elinor Ostrom. 2000. ‘Collective Action and the Evolution of Social Norms’. Journal of Economic Perspectives 14 (3): pp. 137–58. ↩
-
Elinor Ostrom, James Walker, and Roy Gardner. 1992. ‘Covenants With and Without a Sword: Self-Governance is Possible’. The American Political Science Review 86 (2). ↩
-
Colin Camerer and Ernst Fehr. 2004. ‘Measuring Social Norms and Preferences Using Experimental Games: A Guide for Social Scientists’. In Foundations of Human Sociality: Economic Experiments and Ethnographic Evidence from Fifteen Small-Scale Societies, edited by Joseph Henrich, Robert Boyd, Samuel Bowles, Colin Camerer, and Herbert Gintis, Oxford: Oxford University Press. ↩ ↩2
-
Armin Falk and James J. Heckman. 2009. ‘Lab Experiments Are a Major Source of Knowledge in the Social Sciences’. Science 326 (5952): pp. 535–538. ↩
-
Joseph Henrich, Richard McElreath, Abigail Barr, Jean Ensminger, Clark Barrett, Alexander Bolyanatz, Juan Camilo Cardenas, Michael Gurven, Edwins Gwako, Natalie Henrich, Carolyn Lesorogol, Frank Marlowe, David Tracer, and John Ziker. 2006. ‘Costly Punishment Across Human Societies’. Science 312 (5781): pp. 1767–1770. ↩
-
Steven D. Levitt, and John A. List. 2007. ‘What Do Laboratory Experiments Measuring Social Preferences Reveal About the Real World?’ Journal of Economic Perspectives 21 (2): pp. 153–174. ↩
-
Samuel Bowles. 2016. The Moral Economy: Why Good Incentives Are No Substitute for Good Citizens. New Haven, CT: Yale University Press. ↩
-
Joseph Henrich, Robert Boyd, Samuel Bowles, Colin Camerer, and Herbert Gintis (editors). 2004. Foundations of Human Sociality: Economic Experiments and Ethnographic Evidence from Fifteen Small-Scale Societies. Oxford: Oxford University Press. ↩
-
Sylvia Nasar. 2011. A Beautiful Mind: The Life of Mathematical Genius and Nobel Laureate John Nash. New York, NY: Simon & Schuster. ↩

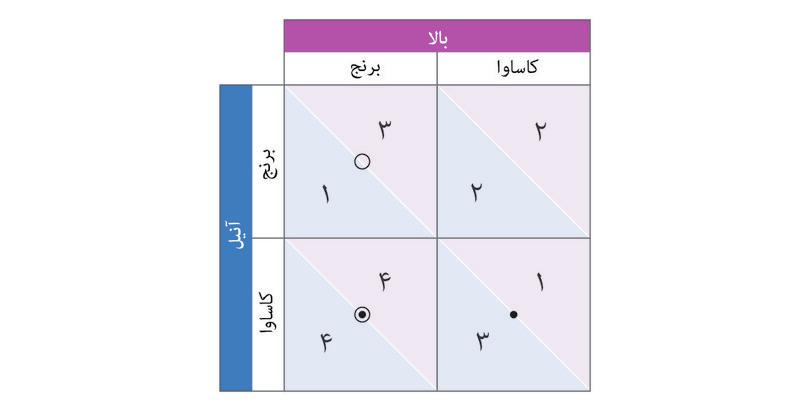
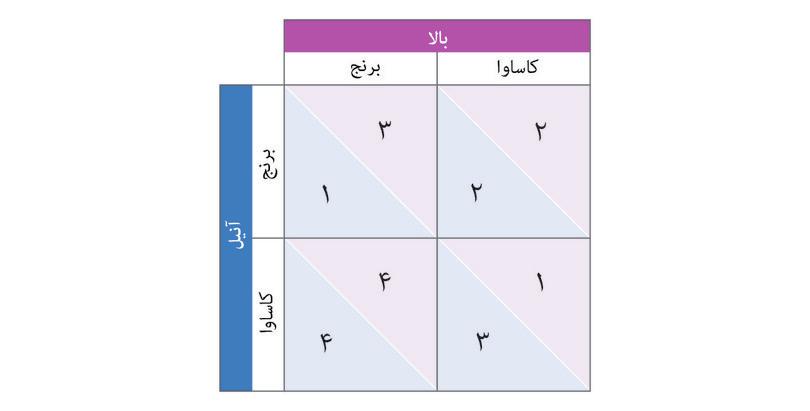
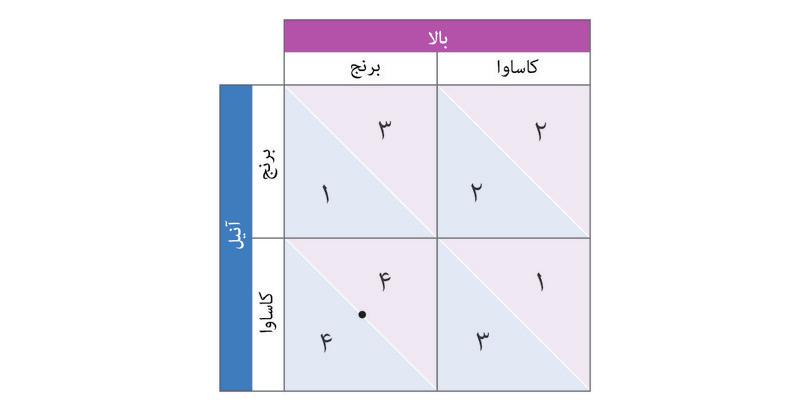
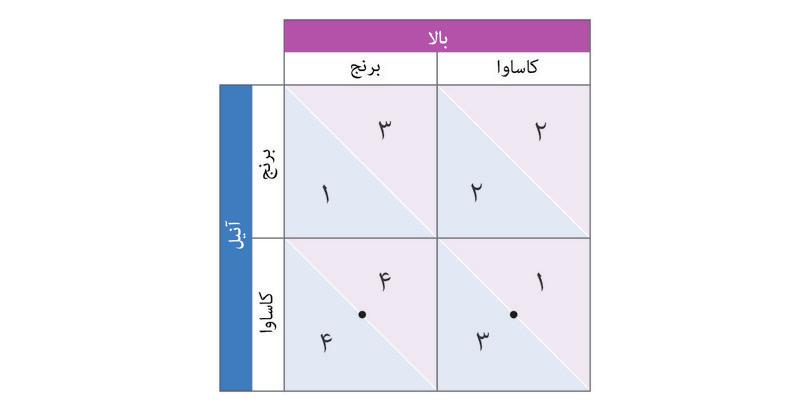
![آنیل یک استراتژی مسلط دارد
: هردوی نقطهها در ردیف پایینی جدول قرار دارند. صرفنظر از انتخاب بالا، بهترین پاسخ آنیل کاساوا است: [بهعبارتی] کاشت کاساوا استراتژی مسلط آنیل است.](../../fa/images/web/figure-04-02-b-d.jpg)